Статистический анализ уравнения регрессии

Статистический анализ уравнения регрессии начинается с проверки адекватности полученного уравнения приближенной регрессии (3.14) результатам эксперимента. В общем случае гипотеза об адекватности должна быть принята, если выполняется условие

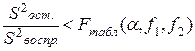, (3.19)

где 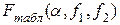– табличное значение критерия Фишера при уровне значимости 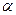и числа степеней свободы числителя f₁ и знаменателя f₂;

S²_ост – остаточное дисперсия, обусловленная влиянием неучтенных факторов и ошибками измерений в ходе проведения эксперимента;

S²_воспр. – дисперсия воспроизводимости, характеризующие рассеивание значений выходного параметра Y при повторении одного и того же опыта, при одном и том же сочетании уровней факторов.

Следует, однако, подчеркнуть, что при выполнении пассивного эксперимента, вследствие трудности повторения опытов при неизменных условиях функционирования системы, получение дисперсии воспроизводимости становится практически невозможным.

В рассматриваемых условиях для проверки адекватности целесообразно воспользоваться эмпирической зависимостью

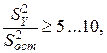(3.20)

где 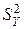– оценка дисперсии выходного параметра Y;

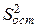– остаточная дисперсия.

Оценки дисперсии рассчитываются по следующим формулам:

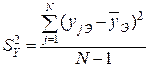, (3.21)

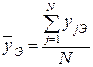, (3.22)

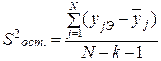, (3.23)

где 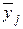– оценка выходного параметра, вычисления для j-го опыте по зависимости (3.14).

Если условие (3.20) выполняется, то гипотезу об адекватности полученного уравнения приближенной регрессии (3.14) результатам пассивного эксперимента следует принять. В противном случае, при неизменном составе входных факторов, следует выдвинуть конкурирующую гипотезу о нелинейном виде математический модели и весь процесс вычислений повторить для получения модели в виде неполного квадратного или полного квадратного полинома. Так, повышая постепенно степень полинома, можно получить в конечном итоге адекватную математическую модель.

Если по каким-то причинам проверить адекватность полученного уравнения не удалось, то следует проверить работоспособность полученной регрессивной модели, что хотя и косвенным образом, но даст некоторое представление об адекватности. Анализ работоспособности, как правило, включает в себя две основные процедуры:

1 Исследование остатков:

,

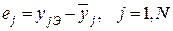то есть разностей между результатами эксперимента y_jЭ и соответствующими, предсказанными по уравнению регрессии 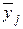. Если полученная математическая модель адекватно описывает процесс, то остатки e_j будут характеризовать свойства шума – аддитивной помехи, о законе распределения и характеристиках которой нами были приняты вполне определенные предположения (смотреть пункт 3.2.1). Таким образом, одно из основных направлений исследования остатков - это анализ справедливости исходных предположений о свойствах шума:

,

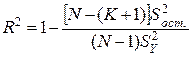который показывает, какая доля из общего рассеяния экспериментальных значений выходного параметра относительно своего среднего обусловлена регрессивной зависимостью. Величина R² может изменяться в пределах от 0 до 1. Если расчетное значение R² меньше R_min = 0,75, то уравнение регрессии можно считать неработоспособным. Если расчетное значение R² близко к единице, то можно говорить о хорошем качестве моделирования при условии, что N достаточно велико по сравнению с (К+1).

После получения адекватной модели переходят ко второму этапу статистического анализа. На данном этапе производится селекция входных факторов, суть которой заключается в следующем. На величину входного параметра системы, как правило, существенно влияет лишь часть из всей совокупности К включенных в эксперимент факторов. Тогда без особого ущерба для точности математической модели все остальные факторы можно из уравнения регрессии исключать. Для выявления незначимых факторов производится проверка значимости всех коэффициентов регрессии b_i с помощью t – критерия Стьюдента.

Факторы, для которых выполняется условие:

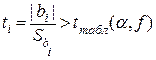, (3.24)

где t_табл. (α,f) – табличное значение критерия Стьюдента для уровня значимости α и числа степеней свободы;

f = N-K-1;

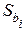– оценка среднего квадратического отклонения i-го коэффициента регрессии.

Являются значимыми, и их следует оставить в уравнении регрессии.

Величины оценок среднеквадратических отклонений коэффициентов регрессии 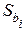можно получить умножением оценки дисперсии воспроизводимости S²_воспр. на ковариационную матрицу 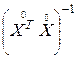, которая получается в процессе вычисления вектора коэффициентов регрессии:

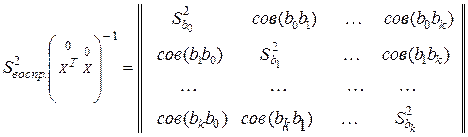. (3.25)

В матрице (3.25) элементы, лежащие на главной диагонали, есть не что иное, как оценки дисперсий соответствующих коэффициентов уравнения регрессии, а недиагональные элементы – ковариации (корреляционные моменты) соответствующих пар коэффициентов регрессии.

Ранее мы отмечали, что при проведении пассивных экспериментов, как правило, параллельные опыты не проводятся, а следовательно, дисперсия воспроизводимости S²_воспр. нам не известна.

Поэтому для вычисления матрицы (3.25) следует принять:

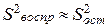
при условии, что получена адекватная математическая модель (3.14). Следует особо остановиться на процедуре исключения незначимых факторов, для которых условие (3.24) не выполняется. Исключение из полученного уравнения регрессии хотя бы одного незначимого фактора требует удаления из исходной матрицы 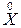входных переменных соответствующего столбца. Но так как ковариационная матрица 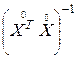при обработке результатов пассивного эксперимента не является диагональной, то исключения даже одного столбца из матрицы 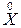повлечет за собой существенно изменение всех величин коэффициентов b_i особенно тех, которые находятся в тесной стохастической связи с коэффициентами при исключенных факторах. Следовательно, все оставшиеся коэффициенты должны быть рассчитаны заново и проведена проверка адекватности полученного уравнения регрессии. Процесс отбрасывания незначимых коэффициентов последовательно повторяется до тех пор, пока в адекватном уравнении останутся только значимые коэффициенты регрессии. Полученное таким образом уравнение приближенной регрессии вида (3.14) может быть использовано для анализа влияния входных факторов на выходной параметр исследуемой системы и для прогнозирования величин выходного параметра. В последнем случае в уравнение регрессии следует подставлять центрированные значения входных факторов 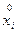. Это не всегда удобно. Поэтому целесообразно перейти к модели с нецентрированными значениями входных факторов, выполнив обратное преобразование по зависимости (3.7).

Подводя краткий итог вышеизложенному, следует отметить, что наряду с очень большим объемом вычислений, даже для сравнительно небольшого числа исследуемых входных факторов, применение регрессионного анализа для обработки результатов пассивных экспериментов редко дает интересные результаты. Это связано, прежде всего, со значительным смещением оценок выходных параметров системы вследствие воздействия на исследуемый процесс большой группы неконтролируемых факторов, которые сильно корелированы с исследуемыми факторами.