Дисперсия параметра оптимизации

Мы рассмотрели, как подсчитывается дисперсия в каждом опыте, т. е. в каждой горизонтальной строке матрицы планирования.

Матрица планирования состоит из серии опытов, и дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации 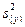, или что, то же самое, дисперсии воспроизводимости эксперимента. Вы помните, что дисперсия в каждом опыте, состоящем из n повторных наблюдений, подсчитывается по формуле

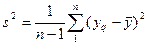. (2.1)

При подсчете дисперсии параметра оптимизации квадрат разности между значением 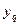в каждом опыте и средним значением из n повторных наблюдений 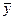нужно просуммировать по числу опытов в матрице N, а затем разделить на N (n—1), т.е.

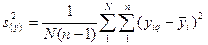, (2.2)

где i=1,2,…,N; q= 1,2,…,n.

Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице. Дисперсию воспроизводимости проще всего рассчитывать, когда соблюдается равенство числа повторных опытов во всех экспериментальных точках. На практике часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспериментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т. п.

Тогда при усреднении дисперсий приходится пользоваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы

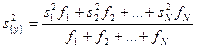, (2.3)

где 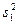— дисперсия первого опыта; 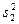— дисперсия второго опыта и т. д.; 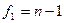— число степеней свободы в первом опыте, равное числу параллельных опытов n минус 1; 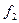— число степеней свободы во втором опыте и т. д. Число степеней свободы средней дисперсии принимается равным сумме чисел степеней свободы дисперсий, из которых она

вычислена.

Обращаем ваше внимание на то, что вы совершите ошибку, если возьмете среднее значение дисперсий без учета числа степеней свободы, а также, если возьмете среднее значение стандартных отклонений.

Стандартные отклонения нужно возвести в квадрат и затем взять взвешенное среднее, как указано выше. Случай с неравным числом наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности матрицы.

Поэтому здесь нельзя использовать расчетные формулы для коэффициентов, приведенные ранее. Этот вопрос мы рассмотрим позже, когда будем заниматься расчетом дисперсии адекватности.

Формулами для расчета дисперсии воспроизводимости эксперимента 2.2 и 2.3 можно пользоваться только в том случае, если дисперсии однородны. Последнее означает, что среди всех суммируемых дисперсий нет таких, которые бы значительно превышали все остальные. Одним из требований регрессионного анализа, с которым вы познакомитесь в следующей главе, является однородность дисперсий. Вы, конечно, понимаете, что для проверки неоднородности дисперсий нужны количественные критерии. Для того чтобы познакомиться с ними, нужно перейти к следующему параграфу.