Проверка однородности дисперсий
Проверка однородности дисперсий производится с помощью различных статистических критериев. Простейшим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с табличной величиной F-критерия.
Если полученное значение дисперсионного отношения больше приведенного в таблице для соответствующих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.
Пример 2. Пусть 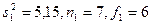 ;
; 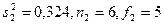 . В данном примере отношение дисперсий равно 5,14/0,324=15,9 при f1=6 и f2=5.
. В данном примере отношение дисперсий равно 5,14/0,324=15,9 при f1=6 и f2=5.
Пользуясь таблицей отношений дисперсий для различных степеней свободы и различного уровня значимости, выбираем наиболее популярный уровень значимости 0,05. В таблице по горизонтали отложены числа степеней свободы для большей дисперсии f1 а по вертикали — числа степеней свободы для меньшей дисперсии f2. Для f1=6 и f2=5 Fта6=4,40. Это значит: вероятность того, что экспериментальное значение F будет больше чем 4,40, равна 0,05 или 5%. Наше Fэксп=15,9. Оно значительно превышает табличное значение.
Так проверяется гипотеза об однородности дисперсий. Наша гипотеза состояла в том, что обе группы экспериментальных данных получены из одной и той же совокупности и дают одинаковое рассеяние. Установили, что одна дисперсия значимо отличается от другой (для выбранного уровня значимости).
Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одинаковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы по формуле 2.1, а затем из всех дисперсий находится наибольшая 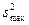 , которая делится на сумму всех дисперсий. Критерий Кохрена — это отношение максимальной дисперсии к сумме всех дисперсий:
, которая делится на сумму всех дисперсий. Критерий Кохрена — это отношение максимальной дисперсии к сумме всех дисперсий:
 .
.
С этим критерием связаны числа степеней свободы f1=n—1 и f2=N. Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превышает табличного значения. Тогда можно усреднять дисперсии и пользоваться формулой 2.1.
Пример 3. В начале главы, показывая, как нужно оформлять журнал, мы привели матрицу 2^3 с двумя повторными опытами. Мы сказали: вот с такой таблицей 4.4 можно приступать к обработке экспериментальных данных. Воспользуемся этой таблицей для расчета дисперсии воспроизводимости. Перепишем ее с целью удобства расчета (таблице 2.6).
Таблица 2.6 – Расчет дисперсии воспроизводимости
| Номер опыта | Матрица плани- рования | 
| 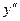
| 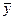
| 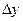
| 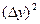
| 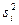
|
| (1) | 80,23 | 81,93 | 81,08 | -0,85 | 0,722 | 1,144 | |
| a | 86,50 | 84,80 | 85,65 | 0,85 | 0,722 | 1,144 | |
| b | 82,45 | 82,10 | 82,27 | 0,18 | 0,031 | 0,062 | |
| ab | 89,50 | 91,30 | 90,40 | -0,90 | 0,810 | 1,620 | |
| c | 85,10 | 84,80 | 84,95 | 0,15 | 0,023 | 0,046 | |
| ac | 90,30 | 89,60 | 89,95 | 0,35 | 0,123 | 0,246 | |
| bc | 85,60 | 84,90 | 85,25 | 0,35 | 0,123 | 0,246 | |
| abc | 88,02 | 88,48 | 88,25 | -0,23 | 0,053 | 0,106 | |
| Сумма | 2,607 |
Дисперсия в каждом опыте равна:
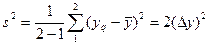 .
.
Максимальная дисперсия оказалась в опыте № 4. Экспериментальный критерий Кохрена равен 6=1,620/5,214=0,31. Табличный критерий Кохрена равен: G=0,68. Экспериментальный критерий Кохрена не превышает значения табличного. Гипотеза об однородности дисперсий подтверждается».
Дисперсия воспроизводимости равна 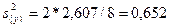 .
.
Более экономный вариант проверки однородности основан на выделении из всех дисперсий наибольшей и наименьшей. Затем по F-критерию производится проверка, значимо ли они различаются между собой. Если наибольшая и наименьшая дисперсии не отличаются значимо, то дисперсии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дисперсий можно считать принадлежащей к единой совокупности. В таких случаях нет необходимости в применении критерия Бартлета.
Если дисперсии все-таки оказались неоднородными, то оказывается полезным изменение масштаба для параметра оптимизации. При этом вводится некоторая математическая функция от параметра оптимизации, например квадратный корень или логарифм. Использование таких методов выходит за рамки элементарного анализа, и в случае необходимости экспериментатору целесообразно обращаться за советом к специалисту по планированию эксперимента.
Рандомизация
Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т. д.), рекомендуется случайная последовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random — случайный. Почему рандомизация опытов важна, покажем на следующем примере.
Пример 4. В таблице 2.7 приведена матрица 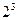 , полученная из матрицы
, полученная из матрицы 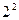 обычным способом: два раза повторен план
обычным способом: два раза повторен план 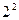 , причем в первых четырех
, причем в первых четырех
опытах x3 имеет верхнее значение, а в последних четырех опытах — нижнее
значение. Допустим, что экспериментатор может поставить в первый день
четыре опыта и во второй день также четыре опыта. Можно ли опыты ставить подряд и в первый день реализовать опыты № 1, 2, 3 и 4, а во второй — 5, 6, 7 и 8? Ставя опыты подряд, матрица разбивается на две части или на два блока: в первый блок входят опыты № 1» 2, 3 и 4, во второй — № 5, 6, 7 и 8. Если внешние условия первого дня каким-то образом отличались от внешних условий второго дня, то это способствовало возникновению некоторой систематической ошибки. Обозначим эту ошибку 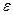 .
.
Тогда четыре значения параметра оптимизации сдвинуты на величину 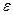 по сравнению с истинными значениями. Пусть это будут параметры, входящие в первый блок:
по сравнению с истинными значениями. Пусть это будут параметры, входящие в первый блок: 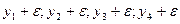 .
.
Таблица 2.7 –Матрица 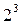 , нерандомизированная во времени
, нерандомизированная во времени
| Номер опыта | x1 | x2 | x3 | y | Номер опыта | x1 | x2 | x3 | y |
| + | + | + | y1 | + | + | - | y5 | ||
| - | - | + | y2 | - | - | - | y6 | ||
| + | - | + | y3 | + | - | - | y7 | ||
| - | + | + | y4 | - | + | - | y8 |
Однако матрица построена так, что в первом блоке значения х3 находятся на верхнем уровне, а во втором — на нижнем уровне. Тогда при подсчете b3 получится следующая картина:
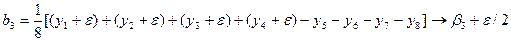 ,
,
Где 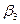 - истинное значение коэффициента при х3. Таким образом, возможное
- истинное значение коэффициента при х3. Таким образом, возможное
различие во внешних условиях смешалось с величиной линейного коэффициента b3 и исказило это значение. В такой последовательности опыты ставить нельзя. Опыты нужно рандомизировать во времени, т. е. придать последовательности опытов случайный характер.
Пример рандомизации условий эксперимента. В полном факторном эксперименте 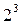 предполагается каждое значение параметра оптимизации определять по двум параллельным опытам. Нужно случайно расположить всего 16 опытов.
предполагается каждое значение параметра оптимизации определять по двум параллельным опытам. Нужно случайно расположить всего 16 опытов.
Присвоим параллельным опытам номера с 9 по 16, и тогда опыт № 9 будет повторным по отношению к первому опыту, десятый — ко второму и т. д. Следующий этап рандомизации — использование таблицы случайных чисел. Обычно таблица случайных чисел приводится в руководствах по математической статистике. В случайном месте таблицы выписываются числа с 1 по 16 с отбрасыванием чисел больше 16 и уже выписанных. В нашем случае, начиная с четвертого столбца, можно получить такую последовательность: 2; 15; 9; 5; 12; 14; 8; 7; 16; 1; 3; 13; 4; 6; 11; 10. Это значит, что первым реализуется опыт № 2, вторым — опыт № 7 и т. д. Выбранную случайным образом последовательность опытов не рекомендуется нарушать.
Дата добавления: 2021-11-16; просмотров: 740;











