Особенности расчета коэффициентов регрессии

Существенно новые возможности открылись после того, как в регрессионный анализ были привнесены идеи планирования эксперимента. Так, при ортогональном планировании матрица коэффициентов нормальных уравнений 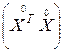становится диагональной, и ее диагональные элементы равны числу опытов N в матрице планирования. Это резко уменьшает трудности, связанные с расчетом коэффициентов уравнения регрессии. В связи с тем, что ковариационная матрица 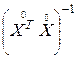также является диагональной, все коэффициенты уравнения регрессии будут некоррелированы между собой. В этом случае значимость коэффициентов можно проверять для каждого из них в отдельности и, соответственно, исключение из уравнения регрессии любого незначимого коэффициента никак не скажется на остальных. При этом коэффициенты b_i будут являться несмешанными оценками для соответствующих генеральных коэффициентов 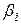, и их величины будут характеризовать вклад каждого фактора в выходной параметр Y. Кроме того, следует отметить, что диагональные элементы ковариационной матрицы будут равны между собой, поэтому все коэффициенты регрессии b_i будут определяться с одинаковой точностью. С учетом сказанного, при обработке результатов активного эксперимента коэффициенты уравнения регрессии по методу наименьших квадратов будут определяться следующим образом:

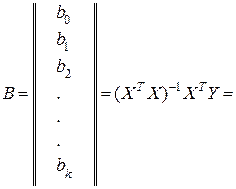
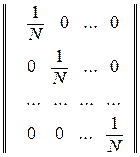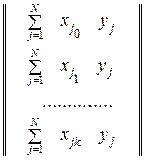. . (3.26)

Из выражения (3.26) следует, что любой коэффициент уравнения регрессии b_i определяется скалярным произведением столбца y на соответствующий столбец x_i деленным на число опытов N в матрице планирования:

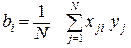. (3.27)

Вычислив вектор В и записав уравнение приближенной регрессии, приступают к его статистическому анализу.

3.3.2 Особенности статистического анализа уравнения регрессии

Так же, как и при обработке результатов пассивного эксперимента, статистический анализ начинают с проверки адекватности уравнения приближенной регрессии результатам эксперимента. Адекватность уравнения проверяется по критерию Фишера:

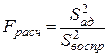. (3.28)

При этом сравниваются между собой дисперсия адекватности 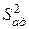и дисперсия воспроизводимости 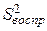. Рассмотрим физический смысл и причины использования в зависимости (3.28) оценок дисперсий 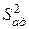и .

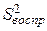Если бы заранее нам было известно, что полученная математическая модель адекватно описывает процесс, то в качестве оценки дисперсии адаптивной помехи (шума эксперимента) 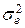можно было бы взять остаточную дисперсию (смотреть 3.23) 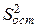. В этом случае, согласно (3.19) для проверки адекватности следовало бы воспользоваться отношением остаточной дисперсии 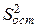к дисперсии воспроизводимости .

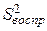То есть для адекватной модели единственной причиной различий между фактическим значением отклика 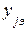и предсказанным по уравнению регрессии 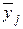может быть влияние шума 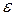. Именно поэтому остаточная дисперсия служит оценкой для 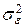. В случае, когда математическая модель неадекватна, остаточная дисперсия 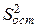будет оценивать одновременно 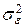и плюс еще некоторую дополнительную компоненту рассеяния, обусловленную неадекватностью модели.

Но так как адекватность модели нам заранее не известна, то оценку дисперсии аддитивной помехи 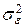на практике определяют по результатам параллельных опытов (повторных наблюдений при одинаковых значениях входных факторов). Эту оценку принято называть дисперсией воспроизводимости .

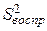Исходя из вышеизложенного, дисперсия адекватности в зависимости (3.28) может быть определена следующим образом:

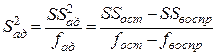, (3.29)

где 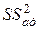– сумма квадратов адекватности;

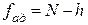– число степеней свободы дисперсии адекватности;

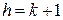– число оценок коэффициентов в уравнении приближенной регрессии (линейный случай);

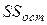– остаточная сумма квадратов;

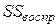– сумма квадратов, связанная с дисперсией воспроизводимости;

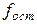– число степеней свободы остаточной дисперсии;

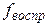– число степеней свободы дисперсии воспроизводимости.

Вид расчётных зависимостей для оценок дисперсий, входящих в (3.28), существенно зависит от порядка проведения активного эксперимента. Следует выделить следующие четыре случая. Случай первый соответствует условиям эксперимента, когда в каждой ячейке матрицы планирования проведено неравное число параллельных опытов, то есть:

.

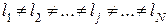Для данного, наиболее общего случая дисперсия адекватности может быть определена по зависимостям:

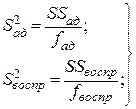, (3.30)

где ;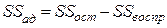

;

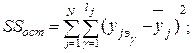
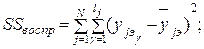
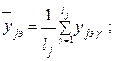
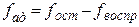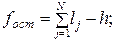
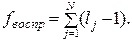
Второй случай соответствует условиям эксперимента, когда в каждой ячейке матрицы планирования проведено равное число параллельных опытов, то есть:

.

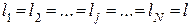Данное условие существенно упрощает расчёты, поэтому, проводя активный эксперимент, исследователь, как правило, стремится к его выполнению. В рассматриваемых условиях оценки дисперсий имеют вид:

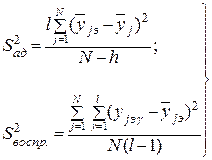. (3.31)

Третий случай соответствует условиям, когда по какой-либо причине параллельные опыты в каждой ячейке матрицы планирования не были проведены. В данных условиях для определения оценок дисперсий целесообразно поставить дополнительную серию из l-го опыта в центре плана эксперимента (когда исследуемые входные факторы находятся на базовых уровнях). В этом случае:

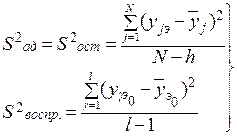, (3.32)

где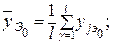

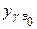значение выходного параметра в γ-м эксперименте для базового уровня входных факторов.

Для учета различных вариантов дублирования опытов при практическом решении задач можно пользоваться таблицей 3.3.

Четвертый случай соответствует условиям, когда параллельные опыты не проводились, и дополнительный эксперимент в центре планов по какой-либо причине поставить не удалось. В этом случае качество аппроксимации опытных данных, полученным уравнением приближенной регрессии, можно оценить, сравнив по критерию Фишера остаточную дисперсию S²_ост. и относительно среднего S²_у, то есть:

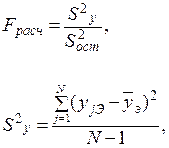(3.33)

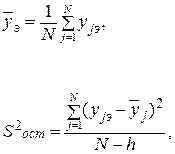
где f₁=N - 1 – число степеней свободы дисперсии относительно среднего S²_y;

f₂=N - h – число степеней свободы остаточной дисперсии.

Таким образом, рассчитав оценки дисперсий воспроизводимости S²_воспр и адекватности S²_ад по зависимости (3.30), (3.31) или (3.32), вычисляют по формуле (3.28) расчетное значение F – критерия и сравнивают его с табличным F_табл. (α, f₁, f₂), определенным для уровня значимости α и чисел степеней свободы f₁ числителя и f₂ знаменателя в формуле (3.28).

Если выполняется условие

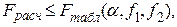
то нет оснований сомневаться в адекватности полученного уравнения приближенной регрессии результатам эксперимента.

Если же:

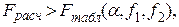
то следует сделать вывод о неадекватности полученной модели и принять меры по ее совершенствованию (например, выбрать полином более высокого порядка или осуществить нелинейное преобразование факторов) с тем, чтобы в конечном итоге получить модель, адекватно отражающую свойства исследуемой системы.

При проверке адекватности уравнения приближенной регрессии по зависимости (3.33) следует помнить, что критериальное отношение показывает, во сколько раз уменьшается рассеяние относительно полученного уравнения регрессии по сравнению с рассеянием относительно среднего. Поэтому, чем больше значение F_расч., полученное по формуле (3.33), будет превышать табличное F_табл. (α, f₁, f₂) определенное для уровня значимости α и чисел степей свободы f₁ – числителя и f₂ – знаменателя в формуле (3.33) тем эффективнее будет уравнение приближенной регрессии.

Получив адекватное уравнение приближенной регрессии, приступают к проверке значимости оценок коэффициентов регрессии. Задача данной проверки, также как и при обработке пассивных экспериментов, заключается в установлении статистической значимости или не значимости отличия оценок коэффициентов регрессии от нуля. В результате этого мы устанавливаем, обусловлено ли отличие b_i от нуля чисто случайным влиянием помехи ε (шума эксперимента) или же это отличие не случайно и вызвано тем, что в истинной регрессионной модели присутствует соответствующий коэффициент регрессии .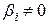

Оценка значимости коэффициентов производится по t – критерию Стьюдента:

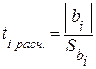, (3.34)

где 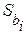– оценка среднего квадратического коэффициента b_i.

Как было отмечено выше, для активного (спланированного) эксперимента все коэффициенты уравнения приближенной регрессии определяются с одинаковой точностью. В случае, когда параллельные опыты отсутствуют, ее можно определить по формуле:

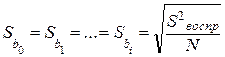. (3.35)

Для различных условий проведения активного эксперимента оценка дисперсии воспроизводимости в формуле (3.35) должна быть рассчитана по зависимостям (3.30), (3.31) или (3.32).

Проверка значимости сводится к последовательной проверке нулевой гипотезы H₀ и конкурирующей гипотезы H₁:

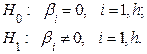
С этой целью расчетное значение t – критерия t_{i расч} для i-й оценки коэффициента регрессии b_i сравнивается с табличным, критическим значением t_табл.(α, f), взятым для уровня значимости α, и числа степеней свободы f=f_воспр. Если выполняется условие:

t_iрасч. > t_табл. (α, f ),

то нулевая гипотеза H₀ принимается. В этом случае коэффициент b_i cчитают статистически не значимым, а его отличие от нуля объясняется лишь действием чисто случайных обстоятельств. Следовательно. Данный коэффициент из уравнения приближенной регрессии может быть исключен при условии, что у исследователя нет никаких дополнительных доводов в пользу его сохранения. Как было сказано выше, при обработке результатов активного (спланированного) эксперимента исключение из уравнения регрессии любого числа незначимых коэффициентов никак не отражается на оставшихся, следовательно, никаких дополнительных перерасчетов делать не следует.

После исключения всех незначимых коэффициентов следует вновь проверить адекватность уравнения приближенной регрессии и, если оно осталось адекватным, можно приступить к его интерпретации.

Примечание. Иногда в процессе исследований встречается случай, когда проверка адекватности полученного уравнения приближенной регрессии становится невозможной. Как правило, это бывает тогда, когда N вариантов варьирования плана полнофакторный эксперимент (ПФЭ) равно числу всех оценок коэффициентов в проверяемом уравнении регрессии. В этом случае знаменатель в зависимостях для расчета дисперсии адекватности обращается в нуль и степеней свободы для проверки гипотезы об адекватности математической модели результатам эксперимента не остается.

В рассматриваемых условиях целесообразно в первую очередь проверить значимость коэффициентов уравнения приближенной регрессии, так как, отбросив незначимые из них, мы получим дополнительные степени свободы для проверки адекватности. Если же все оценки коэффициентов регрессии окажутся значимыми, то есть будут выполняться условия:

N = h;

f_ад = N - h =0,

то в данном случае, очевидно, более корректно будет уменьшить интервалы варьирования входных факторов и вновь провести эксперимент либо сразу перейти к более сложной модели, выбрав полином более высокой степени.