Обработка результатов пассивного эксперимента методом
Регрессионного анализа
Основные понятия классического регрессионного анализа
В пассивном эксперименте исходная информация о функционировании сложной системы может быть получена путем непрерывной или дискретной фиксации уровней исследуемых входных факторов и выходных параметров системы в условиях ее нормального функционирования. В данном случае, как уровни, так и сочетания уровней всех входных факторов в каждый момент времени будут являться случайными величинами. Случайными величинами будут являться и выходные параметры системы. При проведении пассивного эксперимента исследователь каждому сочетанию уровней всех входных факторов должен поставить в соответствие текущий уровень выходных параметров системы. Полученная таким образом информация может быть представлена в виде следующей таблицы.
Таблица 3.1 – Результаты пассивного эксперимента
| Опыты | Входные параметры | Выходные параметры | ||||||||
| x1 | … | xi | … | xk | y1 | … | ys | … | y2 | |
| … j … N | x11 x21 … xj1 … xN1 | … … … … … … | x1i x2i … xji … xNi | … … … … … … | x1k x2k … xjk … xNk | y11 y21 … yj1 … yN1 | … … … … … … | y1s y2s … yjs … yNs | … … … … … … | y1r y2r … yjr … yNr |
Выходные параметры системы ys стохастические связаны с входными факторами xi. В общем виде, эту связь можно представить выражением:
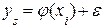 , (3.3)
, (3.3)
где i=1,k;
e –аддитивная помеха, то есть величина, учитывающая случайные ошибки измерений, случайные шумы, влияние неучтенных факторов.
Данную аналитическую зависимость принято называть математической моделью системы, полученной по результатам пассивного эксперимента. Так как математическая модель вида (3.3) находится для каждого выходного параметра системы y1, y2, ..., ys, ..., yr в отдельности, то в дальнейшем будем рассматривать способ ее нахождения лишь в общем виде для одного выходного параметра y.
Выше было отмечено, что истинную зависимость величин X и Y характеризует зависимость условного математического ожидания M[Y/X=x] от параметра. Следовательно, математическую модель (3.3) целесообразно искать в виде уравнения регрессии. Если принять условие, что математическое ожидание аддитивной помехи:
M[e]=0,
то условное математическое ожидание выходного параметра y будет совпадать со значением функции j(xi):
M[Y/Xi=xi]=y=j(xi); (3.4)
где j(xi) – функция регрессии.
Условное математическое ожидание M[Y/Xi=xi], как правило, зависит не только от входных факторов xi, но и от некоторых параметров bi, тогда:
M[Y/Xi=xi]=y=j(xi, bi). (3.5)
В зависимости от того, как данные параметры bi входят в функцию регрессии, модели (3.5) делятся на линейные и нелинейные (по параметрам). Мы будем рассматривать только линейные регрессионные модели.
Точное уравнение регрессии можно получить, только зная M[Y/Xi=xi] для всех допустимых значений переменной xi.
Практически, при проведении экспериментальных исследований такая ситуация невозможна, так как даже отдельные значения M[Y/Xi=xi] не могут быть найдены точно. В связи с этим мы можем искать лишь уравнения приближенной регрессии, оценивая величину и вероятность этой приближенности. Уравнение приближенной регрессии будем записывать в виде:
M[Y/Xi=xi]= 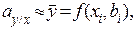 (3.6)
(3.6)
где 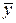 – оценка условного математического ожидания;
– оценка условного математического ожидания;
f(xi,bi) – функция приближенной регрессии;
bi – оценки параметров регрессии.
Вид уравнения приближенной регрессии существенно зависит от выбранного метода приближения. В качестве такого метода в "классическом" регрессионном анализе используется метод наименьших квадратов. Следует отметить, что принцип применения метода наименьших квадратов пригоден для сравнения любого числа функций. Однако при этом удобнее всего сравнивать функции, накладывающие на выборку одинаковое число связей, так как при этом можно сравнивать просто суммы квадратов отклонений. Рассмотрим теоретические основы его применения при обработке результатов пассивного эксперимента.
Так как уровни входных факторов, полученных при испытаниях (смотреть таблицу 3.1), как правило, имеют различный порядок, то для упрощения вычислений все ячейки таблицы 3.1. необходимо отцентрировать и, кроме того, целесообразно добавить первый столбец (x0-фиктивный фактор), состоящий из единиц. Тогда таблица результатов эксперимента приобретет окончательный вид:
Таблица 3.2 - Результаты пассивного эксперимента
| Опыты | Входные параметры | Выходные параметры | ||||||||||
| x0 | 
| … | 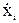
| … | 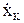
| y1 | … | ys | … | yr | ||
| … j … N | … … | 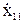
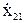 …
…
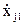 …
…
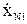
| … … … … … … | 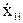
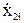 …
…
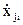 …
…
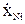
| … … … … … … | 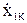
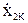 …
…
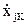 …
…
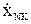
| y11 y21 … yj1 … yN1 | … … … … … … | y1s y2s … yjs … yNs | … … … … … … | y1r y2r … yjr … yNr | |
В данной таблице:
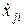 = xji-
= xji- 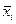 ; (3.7)
; (3.7)
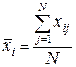 .
.
Очевидно, что ошибка в j-м опыте, которая будет характеризовать точность подбираемой нами математической модели системы, может быть записана в виде:
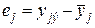 ,
,
где yjэ – величина выходного параметра системы, полученная по результатам эксперимента в j-м опыте;
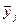 – величина выходного параметра системы, рассчитанная для j-го опыта по подобранной математической модели (3.6).
– величина выходного параметра системы, рассчитанная для j-го опыта по подобранной математической модели (3.6).
Целесообразно так подобрать математическую модель, чтобы по всем опытам выполнялось условие:
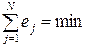 . (3.8)
. (3.8)
Однако, чтобы избежать выполнения данного условия из-за взаимного погашения слагаемых с различными знаками, следует взять условие:
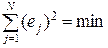 . (3.9)
. (3.9)
Таким образом, мы пришли к методу наименьших квадратов:
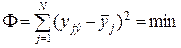 . (3.10)
. (3.10)
Выражение (3.10) минимизирует сумму квадратов остатков или невязок, которые вызываются двумя причинами: отличием оценок bi от истинных параметров bi и наличием аддитивной помехи e.
Если в выражении (3.10) функция Ф есть дифференцируемая функция по всем своим параметрам bi и требуется так подобрать данные параметры, чтобы выполнялось условие минимума, то необходимым условием этого будет являться равенство нулю ее частных производных по всем параметрам bi:
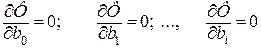 . (3.11)
. (3.11)
Эти равенства можно рассматривать как уравнения относительно неизвестных параметров b0, b1, ..., bi, ..., bk, которые в математической статистике принято называть "системой нормальных уравнений". Так как функция 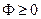 при любых значениях bi, то у нее обязательно существует хотя бы один минимум. Используя правила дифференцирования, системе уравнений (3.11) обычно придают несколько иной вид:
при любых значениях bi, то у нее обязательно существует хотя бы один минимум. Используя правила дифференцирования, системе уравнений (3.11) обычно придают несколько иной вид:
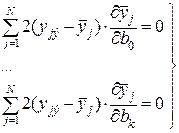 . (3.12)
. (3.12)
Или после дальнейших преобразований:
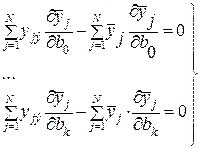 . (3.13)
. (3.13)
Решить систему уравнений (3.13) в общем виде нельзя, для этого следует задаться конкретным видом функции:
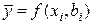 .
.
Так как подбираемая по результатам эксперимента математическая модель системы, как правило, по своему виду не имеет ничего общего с природой процессов, происходящих в системе, то в качестве функции f(xi,bi) целесообразно выбирать простые аналитические зависимости. Таковыми могут быть системы ортогональных полиномов того или иного класса (полиномов Эрмита, Лежандра и другие) тригонометрические функции и т.п. На практике наиболее часто используются полиномы - многочлены различной степени.
Вид многочлена (порядок) можно выбирать, исходя из визуальной оценки характера расположения точек на поле корреляции, опыта предыдущих исследований или исходя из соображений профессионального характера, основанные на знании физической сущности исследуемого процесса. Однако считается, что на начальном этапе исследования более целесообразно ограничиться полиномом первого порядка.
Таким образом, теоретически считается, что в регрессионном анализе вид функции f(xi,bi) известен и требуется по экспериментальным данным с помощью N опытов найти лишь неизвестные параметры bi.
Для решения системы (3.13) выдвигаем гипотезу о наиболее простом (линейном) виде функции f(xi,bi), то есть:
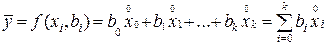 , (3.14)
, (3.14)
где b0, b1,…, bk – вектор независимых коэффициентов (параметров) линейного полинома.
В данном случае частные производные в выражении (3.13) будут равны:
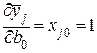 ;
; 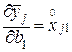 ; … ;
; … ; 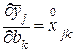 . (3.15)
. (3.15)
Тогда система уравнений (3.13) с учетом (3.15) преобразуется к виду:
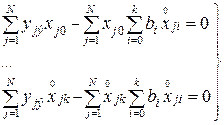 . (3.16)
. (3.16)
Решение системы нормальных уравнений (3.16) целесообразно вести в матричной форме. С этой целью представим ее в следующем виде:
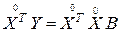 , (3.17)
, (3.17)
где 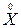 – матрица входных переменных;
– матрица входных переменных;
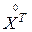 – транспонированная матрица к матрице
– транспонированная матрица к матрице 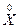 ;
;
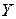 – матрица – столбец выходного параметра;
– матрица – столбец выходного параметра;
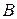 – матрица- столбец коэффициентов регрессии.
– матрица- столбец коэффициентов регрессии.
Для определения коэффициентов регрессии умножим обе части выражения (3.17) на 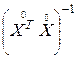 слева, тогда получим:
слева, тогда получим:
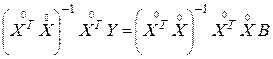 ,
,
откуда:
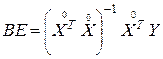 ,
,
где Е – единичная матрица
или
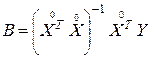 , (3.18)
, (3.18)
где 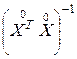 – матрица, обратная матрице
– матрица, обратная матрице 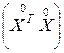 .
.
Следует отметить, что для существования обратной матрицы матрица 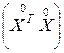 должна быть невырожденной (неособенной). В связи с этим при использовании данного вычислительного метода необходимо, чтобы входные переменные х1, х2, …, хk были линейно независимы. Тогда в матрице независимых входных переменных элементы одного столбца не будут линейной комбинацией соответствующих элементов других столбцов. Если же, по каким-то причинам, матрица
должна быть невырожденной (неособенной). В связи с этим при использовании данного вычислительного метода необходимо, чтобы входные переменные х1, х2, …, хk были линейно независимы. Тогда в матрице независимых входных переменных элементы одного столбца не будут линейной комбинацией соответствующих элементов других столбцов. Если же, по каким-то причинам, матрица 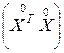 является вырожденной, то следует либо попытаться выразить модель через меньшее число параметров, либо выдвинуть дополнительные ограничения на параметры.
является вырожденной, то следует либо попытаться выразить модель через меньшее число параметров, либо выдвинуть дополнительные ограничения на параметры.
Нахождение обратной матрицы 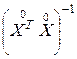 – это задача более сложная, чем просто решение системы линейных алгебраических уравнений, так как ее элементы определяются путем деления алгебраического дополнения элемента
– это задача более сложная, чем просто решение системы линейных алгебраических уравнений, так как ее элементы определяются путем деления алгебраического дополнения элемента 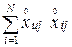 в матрице
в матрице 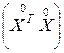 на ее определитель.
на ее определитель.
В качестве примера приведем общие формулы для обращения матриц порядка 2 и 3, которые имеют вид:
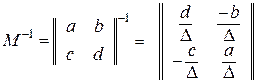 ,
,
где ∆=ad-bc – определитель 2*2 – матрицы М;
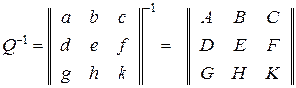 ,
,
где
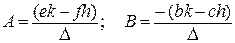 ;
;
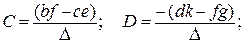
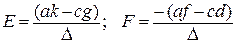 ;
;
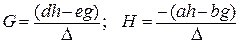 ;
;
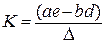 ;
;
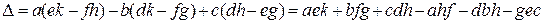 ,
,
где ∆ – определитель матрицы Q.
Матрицы вида 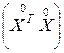 , встречающиеся в регрессионном анализе, всегда симметричны. У этой матрицы элемент j-ой строки и i-го столбца равен элементу i-й строки и j-го столбца, то есть имеет место симметрия элементов квадратной матрицы относительно ее главной диагонали, соединяющей левый верхний элемент с правым нижним. Следовательно, транспонирование симметричной матрицы не меняет ее. Таким образом, если матрица М порядка 2 симметрична, то b = c и обратная матрица будет также симметричной. Если матрица Q , упомянутая выше, симметрична, то b = d, c = g, f = h. Тогда переобозначая матрицу Q в матрицу S, мы получим также симметричную обратную матрицу:
, встречающиеся в регрессионном анализе, всегда симметричны. У этой матрицы элемент j-ой строки и i-го столбца равен элементу i-й строки и j-го столбца, то есть имеет место симметрия элементов квадратной матрицы относительно ее главной диагонали, соединяющей левый верхний элемент с правым нижним. Следовательно, транспонирование симметричной матрицы не меняет ее. Таким образом, если матрица М порядка 2 симметрична, то b = c и обратная матрица будет также симметричной. Если матрица Q , упомянутая выше, симметрична, то b = d, c = g, f = h. Тогда переобозначая матрицу Q в матрицу S, мы получим также симметричную обратную матрицу:
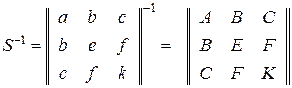 ,
,
где
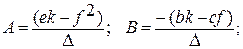
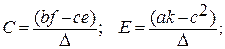
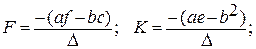
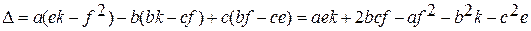 ,
,
где ∆ – определитель матрицы S.
Итак, можно сделать следующий вывод: обратная матрица от любой симметричной матрицы есть симметричная матрица.
Матрицы, имеющие порядок больше трех, обычно трудно обращать, если они не имеют специальной формы. Матрица, которая легко обращается независимо от ее порядка, - это диагональная матрица, которая содержит ненулевые элементы только на главной диагонали, а остальные элементы нули. Обратная матрица от нее получается путем обращения всех ненулевых элементов и сохранения их на тех же позициях, что и в исходной матрице. Например,
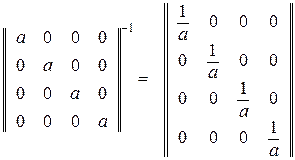 .
.
На этом важном свойстве мы остановимся ниже более подробно.
Таким образом, решение системы нормальных уравнений (3.16) в матричной форме (3.17) имеет вид:
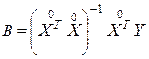 .
.
Каждый коэффициент уравнения регрессии будет определяться по формуле:
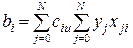 ,
,
где сiu – элементы обратной матрицы 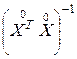 .
.
В результате проведения всех этих операций получим полином первой степени (3.14) с известными коэффициентами bi. Этот полином является аппроксимацией функции (3.5), вид которой исследователю неизвестен.
После расчета коэффициентов bi полученное уравнение приближенной регрессии (3.14) подвергается статистическому анализу.
При этом оценивают ошибку от замены истинной регрессии приближенной и проверяют значимость всех слагаемых найденного уравнения в сравнении со случайной ошибкой наблюдений. Данный комплекс мероприятий носит название «регрессионного анализа».
Особо следует подчеркнуть, что излагаемый порядок проведения «классического» регрессионного анализа возможен только при выполнении следующих предпосылок.
1) Ошибка измерения входных факторов Х равна нулю. Данное категорическое требование, конечно, никогда не может быть выполнено в полной мере. Его следует понимать таким образом, что фактор, вносимый случайными ошибками измерения факторов Х в дисперсию воспроизводимости эксперимента, должен быть пренебрежимо мал по сравнению с действием других неконтролируемых факторов, образующих ошибку эксперимента.
2) Аддитивная помеха (шум эксперимента) e является случайной величиной, распределенной по нормальному закону с математическим ожиданием M[e]=0 и постоянной дисперсией 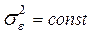 . Значения помехи e в различных наблюдениях являются некоррелированными величинами, то есть
. Значения помехи e в различных наблюдениях являются некоррелированными величинами, то есть 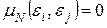 .
.
3) При наличии параллельных опытов оценки дисперсий выходного параметра S12, S22, …, SN2 должны быть однородны. (Однородность оценок дисперсий при одинаковом числе параллельных опытов для каждой серии реализаций проверяют по критерию Кохрена, а при разном – по критерию Бартлетта).
4) Результаты наблюдений над выходной величиной Y представляют собой независимые, нормально распределенные случайные величины. Данное требование не является безусловным, так как метод наименьших квадратов можно применять для определения коэффициентов уравнения регрессии, если даже нет нормального распределения Y, но при этом уже ничего нельзя сказать о его эффективности, особенно при выборках малого объема. Поэтому целесообразно попытаться преобразовать случайную величину Y к нормальному закону.
Дата добавления: 2021-11-16; просмотров: 621;











