Показатели времени решения анаграмм (сек)
| Код имени испытуемого | Анаграмма 1 КРУА (РУКА) | Анаграмма 2 АЛСТЬ (СТАЛЬ) | Анаграмма 3 ИНААМШ (МАШИНА) |
| 1. Л-в | 235* | ||
| 2. П-о | |||
| 3. К-в | |||
| 4. Ю-ч | |||
| 5. Р-о | |||
| Суммы | |||
| Средние | 10,2 | 248,8 | 9,4 |
*Испытуемый Л-в так и не смог правильно решить анаграмму 2.
АЛГОРИТМ
подсчета критерия χr2 Фридмана
1. Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах.
2. Проделать то же самое по отношению ко всем другим испытуемым.
3. Просуммировать ранги по условиям, в которых осуществлялись замеры. Проверить совпадение общей суммы рангов с расчетной суммой.
4. Определить эмпирическое значение χr2 по формуле:
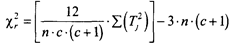
где с – количество условий;
n – количество испытуемых;
Тj – суммы рангов по каждому из условий.
5. Определить уровни статистической значимости для χr2:
а) при с = 3, n ≤ 9 – по таблице 5-А приложения 1;
б) при с = 4, n ≤ 4 – по таблице 5-Б приложения 1.
6. При большем количестве условий и/или испытуемых – определить количество степеней свободы ν по формуле:
ν = c – l,
где с – количество условий (замеров).
По таблице 16 приложения 1 определить критические значения критерия χ2 при данном числе степеней свободы ν. Если эмпирическое значение χr2 равно критическому значению χr2 или превышает его, различия достоверны.
Проранжируем значения, полученные по трем анаграммам каждым испытуемым. Например, испытуемый К-в меньше всего времени провел над анаграммой 1 – следовательно, она получает ранг 1. На втором месте у него стоит анаграмма 3 – она получает ранг 2. Наконец, анаграмма 2 получает ранг 3, потому что она решалась им дольше двух других.
Сумма рангов по каждому испытуемому должна составлять 6. Расчетная общая сумма рангов в критерии определяется по формуле:
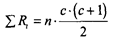
где n – количество испытуемых;
с – количество условий измерения (замеров).
В данном случае,
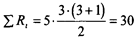
Таблица 12.7
Показатели времени решения анаграмм 1, 2, 3 и их ранги (n = 5)
| Код имени испытуемого | Анаграмма 1 | Анаграмма 2 | Анаграмма 3 | |||
| Время (сек) | Ранг | Время (сек) | Ранг | Время (сек) | Ранг | |
| 1. Л-в | ||||||
| 2. П-о | ||||||
| 3. К-в | ||||||
| 4. Ю-ч | ||||||
| 5. Р-о | ||||||
| Суммы |
Общая сумма рангов составляет: 6 + 15 + 9 = 30, что совпадает с расчетной величиной.
Мы помним, что испытуемый Л-в провел 3 минуты и 55 сек над решением второй анаграммы, но так и не решил ее. Поскольку он решал ее дольше остальных двух анаграмм, мы имеем право присвоить ей ранг 3. Ведь назначение трех первых анаграмм – подготовить испытуемого к тому, что над следующей анаграммой ему, возможно, придется думать еще дольше, в то время как сам факт нахождения правильного ответа не так существен.
Сформулируем гипотезы.
H0: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, являются случайными.
H2: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, не являются случайными.
Теперь нам нужно определить эмпирическое значение χr2 по формуле:
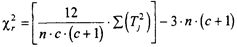 ,
,
где с – количество условий;
n – количество испытуемых;
Tj – суммы рангов по каждому из условий.
Определим χr2 для данного случая:
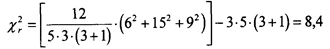
Поскольку в данном примере рассматриваются три задачи, то есть 3 условия, с = 3. Количество испытуемых n = 5. Это позволяет нам воспользоваться специальной таблицей χr2, а именно таблицей 5-A приложения 1. Эмпирическое значение χr2 при с = 3, n = 5 точно соответствует уровню значимости р=0,0085.
Ответ: H0 отклоняется. Принимается H1. Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, неслучайны (р = 0,0085).
Дата добавления: 2021-11-16; просмотров: 578;











