Сравнение эмпирического распределения с теоретическим
В разных задачах подсчет теоретических частот осуществляется по-разному. Рассмотрим примеры задач, иллюстрирующих различные варианты подсчета теоретических частот. Начнем с равновероятного распределения теоретических частот. В задачах такого типа (13.1, 13.2 и 13.3) в силу требования равномерности распределения все теоретические частоты должны быть равны между собой.
Пример 13.1. Предположим, что в эксперименте психологу необходимо использовать шестигранный игральный кубик с цифрами на гранях от 1 до 6. Для чистоты эксперимента необходимо получить «идеальный» кубик, т. е. такой, чтобы при достаточно большом числе подбрасываний, каждая его грань выпадала бы примерно равное число раз. Задача состоит в выяснении того, будет ли данный кубик близок к идеальному?
Решение. Для решения этой задачи, психолог подбрасывал кубик 60 раз, при этом количество выпадений каждой грани (эмпирические частоты fэ) распределилось следующим образом:
Таблица 13.1
| Грани кубика | ||||||
| Fэ – эмпирические частоты | ||||||
| fm – теоретические частоты |
Сформулируем гипотезы
Н0: Эмпирическое и теоретическое распределения не различаются между собой.
Н1: Эмпирическое и теоретическое распределения различаются между собой.
В «идеальном» случае необходимо, чтобы каждая из 6 его граней (теоретические частоты) выпадала бы равное число раз: 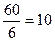 . Величина
. Величина 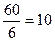 и будет, очевидно, теоретической частотой (fm), одинаковой для каждой грани кубика.
и будет, очевидно, теоретической частотой (fm), одинаковой для каждой грани кубика.
Согласно данным таблицы 13.1 легко подсчитать величину χ2эмп (хи-квадрат эмпирическое) по формуле (13.1).
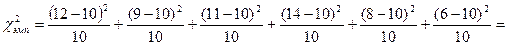
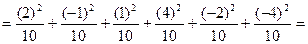
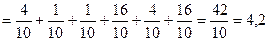 .
.
Теперь, для того чтобы найти χ2кр, необходимо обратиться к Таблице 16 приложения 1, определив предварительно число степеней свободы ν. В нашем случае к (число граней) = 6, следовательно, ν = 6 – 1 = 5. По таблице 16 приложения 1 находим величины χ2кр для уровней значимости 0,05 и 0,01:
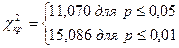
Строим «ось значимости».

В нашем случае χ2эмп попало в зону незначимости и оказалось равным 4,2, что гораздо меньше 11,070 – критической величины для 5% уровня значимости. Следовательно, можно принимать гипотезу Н0 о том, что эмпирическое и теоретическое распределения не различаются между собой. Таким образом, можно утверждать, что игральный кубик «безупречен».
Понятно также, что если бы χ2эмп попало в зону значимости, то следовало бы принять гипотезу Н1 о наличии различий и тем самым утверждать, что наш игральный кубик был бы далеко не «безупречен».
Пример 13.2. В эксперименте испытуемый должен произвести выбор левого или правого стола с заданиями. В инструкции психолог подчеркивает, что задания на обоих столах одинаковы. Из 150 испытуемых правый стол выбрали 98 человек, а левый 52. Можно ли утверждать, что подобный выбор левого или правого стола равновероятен или он обусловлен какой-либо причиной, неизвестной психологу?
Решение. Подчеркнем, что данная задача вновь на сопоставление экспериментального распределения с теоретическим. Каковы в этом случае параметры теоретического распределения? Предполагается, что выбор должен быть равновероятным, т. е. правый и левый стол должны выбрать одинаковое количество испытуемых, а это 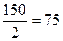 человек.
человек.
Проверим совпадение эмпирического распределения с теоретическим по критерию хи-квадрат. Лучше всего для расчета критерия использовать таблицу 13.2, последовательность вычислений в которой соответствует формуле (13.1).
Таблица 13.2
| № 1 | № 2 | № 3 | №4 | №5 | № 6 |
| Альтернативы выбора стола | fэ | fm | 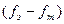
| 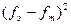
| 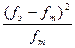
|
| 1 (правый) | 7,05 | ||||
| 2 (левый) | -23 | 7,05 | |||
| Суммы | χ2эмп=14,1 |
Сформулируем гипотезы
Н0: Правый и левый стол выбирают одинаковое количество испытуемых.
Н1: Правый и левый стол выбирают не одинаковое количество испытуемых.
В таблице 13.2 альтернатива 1 соответствует выбору правого стола, а альтернатива 2 – выбору левого. Второй и третий столбцы таблицы, соответственно, эмпирические и теоретические частоты. Следует просуммировать эти два столбца, чтобы проверить равенство сумм эмпирических и теоретических частот. Четвертый столбец соответствует разности между эмпирическими и теоретическими частотами (fэ – fт). В нижней строчке столбца эти разности просуммированы. Полученная сумма равна 0. В дальнейших расчетах величина этой суммы не используется, но ее обязательно следует каждый раз вычислять, поскольку ее равенство нулю гарантирует правильность вычислений на этом этапе. Если же сумма элементов четвертого столбца не равна нулю, это означает, что в расчеты вкралась ошибка.
В нашем случае эмпирическая величина хи-квадрат, вычисленная по формуле (13.1), равна 14,1 и является суммой чисел в шестом столбце. Для того чтобы найти табличные значения χ2кр, следует определить число степеней свободы по формуле: ν = k – 1, где k – количество альтернатив (строк). В нашем случае k = 2, следовательно, ν = 2 – 1 = 1. По таблице 16 приложения 1 находим:
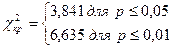
Строим «ось значимости».

Полученные различия оказались значимыми на уровне 1%. Иными словами, испытуемые статистически значимо предпочитают выбор правого стола. В терминах статистических гипотез этот вывод звучит так: выбор направления оказался не случайным, поэтому нулевая гипотеза Н0 о сходстве отклоняется и на высоком уровне значимости принимается альтернативная гипотеза Н1 о различии. Если психологу интересны причины подобного выбора, то их следует выяснять в специальном эксперименте.
Пример 13.3. Психолог решает задачу: будет ли удовлетворенность работой на данном предприятии распределена равномерно по следующим альтернативам (градациям):
1 – работой вполне доволен;
2 – скорее доволен, чем не доволен;
3 – трудно сказать, не знаю, безразлично;
4 – скорее недоволен, чем доволен;
5 – совершенно недоволен работой.
Решение. Для решения этой задачи производится опрос случайной выборки из 65 респондентов (испытуемых) об удовлетворенности работой: «В какой степени Вас устраивает Ваша теперешняя работа?», причем ответы должны даваться согласно вышеозначенным альтернативам.
Полученные ответы (эмпирические частоты) представлены в таблице 13.3 в столбце № 2. В этой же таблице в третьем столбце даны теоретические частоты для данной выборки испытуемых, которые, согласно предположению психолога, должны быть одинаковы и равняться: 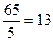 . В следующих столбцах таблицы 13.3 приведены необходимые расчеты по формуле (13.1).
. В следующих столбцах таблицы 13.3 приведены необходимые расчеты по формуле (13.1).
Таблица 13.3
| № 1 | № 2 | №3 | №4 | №5 | №6 |
| Альтернативы | fэ | fm | 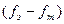
| 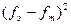
| 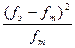
|
| -5 | 1,92 | ||||
| +9 | 6,23 | ||||
| + 1 | 0,08 | ||||
| -4 | 1,23 | ||||
| -1 | 0,08 | ||||
| Суммы | χ2эмп = 9,54 |
Сформулируем гипотезы
Н0: Удовлетворенность работой на данном предприятии распределена равномерно по перечисленным альтернативам.
Н1: Удовлетворенность работой на данном предприятии распределена не равномерно по перечисленным альтернативам.
Напомним, что сумма величин (fэ – fm) в столбце № 4 должна равняться нулю. Это показатель правильности вычислений.
В шестом столбце таблицы подсчитана величина χ2эмп, равная 9,54. Для того чтобы найти табличные значения χ2кр для двух уровней значимости, следует вначале определить число степеней свободы по формуле: ν = k – 1, где k – количество альтернатив (строк). В нашем случае k = 5, следовательно, ν = 5 – 1 = 4. По таблице 16 приложения 1 находим:
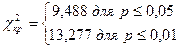
Строим «ось значимости».
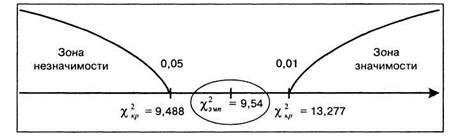
Величина χ2эмп попала в зону неопределенности. Можно считать, однако, что полученные различия значимы на уровне 5% и принять гипотезу Н1 о различии теоретического и эмпирического распределений. Психолог может предположить, что на 5% уровне значимости выбор альтернатив респондентами не равновероятен. Таким образом, можно сказать, что эмпирическое распределение выбора альтернатив значимо отличается от теоретически предположенного равномерного выбора альтернатив. Причину этого, а также степень отвержения или предпочтения работы на данном предприятии психолог может выяснить в специальном исследовании.
При решении приведенных выше трех задач с равновероятным распределением теоретических частот не было необходимости использовать специальные процедуры их подсчета. Однако на практике чаще возникают задачи, в которых распределение теоретических частот не имеет равновероятного характера. В этих случаях для подсчета теоретических частот используются специальные формулы или таблицы. Рассмотрим задачу, в которой в качестве теоретического будет использоваться нормальное распределение
Пример 13.4. У 267 человек был измерен рост. Вопрос состоит в том, будет ли полученное в этой выборке распределение роста близко к нормальному? (Задача взята из учебника Лакина Г. Ф. Биометрия, 1990).
Решение. Измерения проводились с точностью до 0,1 см и все полученные величины роста оказались в диапазоне от 156,5 до 183,5 см. Для расчета по критерию хи-квадрат целесообразно разбить этот диапазон на интервалы, величину интервала удобнее всего взять равной 3 см, поскольку 183,5 – 156,5 = 27 и 27 делится нацело на 3 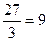 . Таким образом, все экспериментальные данные будут распределены по 9 интервалам. При этом центрами интервалов будут следующие числа: 158 (поскольку 156,5 + 159,5 = 316 и
. Таким образом, все экспериментальные данные будут распределены по 9 интервалам. При этом центрами интервалов будут следующие числа: 158 (поскольку 156,5 + 159,5 = 316 и 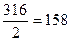 ), 161 (поскольку 159,5 + 162,5 = 322 и
), 161 (поскольку 159,5 + 162,5 = 322 и 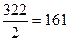 ), 164 и т. д. до 182.
), 164 и т. д. до 182.
При измерении роста в каждый из этих интервалов попало какое-то количество людей – эта величина для каждого интервала и будет эмпирической частотой, обозначаемой в дальнейшем как fэj.
Расчетная формула критерия хи-квадрат для сравнения двух эмпирических распределений в зависимости от вида представленных данных может иметь следующий вид:
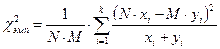 , (13.2)
, (13.2)
где N и М – соответственно число элементов а первой и во второй выборке. Эти числа могут совпадать, а могут быть и различными.
Сформулируем гипотезы
Н0: Полученное в этой выборке распределение роста близко к нормальному.
Н1: Полученное в этой выборке распределение роста отличается от нормального.
Чтобы применить расчетную формулу (13.1), необходимо прежде всего вычислить теоретические частоты. Для этого по всем полученным значениям эмпирических частот (по всем выборочным данным) нужно вычислить:
1) среднее Mx;
2) и среднеквадратическое отклонение (σ).
Для наших выборочных данных величина среднего Mх оказалась равной 166,22 и среднеквадратическое σ = 4,06.
Затем для каждого выделенного интервала следует подсчитать величины oi по формуле (13.3) (где индекс i изменяется от 1 до 9, т. к. у нас 9 интервалов):
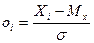 . (13.3)
. (13.3)
Величины oi называются нормированными частотами. Удобнее производить их расчет в приведенной ниже таблице 13.4. Подсчитав эти величины, необходимо занести их в соответствующую строчку третьего столбца таблицы 13.4.
Затем по величинам нормированных частот по таблице 15 приложения 1 находятся величины f(oi), которые называются ординатами нормальной кривой для каждой oi. Величины f(oi), полученные из таблицы 15 приложения 1, заносятся в соответствующую строчку четвертого столбца таблицы 13.4. Величины, полученные в третьем и четвертом столбцах таблицы 13.4, позволяют вычислить по соответствующей формуле необходимые нам теоретические частоты (обозначаемые как fmi) и также занести их в пятый столбец таблицы 13.4.
Расчет теоретических частот осуществляется для каждого интервала по следующей формуле
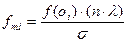 , (13.4)
, (13.4)
где n = 267 (общая величина выборки),
λ = 3 (величина интервала) и
σ – среднеквадратичное отклонение.
Напомним, что после подсчета эти величины заносятся в соответствующую строчку пятого столбца таблицы 13.4.
Таблица 13.4
| № 1 | №2 | №3 | №4 | № 5 |
| Центры интервалов xi | Эмпирические частоты fэi | 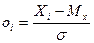
| Ординаты нормальной кривой f(oi) | Расчетные теоретические частоты fmi |
| -2,77 | 0,0086 | 1,6 | ||
| -2,03 | 0,0508 | 10,0 | ||
| -1,29 | 0,1736 | 34,3 | ||
| -0,55 | 0,3429 | 67,8 | ||
| +0,19 | 0,3918 | 77,6 | ||
| +0,93 | 0,2589 | 51,2 | ||
| + 1,67 | 0,0989 | 19,5 | ||
| +2,41 | 0,0219 | 4,4 | ||
| +3,15 | 0,0028 | 0,6 | ||
| Суммы | — | — | 267,0 |
Рассмотрим более детально, как получаются необходимые нам показатели на примере первой строчки таблицы 13.4.
Так, согласно экспериментальным данным в первый интервал, т. е. в интервал от 156,5 см до 159,5 см, попало 3 человека (или соответствующая эмпирическая частота fэi = 3). Мы помним, что величина средней Mx для данной выборки равна 169,22 см, а величина σ = 4,06.
Проведем расчет величины ol для первого интервала по формуле (13.3):
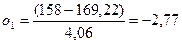 .
.
Подставляем полученную величину в первую строчку третьего столбца таблицы 13.4. Дальнейший расчет производится с модулями этих чисел.
Величину f(oi) = 0,0086 находим в таблице 15 приложения 1 на пересечении строчки с числом 2,7 (десятые доли) и столбца с числом 7 (сотые доли). Заносим эту величину в первую строчку четвертого столбца таблицы 13.4.
Теоретическую частоту fmi получаем в соответствии с формулой (13.4):
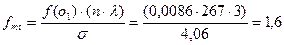 .
.
Заносим полученное число в первую строчку пятого столбца таблицы 13.4. Подобная процедура повторяется далее для каждого интервала.
Теперь у нас все готово для работы с критерием хи-квадрат по формуле 13.1 на основе стандартной таблицы. В целях упрощения расчетов сократим число интервалов до 7. Это делается следующим образом: складываем две верхние частоты и две нижние, то есть: 3 + 9 = 12 и 1 + 5 = 6. Тогда стандартная таблица для вычисления хи-квадрат выглядит следующим образом.
Таблица 13.5
| № 1 | №2 | №3 | №4 | №5 | №6 |
| Альтернативы | fэ | fm | 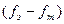
| 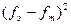
| 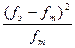
|
| 11,6 | +0,4 | 0,16 | 0,01 | ||
| 34,3 | –3,3 | 10,89 | 0,32 | ||
| 67,8 | + 3,2 | 10,24 | 0,15 | ||
| 77,6 | + 4,4 | 19,36 | 0,25 | ||
| 51,2 | –5,2 | 27,04 | 0,53 | ||
| 19,5 | –0,5 | 0,25 | 0,01 | ||
| 5,0 | + 1,0 | 1,00 | 0,20 | ||
| Суммы | χ2эмп=1,47 |
В случае оценки равенства эмпирического распределения нормальное число степеней свободы определяется особым образом: из общего числа интервалов вычитают число 3. В данном случае: 7 – 3 = 4. Таким образом, число степеней свободы v в нашем случае будет равно ν = 4. По таблице 16 приложения 1 находим:
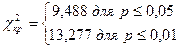
Строим «ось значимости».
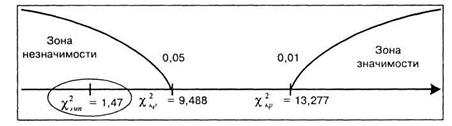
Полученная величина эмпирического значения хи-квадрат попала в зону незначимости, поэтому необходимо принять гипотезу Н0 об отсутствии различий. Следовательно, существуют все основания утверждать, что наше эмпирическое распределение близко к нормальному.
В заключение подчеркнем, что, несмотря на некоторую «громоздкость» вычислительных процедур, этот способ расчета дает наиболее точную оценку совпадения эмпирического и нормального распределений.
Дата добавления: 2021-11-16; просмотров: 1263;











