Расчет критерия Т при сопоставлении замеров физического волевого усилия
| Код имени испытуемого | Длительность удержания усилия на динамометре (с) | Разность (tпосле -tдо) | Абсолютное значение разности | Ранговый номер разности | ||
| До измерения волевых качеств и обращения к идеалу (tдо) | После измерения волевых качеств и обращения к идеалу (tпосле) | |||||
| Г. | -39 | |||||
| Кос | -27 | |||||
| 3* | Крив. | +3 | ||||
| Кур. | -19 | |||||
| Л | -38 | 9,5 | ||||
| М | -8 | |||||
| 7* | Р. | +4 | 2,5 | |||
| С. | -4 | 2.5 | ||||
| Т. | -38 | 9.5 | ||||
| 10* | Х. | +25 | ||||
| Ю. | -18 | |||||
| Сумма |
АЛГОРИТМ
подсчета критерия Т Вилкоксона
1. Составить список испытуемых в любом порядке, например, алфавитном.
2. Вычислить разность между индивидуальными значениями во втором и первом замерах («после» – «до»). Определить, что будет считаться «типичным» сдвигом и сформулировать соответствующие гипотезы.
3. Перевести разности в абсолютные величины и записать их отдельным столбцом (иначе трудно отвлечься от знака разности).
4. Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.
5. Отметить кружками или другими знаками ранги, соответствующие сдвигам в «нетипичном» направлении.
6. Подсчитать сумму этих рангов по формуле:
T = ∑Rr.,
где Rr – ранговые значения сдвигов с более редким знаком.
7. Определить критические значения Т для данного n по таблице 12 приложения 1. Если Тэмп меньше или равен Ткр, сдвиг в «типичную» сторону по интенсивности достоверно преобладает.
Для подсчета этого критерия нет необходимости упорядочивать ряды значений по нарастанию признака. Мы можем использовать алфавитный список испытуемых, как в данном случае.
Первый шаг в подсчете критерия Т – вычитание каждого индивидуального значения «до» из значения «после» (можно вычитать значения «после» из значений «до», это никак не повлияет на расчет критерия. Но лучше во всех случаях придерживаться одной системы, чтобы не запутаться самим). Мы видим из таблицы 12.5, что 8 полученных разностей – отрицательные и лишь 3 – положительные. Это означает, что у 8 испытуемых длительность удержания мышечного усилия во втором замере уменьшилась, а у 3 – увеличилась. Мы столкнулись с тем случаем, когда уже сейчас мы не можем сформулировать статистическую гипотезу, соответствующую первоначальному предположению исследователя. Предполагалось, что обращение к идеалу будет увеличивать длительность мышечного усилия, а экспериментальные данные свидетельствуют, что лишь в 3 случаях из 11 этот показатель действительно увеличился. Мы можем сформулировать лишь гипотезу, предполагающую несущественность сдвига этого показателя в сторону снижения.
Сформулируем гипотезы
Н0: Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия не превышает интенсивности сдвигов в сторону ее увеличения.
Н1: Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия превышает интенсивность сдвигов в сторону ее увеличения.
На следующем шаге все сдвиги, независимо от их знака, должны быть проранжированы по выраженности. В таблице 12.5 в четвертом слева столбце приведены абсолютные величины сдвигов, а в последнем столбце (справа) – ранги этих абсолютных величин. Меньшему значению соответствует меньший ранг. При этом сумма рангов равна 66, что соответствует расчетной:
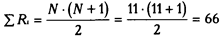
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае – положительными. В таблице 12.5 эти сдвиги и соответствующие им ранги выделены цветом. Сумма рангов этих «редких» сдвигов и составляет эмпирическое значение критерия Т:
T = ∑Rr.,
где Rr – ранговые значения сдвигов с более редким знаком.
Итак, в данном случае, Tэмп = 1 + 2,5 + 7 = 10,5.
По таблице 12 приложения 1 определяем критические значения Т для n = 11:
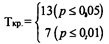 .
.
Построим «ось значимости».
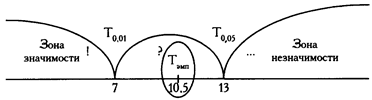
Зона значимости в данном случае простирается влево. Действительно, если бы «редких», в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю. В данном же случае эмпирическое значение Т попадает в зону неопределенности: Тэмп < Tкр (0,05).
Ответ: H0 отвергается. Интенсивность отрицательного сдвига показателя физического волевого усилия превышает интенсивность положительного сдвига (р < 0,05).
Таким образом, исследователю придется признать, что продолжительность удержания мышечного волевого усилия во втором замере снижается, и этот сдвиг неслучаен. Инструкция, ориентирующая испытуемого на соответствие идеалу в развитии воли, оказалась гораздо менее мощным фактором, чем какая-то иная сила – возможно, мышечное утомление, может быть, разочарование в себе или в возможностях данного психологического эксперимента. А может быть, в момент второго замера просто перестает действовать какой-то мощный фактор, который был активен вначале? На все эти вопросы статистические методы не могут ответить, если в схему эксперимента не включена контрольная группа – в данном случае, выборка, уравновешенная с экспериментальной группой по всем значимым характеристикам (полу, возрасту, профессии, месту обучения), у которой просто измерили бы вторично волевое усилие через такой же промежуток времени, не призывая соответствовать идеалу в развитии воли.
12.4. Критерий χr2 Фридмана
Критерий χr 2 применяется для сопоставления показателей, измеренных в трех или более условиях на одной и той же выборке испытуемых.
Критерий позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений.
Данный критерий является распространением критерия Т Вилкоксона на большее, чем 2, количество условий измерения. Однако здесь мы ранжируем не абсолютные величины сдвигов, а сами индивидуальные значения, полученные данным испытуемым в 1, 2, 3 и т. д. замерах.
Например, если у испытуемого в первом замере определена скорость прохождения графического лабиринта 54 сек, во втором замере – 42 сек, а в третьем замере – 63 сек, то эти показатели получат ранги, соответственно, 2, 1, 3, поскольку меньшему значению, полученному во втором замере, мы начислим ранг 1, среднему значению, полученному в первом замере – ранг 2, а наибольшему значению, полученному в третьем замере – ранг 3.
После того, как все значения будут проранжированы, подсчитываются суммы рангов по столбцам для каждого из произведенных замеров.
Если различия между значениями признака, полученными в разных условиях, случайны, то суммы рангов по разным условиям будут приблизительно равны. Но если значения признака изменяются в разных условиях каким-то закономерным образом, то в одних условиях будут преобладать высокие ранги, а в других – низкие. Суммы рангов будут достоверно различаться между собой. Эмпирическое значение критерия χ2r и указывает на то, насколько различаются суммы рангов. Чем больше эмпирическое значение χ2r, тем более существенные расхождения сумм рангов оно отражает.
Если χr2 равняется критическому значению или превышает его, различия статистически достоверны.
Гипотезы
H0: Между показателями, полученными (измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в разных условиях, существуют неслучайные различия.
Ограничения критерия
1. Нижний порог не менее 2-х испытуемых (n≥2), каждый из которых прошел не менее 3-х замеров (с≥3).
2. При с = 3, n ≤ 9, уровень значимости полученного эмпирического значения χr2 определяется по таблице 5-A приложения 1; при с = 4, n ≤ 4, уровень значимости полученного эмпирического значения χr2 определяется по таблице 5-Б приложения 1; при больших количествах испытуемых или условий полученные эмпирические значения χr2 сопоставляются с критическими значениями χ2, определяемыми по таблице 16 приложения 1. Это объясняется тем, что χr2 имеет распределение, сходное с распределением χ2. Число степеней свободы ν определяется по формуле
ν = c – l,
где с – количество условий измерения (замеров).
Пример.В эксперименте по исследованию интеллектуальной настойчивости испытуемым предлагались анаграммы (Сидоренко Е. В., 1984). Анаграммы нужно было подобрать таким образом, чтобы постепенно подготовить испытуемого к самой трудной – а фактически неразрешимой – задаче. Иными словами, испытуемый должен был постепенно привыкнуть к тому, что задачи становятся все более и более трудными и что над каждой последующей анаграммой ему приходится проводить больше времени. Достоверны ли различия во времени решения испытуемыми анаграмм?
Таблица 12.6
Дата добавления: 2021-11-16; просмотров: 654;











