Коэффициент корреляции рангов Спирмена
Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Правила ранжирования варьирующих величин были описаны ранее.
Величина коэффициента линейной корреляции Спирмена также лежит в интервале +1 и -1. Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале.
В принципе число ранжируемых признаков (качеств, черт и т. п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков – затруднителен. Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (n < 40). В случае использования большего, чем 40 числа ранжируемых признаков, уровень значимости коэффициента корреляции следует находить по таблице для коэффициента корреляции Пирсона.
Ранговый коэффициент линейной корреляции Спирмена подсчитывается по формуле:
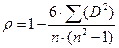 , (9.5)
, (9.5)
где n – количество ранжируемых признаков (показателей, испытуемых);
D – разность между рангами по двум переменным для каждого испытуемого;
∑(D2) – сумма квадратов разностей рангов.
Используя ранговый коэффициент корреляции, решим следующую задачу.
Пример 9.2.Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников, и их средняя успеваемость в конце учебного года.
Решение. Прежде всего, сформулируем гипотезы.
Н0: связь между показателями школьной готовности и итоговыми оценками первоклассников отсутствует.
Н1: связь между показателями школьной готовности и итоговыми оценками первоклассников присутствует.
Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. Результаты представим в таблице 9.2.
Таблица 9.2
| № учащихся п/п | |||||||||||
| Ранги показателей школьной готовности | |||||||||||
| Ранги среднегодовой успеваемости | |||||||||||
| D | -2 | -2 | -2 | -2 | -2 | ||||||
| D2 |
Подставляем полученные данные в формулу (9.5) и производим расчет. Получаем:
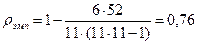 .
.
Для нахождения уровня значимости обращаемся к таблице, в которой приведены критические значения для коэффициентов ранговой корреляции (таблица 2 приложения 1.). Подчеркнем, что в этой таблице, как и в таблице для линейной корреляции Пирсона, все величины коэффициентов корреляции даны по абсолютной величине. Поэтому еще раз напомним, что знак коэффициента корреляции учитывается только при его интерпретации.
Однако, в отличие от таблицы критических значений пирсоновской корреляции, в таблице нахождение уровней значимости осуществляется по числу n, т. е. по числу испытуемых. В нашем случае n = 11. Для этого числа находим ρкр = 0,61 для 0,05 ρкр = 0,76 для 0,01. В стандартной форме записи это выглядит следующим образом:



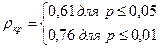
Строим соответствующую «ось значимости».
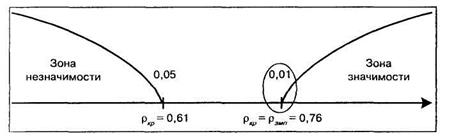
Полученный коэффициент корреляции совпал с критическим значением для уровня значимости в 1%. Следовательно, можно утверждать, что показатели школьной готовности и итоговые оценки первоклассников связаны положительной корреляционной зависимостью – иначе говоря, чем выше показатель школьной готовности, тем лучше учится первоклассник. В терминах статистических гипотез психолог должен отклонить нулевую (Н0) гипотезу о сходстве и принять альтернативную (Н1) о наличии различий, которая говорит о том, что связь между показателями школьной готовности и средней успеваемостью отлична от нуля.
Решим еще одну задачу с использованием коэффициента корреляции Спирмена. Эта задача взята из книги «Психологические исследования. Практикум по общей психологии для студентов педагогических вузов» [34]. В книге эта задача рассматривается как тест на самооценку.
Пример 9.3.Определить связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном».
Решение. Прежде всего, сформулируем гипотезы.
Н0: связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном», отсутствует.
Н1: связь между ранговыми оценками качеств личности, входящими в представление человека о своем «Я реальном» и «Я идеальном», присутствует.
При решении этой задачи мы взяли только 7 качеств, в то время как в психологических практикумах предлагается ранжировать 20 качеств. Решение подобных задач лучше всего оформлять сразу в виде таблицы. В первом столбце таблицы проранжированы 7 качеств личности по отношению к «Я реальному», в третьем столбце таблицы – по отношению к «Я идеальному». В четвертом столбце таблицы представлены величины разности рангов между «Я реальным» и «Я идеальным» со знаками. В последнем столбце таблицы 9.3 эти величины возведены в квадрат.
Таблица 9.3
| № 1 | № 2 | № 3 | № 4 | № 5 |
| Я реальное | Качества личности | Я идеальное | Di | D2i |
| ответственность | ||||
| общительность | -4 | |||
| настойчивость | -4 | |||
| энергичность | -4 | |||
| жизнерадостность | ||||
| терпеливость | ||||
| решительность | ||||
| Сумма |
Сумма Di должна быть равна нулю. Это показатель правильности подсчета разностей.
Производим подсчет коэффициента корреляции по формуле (9.5):
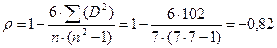 .
.
Обращаемся к таблице для критических значений коэффициентов ранговой корреляции (таблица 2 приложения 1). Для n = 7 находим rкр = 0,78 для Р < 0,05 и 0,94 для Р < 0,01. Представим это в стандартной форме записи:



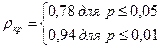
Строим соответствующую «ось значимости».
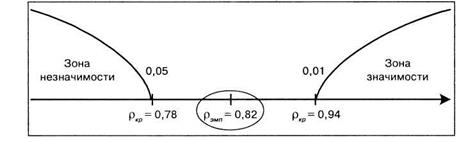
Полученная величина рангового коэффициента корреляции Спирмена попала в зону неопределенности. В данном случае, при столь малом числе анализируемых качеств, на 5% уровне значимости следует принять гипотезу Н1, и отклонить гипотезу Но о сходстве. Учитывая знак коэффициента корреляции – отрицательный, можно утверждать, что у испытуемого достаточно низкая самооценка, поскольку большей величине «Я реального» соответствует меньшая величина «Я идеального».
Дата добавления: 2021-11-16; просмотров: 676;











