Законы распределения отдельных случайных величин, входящих в систему.

Пусть имеется система случайных величин (X, Y), причем известна ее функция распределения F(X, Y) или плотность распределения f(x, y). Требуется найти законы распределения случайных величин X, Y, входящих в систему, т.е. определить выражения для функций .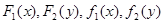

Согласно второму свойству функции распределения случайных величин X, Y равны 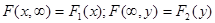. Поэтому для получения функции распределения одной случайной величины, входящей в систему необходимо в функцию распределения системы вместо другой случайной величины подставить « 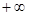». Для отыскания выражения плотности распределения, например, случайной величины X воспользуемся определением ее, т.е.

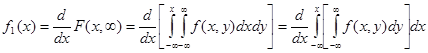, или окончательно

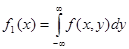. По аналогии .

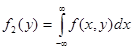Следовательно, для получения плотности распределения одной случайной величины, входящей в систему, необходимо плотность распределения системы f(x, y) проинтегрировать в бесконечных пределах по другой случайной величине как переменной.

Пример 1.Дана система случайных величин (X, Y) с плотностью распределения 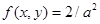для всех точек внутри треугольника (рис. 3.7а), вне треугольника f(x, y)=0. Требуется определить .

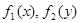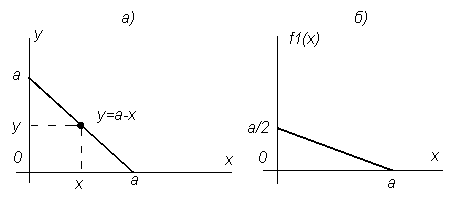
Рисунок 3.7 Иллюстрация к примеру

Решение.

Используя полученное выражение для плотности распределения случайной величины X, получим 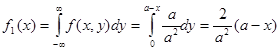. Аналогично находим выражение для плотности распределения случайной величины Y 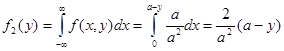(см. рис. 3.7б).