Экспоненциальный закон распределения.
В различных приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике и т.д. широко применяется экспоненциальное (показательное) распределение.
Время занятости канала связи, время безотказной работы ЭВМ, продолжительность поиска чего–либо – все это экспоненциально распределенные случайные величины.
Неотрицательная величина X называется распределенной по экспоненциальному закону, если ее плотность распределения имеет вид
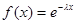 ,
,
где 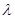 - параметр экспоненциального распределения.
- параметр экспоненциального распределения.
График плотности распределения изображен на рис. 13.
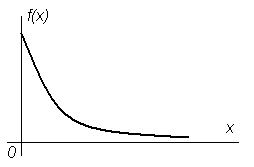
Рисунок 13 График плотности вероятности экспоненциально распределенной случайной величины
Определим основные числовые характеристики этого распределения:
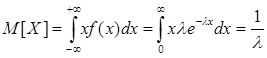 ,
,
т.е. математическое ожидание есть величина обратная параметру закона. Для отыскания дисперсии используем формулу
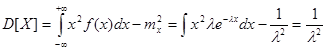 . Откуда средне – квадратичное отклонение будет равно
. Откуда средне – квадратичное отклонение будет равно
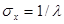 .
.
Вероятность попадания случайной величины на заданный участок, распределенной экспоненциально можно рассчитать, используя формулу
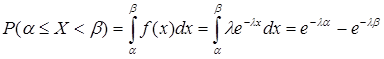 .
.
Дата добавления: 2021-11-16; просмотров: 480;











