Понятие случайной величины. Виды законов распределения.

В зависимости от цели того или иного испытания часто имеют дело с величинами, которые могут принимать те или иные значения, причем заранее неизвестно, какие именно. Такие величины называют случайными.

Случайной называется величина, которая в результате опыта может принять одно и только одно возможное значение, заранее неизвестное и зависящее от случайных обстоятельств.

Примеры случайных величин: число вышедших из строя элементов после 1000 часов работы сложного устройства; величина напряжения в сети в данный момент времени; число покупателей в магазине в момент закрытия.

Различают два основных типа случайных величин: дискретные и непрерывные.

К случайным дискретным величинам относят величины, частные значения которых можно пересчитать, т. е. их число конечно.

У случайных непрерывных величин нельзя пересчитать их частные значения, так как их число бесконечно (они непрерывно заполняют определенный интервал).

Случайные величины обозначают прописными буквами X, Y, Z, а их частные значения – строчными буквами x, y, z.

Случайное событие можно рассматривать как частный случай случайной величины.

Например: событие A – попадание пули в мишень, событие 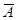- непопадание пули в мишень. Если случайная величина X принимает частное значение x=1, то появляется событие A, а если случайная величина X принимает частное значение x=0, то появляется событие .

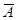Всякое соотношение, устанавливающее связь между частным значением случайной величины и вероятностью ее появления, называют законом распределения.

Если случайная величина X принимает частные значения 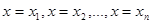с вероятностью 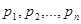, то закон распределения случайной величины запишется в виде соотношений

…………….

…………….

.

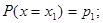
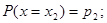
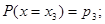
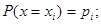
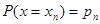К основным математическим формам законов распределения случайной величины относят:

ряд распределения,

многоугольник распределения,

функцию распределения,

плотность распределения.

Ряд распределения применяется для случайных дискретных величин и представляет собой таблицу, в первой строке которой указываются частные значения случайной величины, а во второй – вероятности их появления (таблица 1).

Таблица 1

x				…		…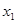
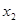
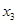
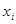
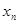
P(X=x)				…		…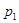

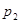
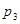
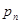
Эта таблица позволяет найти ответы на следующие вопросы.

Какие частные значения может принимать случайная величина?

Какие частные значения случайной величины будут появляться чаще, а какие реже?

По этой таблице можно определить вероятность появления случайной величины в заданных пределах 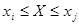, т.е.

.

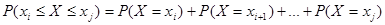Многоугольник распределенияпредставляет собой график, на котором по оси абсцисс откладываются частные значения случайной величины, а по оси ординат – вероятности их появления.

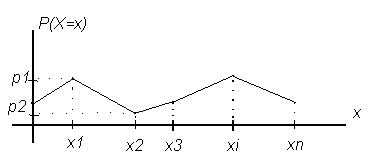
Рисунок 1 Многоугольник распределения

График многоугольника распределения решает те же вопросы, что и ряд распределения.

Ряд и многоугольник распределения не являются универсальными характеристиками случайной величины. Их нельзя построить для случайной непрерывной величины. Поэтому необходима универсальная характеристика, пригодная не только для дискретных, но и для непрерывных величин. Такой характеристикой является функция распределения (интегральная функция) случайной величины, которая обозначается F(x).