Прогнозирование на основе уравнения регрессии

При определении средней квадратической ошибки (дисперсии) прогноза, основанного на линейной модели, исходя из вышеизложенных соображений, необходимо учитывать, по крайней мере, два источника неопределенностей.

Во-первых, естественно полагать, что действительные значения зависимой переменной не будут совпадать с расчетными (прогнозными), так как сама линия регрессии описывает взаимосвязь лишь в среднем, в общем. Отдельные наблюдения рассеяны вокруг нее. Таким образом, наиболее очевидным фактором, во многом определяющим надежность получаемых по уравнению регрессии прогностических оценок, является рассеяние наблюдений вокруг линии регрессии.

Во-вторых, в силу того, что оценивание параметров модели осуществляется по выборочным данным, оценки a и b сами содержат некоторую погрешность. Причем погрешность в значении а приводит к вертикальному сдвигу линии регрессии. В свою очередь, колебание оценки b, связанное с ее выборочным происхождением, приводит к «покачиванию» линии регрессии.

В качестве меры рассеяния наблюдений вокруг линии регрессии принимается такая общераспространенная характеристика, как дисперсия (остаточная дисперсия или дисперсия остатков). Оценка ее (2.13), как известно, равна сумме квадратов отклонений, деленной на число степеней свободы. В данном случае (таблица 6.1), учитывая то, что две степени свободы теряются при определении параметров уравнения прямой, она составит

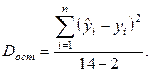
Погрешность в оценке параметров модели также учитывается дисперсиями – дисперсией параметра а и дисперсией параметра b. Для их определения удобно воспользоваться формулами для вычисления коэффициентов линейной регрессии при центрированной независимой переменной, а именно

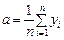и ,

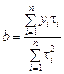где .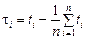

В этом случае параметр а есть выборочное среднее. Оценка дисперсии выборочного среднего при его распределении по нормальному закону представляет собой отношение остаточной дисперсии к общему числу наблюдений, то есть

.

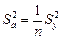Дисперсия параметра b представляет собой отношение остаточной дисперсии к сумме квадратов отклонений (от средней) значений независимой переменной 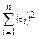с учетом квадрата значения независимой переменной 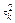(переменной, для которой определяется прогноз):

.

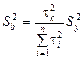Из данного выражения видно, что 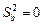в точке .

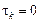Таким образом, оценка дисперсии прогноза, осуществленного на основании линейного тренда,

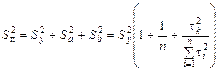
или, переходя к независимой переменной t:

.

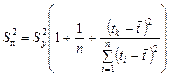При статистической постановке прогнозной задачи

,

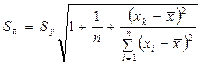где 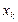– заданное прогнозное значение;

а 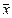– среднее значение независимой переменной x.

Поскольку сумма квадратов отклонений в рассматриваемом примере равна 1396,

то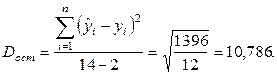

Доверительный интервал уменьшается при увеличении продолжительности наблюдения (периода основания прогноза, периода ретроспекции) и растет с увеличением периода упреждения прогноза [7, 8].

Определим доверительный интервал в рамках рассмотренного выше примера (таблица 6.1). Так как линейное уравнение регрессии содержит два оцениваемых параметра, а число наблюдений 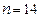, то число степеней свободы при расчете 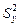составит 14–2=12. Необходимые для расчета среднего квадратического отклонения показатели разности между фактическими и расчетными значениями уровней представлены в таблице 6.2.

Таблица 6.2 – Расчет отклонений от линейного тренда

t
yt
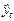
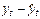
			-3	-10	-10					-4	-2	-5		-19

Учитывая, что прогноз осуществляется для 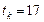(на 2009 г.),

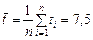и .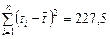

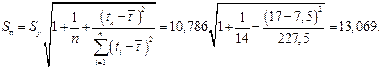
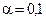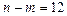При доверительной вероятности 0,9, и значение t-статистики Стьюдента равно 1,78 и 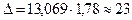. Таким образом, интервальный прогноз 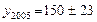изделий.

Уравнения трендов иногда определяют на основе относительно коротких динамических рядов. Естественно, что в этом случае возникает опасность того, что доверительные интервалы для линии тренда, а следовательно, и для прогностических оценок окажутся весьма широкими. Поэтому, задавшись некоторыми ограничениями на размер ошибки прогноза или ошибки уравнения тренда, можно найти минимальное число наблюдений, при котором поставленное условие будет соблюдено. Так, например, уравнение, определяющее средние квадратические ошибки линии тренда ( 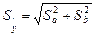), в общем виде можно представить как 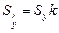, где k – некоторая функция числа наблюдений и периода упреждения. В случае линейного тренда выражение для функции k можно определить из следующих соображений [7].

Величина k характеризует собой отношение средних квадратических ошибок

.

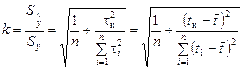Так как последовательность значений t_i составляет натуральный ряд чисел, то

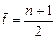и

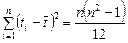
(величины, характеризующие разности 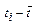, являются членами ряда с равноотстоящими элементами). Далее, величина 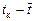характеризует расстояние z от середины динамического ряда до точки на оси времени, для которой делается прогностическая оценка. следовательно,

.

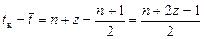Таким образом,

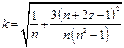
и представляет собой среднюю квадратическую ошибку уравнения, измеренную в единицах среднего квадратического отклонения от тренда. Этой величиной можно воспользоваться в качестве некоторого критерия погрешности и, исходя из ее значения, определить минимально необходимое число наблюдений при заданном периоде упреждения. Допустим, что средняя квадратическая ошибка уравнения не должна превышать 1 при z=1. Тогда

,

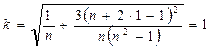откуда .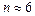

Определение доверительных интервалов полиномов невысоких степеней связано с более объемными по содержанию выводами зависимостей. Эти выводы широко представлены в специальной литературе, поэтому в целях более компактного изложения материала далее приводятся лишь конечные выражения.

Дисперсия прогноза, основанного на квадратичной модели определяется выражением:

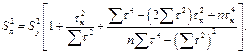
Дисперсия прогноза, основанного на кубичной параболе:

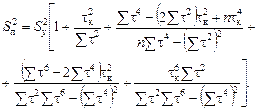
Простое сопоставление подкоренных выражений приведенных формул говорит о том, что при одной и той же величине доверительный интервал тем шире, чем выше степень полинома, характеризующего тренд. Это и понятно, поскольку дисперсия уравнения тренда определяется как взвешенная сумма дисперсий соответствующих параметров уравнений. И все-таки, если тренд лучше описывается кривой более высокого порядка, то соответственно среднеквадратическая ошибка будет, ниже и, следовательно, доверительный интервал уже, чем, скажем, при линейном тренде.

Таким образом, в прогнозных расчетах по уравнению регрессии определяется предсказываемое (y_пр) значение как точечный прогноз 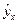при x = x_пр, т.е. путем подстановки в уравнение регрессии соответствующего значения x. При этом необходимо правильно выбирать интервал прогноза (период упреждения).