Оценка точности и достоверности прогноза

Очевидно, что точность прогноза тем выше, чем меньше величина ошибки, которая представляет собой разность между прогнозируемым и фактическим значениями исследуемой величины.

Вся проблема состоит в том, чтобы вычислить ошибку прогноза, так как фактическое значение прогнозируемой величины станет известно только в будущем. Следовательно, методы оценки точности по уже свершившимся событиям (апостериорные) не имеют практической ценности, так как являются лишь констатацией факта. При разработке прогноза оценку его точности требуется производить заранее (априорно), когда истинное значение прогнозируемой величины еще не известно. Как же поступать в этих случаях? Дискуссии в специальной литературе отмечают эти трудности, в итоге все предложения так или иначе связаны с определением доверительного интервала на основе статистического выборочного метода. При этом точность прогноза оценивается величиной доверительного интервала для заданной вероятности его осуществления, а под достоверностью понимают оценку вероятности осуществления прогноза в заданном доверительном интервале. Следовательно, точность прогноза выражается с помощью вероятностных пределов фактической величины от прогнозируемого значения.

Следует отметить, что точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, – явление маловероятное, этому виной следующие источники погрешности:

1) выбор формы кривой (порядка полинома и так далее), характеризующей тренд, содержит элемент субъективизма. Во всяком случае, часто нет твердой основы для того, чтобы утверждать, что выбранная форма кривой является единственно возможной или тем более наилучшей для экстраполяции в данных конкретных условиях;

2) оценивание параметров кривых (иначе говоря, оценивание тренда) производится на основе ограниченной совокупности наблюдений, каждое из которых содержит случайную компоненту. В силу этого параметрам кривой, а следовательно, и ее положению в пространстве свойственна некоторая неопределенность;

3) тренд характеризует некоторый средний уровень ряда на каждый момент времени. Отдельные наблюдения, как правило, отклоняются от него в прошлом. Естественно ожидать, что подобного рода отклонения будут происходить и в будущем.

Погрешность, связанная со вторым и третьим ее источниками, может быть отражена в виде доверительного интервала (рисунок 6.1) прогноза при принятии допущений о свойстве ряда.

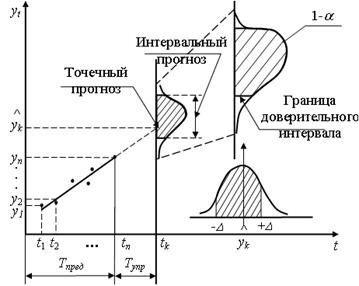
Рисунок 6.1 – Формирование доверительного интервала прогноза

По теории математической статистики при условии, что случайные ошибки имеют нормальное распределение, величины разброса событий (доверительный интервал) при соответствующих вероятностях имеют следующие диапазоны:

для ;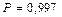

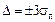для ;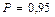

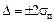для ,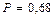

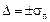где 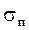– среднеквадратическая ошибка прогноза.

Однако полученные в ходе статистического оценивания параметры не свободны от погрешности, связанной с тем, что объем информации, на основе которой производилось оценивание, ограничен и в некотором смысле эту информацию можно рассматривать как выборку. Строго говоря, так как величина 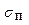является среднеквадратичной ошибкой (СКО) «генеральной совокупности» величин y_i, достигаемой лишь при i®¥, то необходимо вводить поправку на недостаточный объем выборки. С этой целью в формулу вычисления доверительных границ интервала необходимо ввести коэффициент – значение t-статистики Стьюдента и оперировать выборочной СКО:

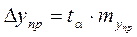, (6.5)

где t_α – так называемый коэффициент доверия, определяемый с помощью таблиц распределения Стьюдента (при уровне значимости α =0,05 и числу степеней свободы n-m);

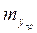– выборочная среднеквадратическая ошибка прогноза (тренда);

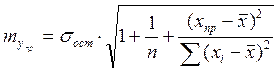. (6.6)

Таким образом, определение точности и достоверности прогноза заключается в определении доверительного интервала:

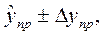
(6.7)

Величину 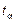выбирают из таблиц в зависимости от α ( 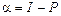, где Р – заданная вероятность осуществления прогноза) и числа степеней свободы v ( 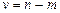, где n – число уровней динамического ряда, m – число параметров уравнения тренда; для линейного тренда ).

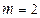Обоснование периода упреждения.Период упреждения (T_упр)– это период времени, на который разрабатывается прогноз. Уравнения трендов иногда определяют на основе относительного коротких динамических рядов. Считается, что период упреждения прогноза не должен превышать 1/3 периода основания прогноза, либо должен быть достаточен для разработки прогноза. Иначе, доверительный интервал для линии тренда, а, следовательно, и для прогностических оценок окажется весьма широким. Задавшись некоторыми ограничениями на размер ошибки прогноза или ошибки уровня тренда, можно найти минимальное число наблюдений, при котором поставленное условие будет соблюдено.

Вопросы для самопроверки по 6 разделу

1. Что характеризует детерминированная компонента в уравнении тренда?

2. Что отражает стохастическая компонента в уравнении тренда?

3. В чем состоит задача прогноза?

4. Что является первым этапом экстраполяции тренда?

5. В чем состоит сущность метода наименьших квадратов?

6. Какие функции чаще всего используются в качестве модели тренда в практических исследованиях?

7. Что характеризует начальный (свободный) коэффициент в уравнении линейного тренда?

8. Что понимают под точностью прогноза?

9. Что понимают под достоверностью прогноза?

10. Какие источники погрешности при построении тренда Вы знаете?

11. Что такое доверительный интервал?

12. Зачем в формулу вычисления доверительных границ интервала вводят коэффициент t-статистики Стьюдента?

13. Какие источники неопределенности необходимо учитывать при определении средней квадратической ошибки прогноза, основанного на линейной модели?

14. Что чаще всего принимается в качестве меры рассеяния наблюдений вокруг линии регрессии?

15. Как происходит оценка дисперсии прогноза?

16. Как ведет себя доверительный интервал при увеличении продолжительности наблюдения?

17. Как меняется доверительный интервал при увеличении периода упреждения прогноза?

ЗАКЛЮЧЕНИЕ

Как и любая другая наука, Эконометрика не стоит на месте. Постоянно развиваются и совершенствуются методы эконометрических исследований социально-экономических явлений. В свою очередь эконометрические методы дают основу для развития новых подходов комплексного анализа и прогноза развития сложных объектов, систем и явлений.

В данном пособии основное внимание уделено раскрытию сущности базовых понятий эконометрики. Детально рассмотрены процедуры эконометрического исследования на основе парной линейной и нелинейной регрессии, а также широкоиспользуемые подходы на основе множественной линейной регрессии.

Разделы, касающиеся прикладных аспектов эконометрических исследований (исследования временных рядов и др.), содержат сведения об основных особенностях применения подходов корреляционно-регрессионного анализа и прогнозирования применительно к анализу функционирования сложных социально-экономических систем (явлений или объектов). Более подробно данный материал изложен в предложенном списке источников литературы, используя который обучаемый (исследователь) может самостоятельно дополнить и углубить знания по интересуемой тематике.