ЦЕНТРОБЕЖНЫЕ НАСОСЫ. Основы подобия
Движение жидкости в межлопастных каналах ЦН имеет сложный характер. Поэтому при решении уравнений движения жидкости принимают ряд допущений. Исходя из сложности движения жидкости, при создании ЦН в частности и лопастных насосов вообще с лучшими эксплуатационными качествами наряду с теоретическими расчетами большое значение приобретают экспериментальные исследования и их обобщение.
Обобщение результатов проводимых испытаний (например, моделей) и перенос их на другие насосы (например, натурные насосы) осуществляются на основании положения о механическом подобии потоков жидкости в них. Для этого необходимо соблюдение трех видов подобия: геометрического, кинематического, динамического. Другими словами, использование обобщенной информации испытаний модельных ЦН при проектировании (создании) натурных осуществляется с помощью теории о механическом подобии потоков жидкости.
Конкретные случаи практического использования положений о механическом подобии: пересчет параметров одного насоса на параметры другого при условии геометрического подобия их проточных частей и 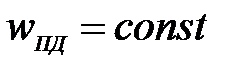 ; пересчет параметров насоса с одной частоты вращения на другую.
; пересчет параметров насоса с одной частоты вращения на другую.
При проектировании насосов широко используется моделирование. При этом модели должны быть изготовлены согласно требованиям законов подобия.
Сущность геометрического подобия. В его основу положена пропорциональность сходственных линейных размеров геометрических параметров натурного и модельного насосов. Используя в качестве таких параметров соответственно для натуры и модели высоту лопасти (например, для ОН lн, lм) и наружный диаметр РК (например, для ЦН D2H, D2m), можно записать уравнение геометрического подобия
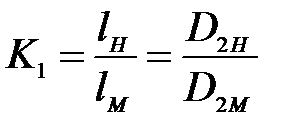
| (1) |
Коэффициент K1 принято называть геометрическим масштабом или масштабом длины.
Сущность кинематического подобия. Прежде всего у натурного и модельного насосов должно быть соблюдено геометрическое подобие и выдержана одинаковая ориентация модельного и натурного насосов относительно потока жидкости. Только при этих условиях можно рассматривать кинематическое подобие. В основу такого подобия положено прохождение сходственными частицами потоков жидкости (модели и натуры) подобных путей в пропорциональные отрезки времени. Используя скорости потоков жидкости для натурного и модельного насосов, можно записать уравнение кинематического подобия
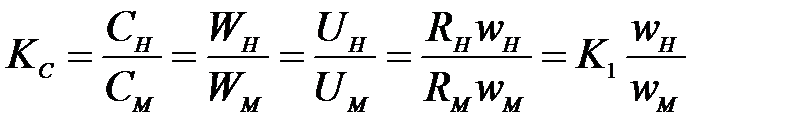
| (2) |
Коэффициент КC принято считать масштабом скоростей.
Сущность динамического подобия.Обязательным условием такого подобия должно быть соблюдение геометрического и кинематического подобия у модельного и натурного насосов. В его основу положено постоянство отношения сил, приложенных к выделенным элементарным объемам в сходственных точках потоков жидкости.
Для выполнения условия динамического подобия ЦН в частности и лопастных насосов вообще необходимо равенство двух критериев: Рейнольдса (Re) и Струхаля (Sh). В том случае, когда насос и его модель перекачивают одну и ту же жидкость, для их подобия достаточно соблюдения только условий, предусмотренных равенствами (1) и (2). Исходя из сказанного, можно записать уравнение динамического подобия при условии, что жидкость несжимаемая и вязкая, а ее движение неустановившееся:
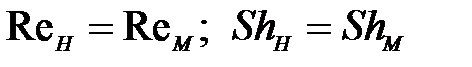
| (3) |
Критерий подобия вообще характеризует отношение сил различной природы, действующих в движущейся жидкости. В частности, критерий Рейнольдса характеризует отношение сил инерции к силам вязкости, а критерий Струхаля — сил инерции, возникающих от переноса частиц, к силам, возникающим от нестационарности их движения:
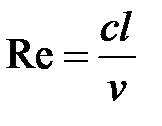
|
где с — скорость движения частицы жидкости; l — длина прохождения ее пути; 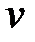 — коэффициент кинематической вязкости;
— коэффициент кинематической вязкости;
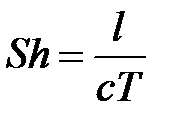
|
где l — длина пути; с — скорость; Т — время.
Критерий Струхаля, другими словами, характеризует подобие инерционных сил при неустановившемся движении жидкости. Условие установившегося движения жидкости 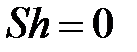 . В этом, случае
. В этом, случае 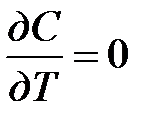 .
.
Примеры использования теории подобия применительно к ЦП. Уравнения подобия связывают основные параметры (Q, N, H) натурного и модельного ЦН и по известным их значениям модельных насосов позволяют определить параметры натурных насосов (QH, NH, HH).
Подача натурного насоса
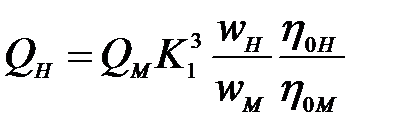
| (4) |
Отношение 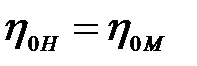 учитывает изменение объемных потерь, обусловленных изменением относительных значений зазоров, при существенном изменении масштаба.
учитывает изменение объемных потерь, обусловленных изменением относительных значений зазоров, при существенном изменении масштаба.
Мощность натурного насоса
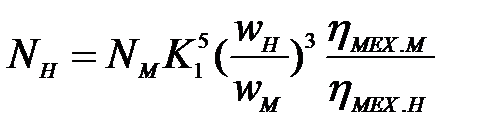
| (5) |
Отношение учитывает изменение относительной величины механических потерь в подшипниках и сальниках. Напор натурного насоса
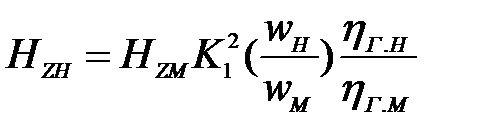
| (6) |
Отношение 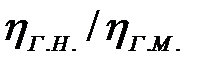 учитывает изменение гидравлических потерь в зависимости от числа Re и геометрического масштаба.
учитывает изменение гидравлических потерь в зависимости от числа Re и геометрического масштаба.
Если рассматривается один насос и к нему применяются указанные уравнения подобия, то в этом случае 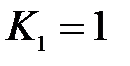 . В области режимов работы насоса
. В области режимов работы насоса 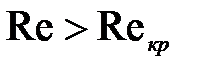 объемные и гидравлические потери постоянны, поэтому и КПД равны. Исходя из этого, по известным (опытным) значениям параметров Q1, H1, N1 и на одном режиме w1 можно определить аналогичные параметры на другом режиме работы wi по уравнениям подобия:
объемные и гидравлические потери постоянны, поэтому и КПД равны. Исходя из этого, по известным (опытным) значениям параметров Q1, H1, N1 и на одном режиме w1 можно определить аналогичные параметры на другом режиме работы wi по уравнениям подобия: 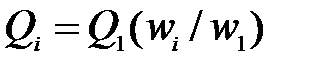 ;
; 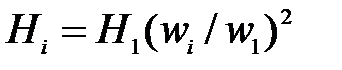 ;
; 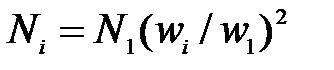 (приближенно, без учета изменения механических потерь).
(приближенно, без учета изменения механических потерь).
На подобных режимах работы насоса сохраняются постоянными отношения: 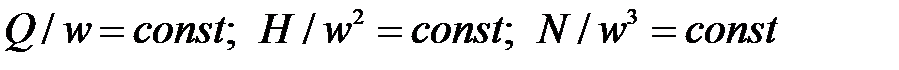 .
.
Дата добавления: 2018-05-10; просмотров: 1425;











