Характеристика сети и рабочий режим системы. Устойчивость работы ЦН в системе

Согласно уравнению Бернулли для реальной жидкости, движущейся по ГС, ее напор определяется по формуле

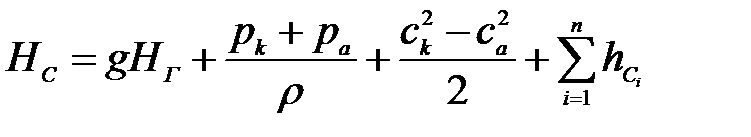
(16)

где

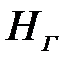— геометрическая высота подъема жидкости в ГС;

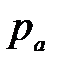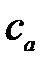и — давление и скорость в приемной емкости;

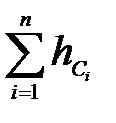—сумма потерь энергии на всех участках ГС;

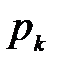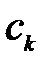и — давление и скорость в напорной емкости.

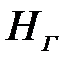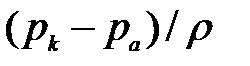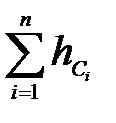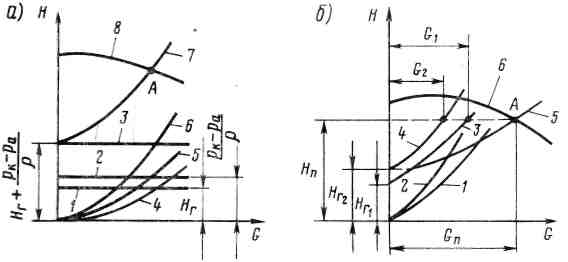
Первые два слагаемых формулы (16) представляют собой статический напор ГС, два других — динамический. Не зависящими от расхода в ГС являются и ,поэтому они выражаются прямыми 1 и 2 (рис. 19, а). Общая ХС будет сумма ординат (прямая 3 на рис. 19, а). Зависящие от расхода ГС: ; 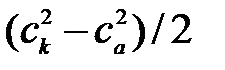. Они представляются параболами второй степени (кривые 4, 5 на рис. 19, а). Их суммирование выражается кривой 6 на рис. 19, а. Полная ХС получается путем суммирования ординат линий 3 и 6 (кривая 7). Точка пересечения ХС и НХ насоса (точка А) определяет рабочий режим ГС.

При работе одного насоса на несколько параллельных ветвей принцип нахождения рабочей точки остается тем же, но с некоторым усложнением. Например, работа пожарного насоса (рис. 19, б).

Рис. 19. К построению характеристик гидравлической сети и определению рабочего режима системы

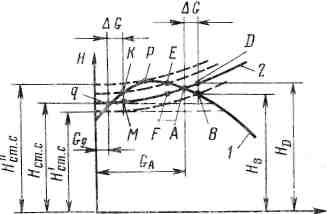
Физическая сущность устойчивости работы насоса в составе ГС видна из рассмотрения их совместных характеристик 1 и 2 (рис. 20).

Рис. 20. К определению устойчивости работы насоса в составе ГС

Условием материального и энергетического балансов ГС будут точки А и q. Допустим, что вследствие кратковременного падения давления в напорной емкости расход жидкости возрос, точка А переместилась вверх по линии 2 и заняла положение точки D. Произошли приращение расхода жидкости в системе 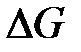, снижение статического напора сети до величины и перемещение ХС вниз параллельно исходной. При этом рабочей точкой системы стала точка В. После устранения источника возмущения ХС переносится вверх на прежнее место, расход жидкости в сети будет 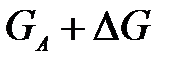, а напор — 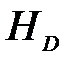. При таком расходе насос может развить напор, только соответствующий точке В (кривая 1). Значит, появится несоответствие напоров сети и насоса, т. е. 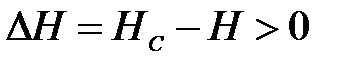. Будет иметь место недостаток энергии в системе, который приведет к снижению скорости потока и соответственно расхода до 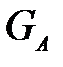.Таким образом, равновесие системы восстановится в исходной точке А. В случае временного повышения давления в напорной емкости 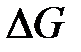будет иметь отрицательное значение, появится избыток энергии в системе 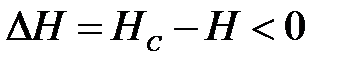, увеличатся скорость потока и расход в сети. Произойдет восстановление равновесия системы. Иная картина получается на другой ветви характеристик насоса и сети (точка q). При временном возрастании статического напора имеем:

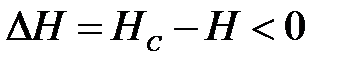
Анализ случаев 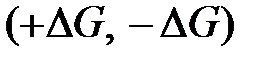показывает, что равновесие системы насос — сеть будет устойчивым, когда 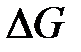и имеют один знак, т. е.

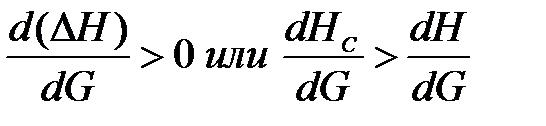
(17)

Неравенства (17) выполнимы при работе насоса на нисходящей и восходящей ветвях характеристики.

Таким образом, создается впечатление, что для обеспечения устойчивой работы системы насос — сеть необходимыми условиями являются: 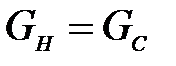и 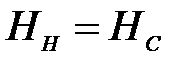и неравенства (17). В некоторых случаях эти условия необходимы, но не всегда достаточны.