Работа силы на криволинейном участке

Рассмотрим общий случай нахождения работы переменной силы, точка приложения которой движется по криволинейной траектории. Пусть точка М приложения переменной силы 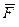движется по произвольной непрерывной кри­вой. Обозначим через 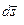вектор бесконечно малого перемещения точки М. Этот вектор направлен по касательной к кривой в ту же сторону, что и вектор скорости.

Элементарной работой переменной силы 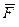на бесконечно малом переме­щении 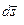называется скалярное произведение векторов 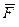и :

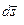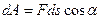, (6.11)

где a - угол между векторами 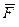и .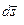

То есть элементарная работа силы равна произведению модулей векторов силы и бесконечно малого перемещения, умноженному на косинус угла между этими векторами.

Разложим вектор силы 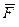на две составляющие: 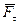- направленную по каса­тельной к траектории – и 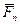– направленную по нормали (рис. 6.2). Линия дей­ствия силы 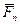перпендикулярна касательной к траектории, по которой дви­жется точка, и ее работа равна нулю. Тогда:

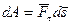. (6.12)

Для того, чтобы вычислить работу переменной силы 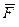на конечном участке кривой от a до b, следует вычислить интеграл от элементарной работы:

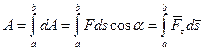. (6.13)

Теорема. Работа равнодействующей системы сил на некотором пути равна сумме работ составляющих сил на том же пути.

Доказательство:

Пусть точка М приложения системы сил { 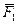, , 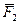,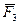… 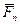} перемещается из положения М₀ в положение М₁; кроме того, пусть

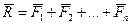, (6.14)

то есть 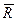– равнодействующая системы сил (рис. 6.3).

Вычислим элементарную работу силы 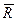. Для этого умножим равенство (6.14) скалярно на :

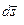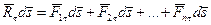, (6.15)

то есть элементарная работа равнодействующей равна сумме элементарных работ составляющих.

Представляя модули F₁, F₂, F₃, ... F_n как функции s и интегрируя выражение (6.15) в соответствующих пределах, получим:

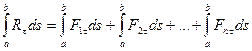. (6.16)

Поскольку 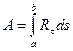, , 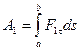... , 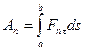, окончательно имеем:

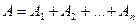, (6.17)

что и требовалось доказать.

Рис. 6.3

Лекция 7

Мощность

Две различные силы могут совершать одну и ту же работу за разные проме­жутки времени. Характеристикой, позволяющей оценить быстроту совершения работы, является мощность.

Мощностью называется работа, произведенная в единицу времени:

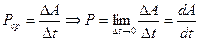. (7.1)

Если в любые равные промежутки времени производится одна и та же работа, то мощность может быть вычислена по формуле:

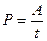. (7.2)

В Международной системе единиц (СИ) в качестве единицы мощности принят ватт – работа в один джоуль, произведенная за одну секунду .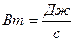

Если в формуле (7.1) вместо элементарной работы DА подставить ее выра­жение из (6.12), получим еще одно соотношение для вычисления мощности:

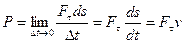. (7.3)

При эксплуатации любой машины часть потребляемой ею мощности тра­тится на преодоление различных сопротивлений, то есть на совершение полез­ной работы расходуется только часть потребляемой мощности. Отношение по­лезной мощности (работы) ко всей потребляемой мощности (работе) называется коэффициентом полезного действия (КПД) машины:

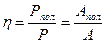. (7.4)

КПД характеризует рациональность использования потребляемой мощно­сти. Поскольку полностью избавиться от потерь мощности при эксплуатации машины невозможно, КПД любой машины меньше единицы.