Смешанное соединение резистивных элементов

При наличии в цепи только одного источника ЭДС внешнюю по отношению к источнику часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение элементов.

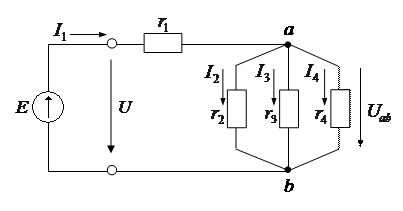
В приведенной схеме несколько резистивных элементов, которые соединены параллельно.

Расчет смешанного соединения нужно начинать с определения эквивалентной проводимости g каждого параллельно соединенного резистивного элемента, то есть подключенных к одной и той же паре узлов. В схеме

;

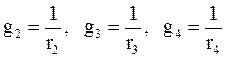эквивалентная проводимость равна:

.

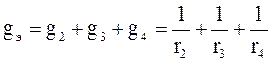После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением 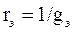получается эквивалентная схема с последовательным соединением двух резистивных элементов r₁ и r_э.

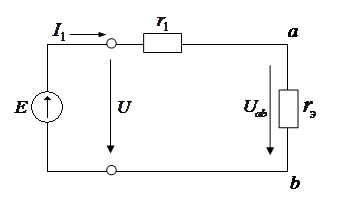
Ток в неразветвленной части цепи равен:

.

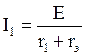Чтобы определить токи в параллельных ветвях (токи I₂, I₃, I₄), нужно сначала вычислить напряжение между узлами a и b:

.

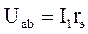И далее, по закону Ома определяем токи в ветвях:

.

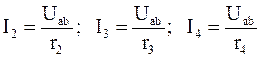Таким образом получены значения расчетных величин заданной цепи.

Метод двух узлов

Часто исследуемая электрическая цепь содержит только два узла или легко может быть преобразована в подобную цепь. Наиболее простым методом расчета в этом случае является метод двух узлов (узлового напряжения).

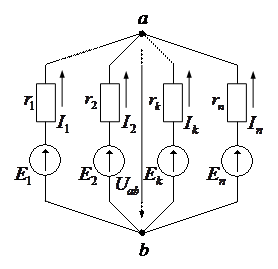
Так как ветви между узлами a и b соединены параллельно, то разность потенциалов между этими узлами можно выразить через ЭДС E_k, ток I_k и сопротивление r_k. По обобщенному закону Ома ток в k-ой ветви равен:

,

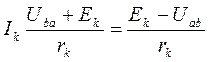откуда

,

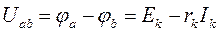где 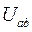– узловое напряжение цепи.

На основании этих выражений можно рассчитать ток в k-ой ветви:

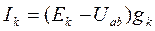, (1)

где 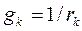– проводимость k-ой ветви.

В приведенном примере принято, что все ЭДС направлены к одному из узлов цепи (к узлу а) и положительное направление каждого тока совпадает с направлением ЭДС в ветви. В действительности некоторые ЭДС могут быть направлены к узлу b. В этом случае при расчете токов в ветвях с теми же положительными направлениями (к узлу а) значения ЭДС, действующих к узлу b, должны быть записаны со знаком минус.

По первому закону Кирхгофа алгебраическая сумма токов в узле равна нулю:

.

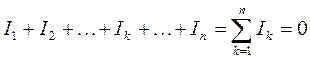Тогда из (1) имеем:

.

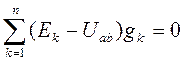Отсюда видно, что узловое напряжение 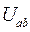может быть определено через параметры элементов цепи:

,

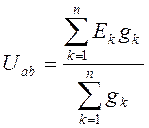здесь со знаком плюс записываются ЭДС, действующие к узлу а.

Зная узловое напряжение 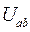, по формуле (1) можно рассчитать ток в любой ветви.