Метод контурных токов
Этот метод может быть применен для расчета любой линейной цепи. Его применение позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Ома и Кирхгофа.
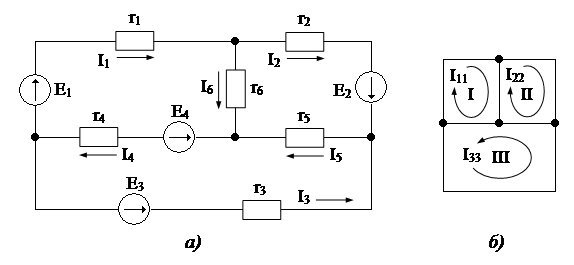
Для расчета методом контурных токов в сложной электрической цепи независимые контуры выбираются так же как и при составлении уравнений по второму закону Кирхгофа, например, рис. б). Затем в каждом контуре произвольно выбирается положительное направление контурного тока (один и тот же ток, протекающий во всех ветвях контура). Расчетную величину – контурный ток обозначим по номеру контура с двойным индексом, например, Ikk. Токи в общих для двух или более контуров ветвях определяются на основании первого закона Кирхгофа как алгебраические суммы соответствующих контурных токов.
Алгебраическая сумма ЭДС всех ветвей, входящих в каждый из выбранных независимых контуров, называется контурной ЭДС Ekk (с двойным индексом по номеру контура), то есть для любого k-го контура
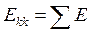 .
.
Арифметическая сумма сопротивлений всех элементов, входящих в каждый из выбранных контуров, называется собственным контурным сопротивлением rkk (с двойным индексом номера контура), то есть для k-го контура
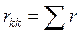 .
.
Арифметическая сумма сопротивлений элементов, находящихся в общих ветвях двух контуров m и l, называется общим сопротивлением этих контуров, причем, очевидно,
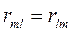 .
.
Для контурных токов, как и для токов в ветвях, должен выполняться второй закон Кирхгофа. Составим систему контурных уравнений для контурных токов по второму закону Кирхгофа для электрической цепи, у которой n независимых контуров:
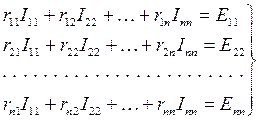
Система уравнений является математической формулировкой метода контурных токов. Так как число контурных токов всегда меньше числа токов в ветвях, то применение этого метода уменьшает число неизвестных величин в решаемой системе уравнений.
Решение системы уравнений может быть записано для контурных токов в общей форме с введением определителей:
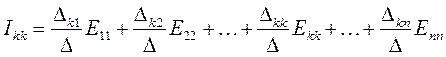 ,
,
где D – определитель системы уравнений, рассчитанный по матрице коэффициентов rkk, а Dkp (p = 1, 2, ..., n) – алгебраические дополнения, получаемые из определителя D посредством вычеркивания k-ой строки и p-го столбца и умножения полученного определителя на (-1)k+p.
Составим уравнения для приведенной схемы. Будем считать, что значения всех ЭДС и сопротивлений элементов заданы. Элементы каждой ветви и токи в ветвях обозначим соответствующими индексами. Составим контурные уравнения, предварительно произвольно выбрав положительные направления обхода контуров.
Для первого контура:
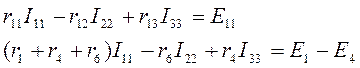
Для второго контура:
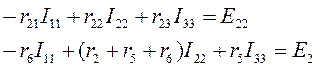
Для третьего контура:
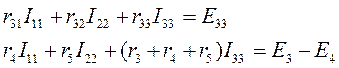
Вычислив значения контурных токов 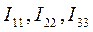 , определим по первому закону Кирхгофа токи во всех ветвях электрической цепи:
, определим по первому закону Кирхгофа токи во всех ветвях электрической цепи:
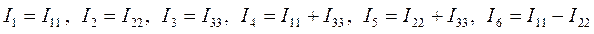 .
.
Дата добавления: 2018-05-10; просмотров: 1219;











