Применение закона Ома и законов Кирхгофа для расчета электрических цепей

При помощи закона Ома и двух законов Кирхгофа можно рассчитать режим работы электрической цепи любой сложности.

Общей задачей расчета является определение токов во всех участках цепи при заданных параметрах элементов цепи и известной конфигурации цепи.

Для составления уравнений по закону Ома и двум законам Кирхгофа следует, прежде всего, выбрать направления токов во всех ветвях рассчитываемой цепи.

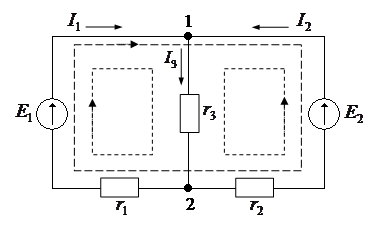
При записи уравнений для узлов цепи по первому закону Кирхгофа необходимо иметь в виду, что число независимых уравнений на единицу меньше общего числа узлов y, то есть нужно составить y – 1 уравнение. Действительно, если составить уравнения для всех y узлов, то ток каждой ветви войдет дважды в уравнение, так как ветвь соединяет два узла с противоположными знаками. При суммировании всех левых частей уравнений, составленных по первому закону Кирхгофа, получается тождественно ноль.

При составлении уравнений на основании второго закона Кирхгофа необходимо также составить независимую систему. В частности, независимая система будет получена, если выбрать контуры так, чтобы каждый следующий содержал хотя бы одну ветвь, не вошедшую в контуры, для которых уже составлены уравнения. Такие контуры называются независимыми.

Число неизвестных токов равно числу ветвей b. Для определения этих токов необходимо составить b независимых уравнений. Так как по первому закону Кирхгофа составляется y – 1 независимых уравнений, то на основании второго закона Кирхгофа должно быть составлено b – (y – 1) уравнений.

Например, для нашей цепи может быть составлено два уравнения по первому закону Кирхгофа (для узлов 1, 2):

.

На основании второго закона Кирхгофа и закона Ома можно составить три уравнения для трех контуров. Для контура 1:

,

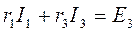для контура 2:

,

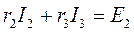для контура 3:

.

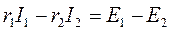Для приведенной схемы число узлов y = 2, то есть по первому закону Кирхгофа нужно составить одно уравнение (2–1=1). Число неизвестных токов равно числу ветвей b = 3. Следовательно, по второму закону Кирхгофа должно быть составлено два уравнения (3–(2–1)=2). Из трех контуров этой цепи в качестве независимых можно взять любую пару контуров.

После совместного решения системы независимых уравнений определяются токи в ветвях цепи. Если для какого-либо тока будет получено отрицательное значение, то из этого следует, что его действительное направление противоположно выбранному.

Применение этого метода для сложных цепей часто требует значительной затраты времени, поэтому желательно, когда это возможно, вести расчеты более простыми методами.