Феноменологический подход
Рассмотрим другой подход для определения коэффициента размножения теплового реактора. Процесс размножения нейтронов в бесконечной мультиплицирующей среде можно оценить количественно, если проследить за судьбой вторичных нейтронов, рождающихся в результате деления горючего.
Итак, пусть у нас имеется однородная бесконечная размножающая среда, состоящая из смеси горючего (например, 235U), порогового нуклида (238U) и замедлителя. Рассмотрим жизненный цикл одного поколения нейтронов при их движении по энергетической шкале, начало которому положено появлению в единице объема среды одного нейтрона деления, появившегося в результате деления ядра 235U тепловым нейтроном. Проследим за судьбой этого нейтрона. В процессе деления рождаются нейтроны, энергия которых может быть как больше, так и меньше порога деления 238U. Нейтроны с энергией 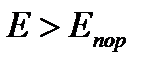 могут вызывать деление ядер 238U. В принципе, мы должны отнести эти родившиеся нейтроны к следующему поколению нейтронов, но поскольку мы договорились относить к одному поколению только те нейтроны, которые появились в результате деления ядер тепловыми нейтронами, то эти вновь родившиеся нейтроны мы должны отнести к этому же поколению. Таким образом, число нейтронов в единице объёма с энергией
могут вызывать деление ядер 238U. В принципе, мы должны отнести эти родившиеся нейтроны к следующему поколению нейтронов, но поскольку мы договорились относить к одному поколению только те нейтроны, которые появились в результате деления ядер тепловыми нейтронами, то эти вновь родившиеся нейтроны мы должны отнести к этому же поколению. Таким образом, число нейтронов в единице объёма с энергией 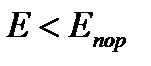 , будет больше числа первоначально родившихся нейтронов деления, за счёт тех нейтронов, которые появились при делении ядер 238U быстрыми нейтронами. Это увеличение числа замедлившихся нейтронов в результате размножения на быстрых нейтронах характеризуется коэффициентом
, будет больше числа первоначально родившихся нейтронов деления, за счёт тех нейтронов, которые появились при делении ядер 238U быстрыми нейтронами. Это увеличение числа замедлившихся нейтронов в результате размножения на быстрых нейтронах характеризуется коэффициентом 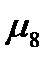 , равным числу быстрых нейтронов, которые замедлились до энергии ниже порога деления 238U, отнесённому к одному быстрому нейтрону, появившемуся при делении 235U тепловыми нейтронами. Таким образом, в результате размножения на быстрых нейтронах за порог деления 238U уйдет
, равным числу быстрых нейтронов, которые замедлились до энергии ниже порога деления 238U, отнесённому к одному быстрому нейтрону, появившемуся при делении 235U тепловыми нейтронами. Таким образом, в результате размножения на быстрых нейтронах за порог деления 238U уйдет 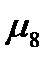 быстрых нейтронов. Эти нейтроны, сталкиваясь с ядрами замедлителя, будут терять свою энергию, то есть замедлятся.
быстрых нейтронов. Эти нейтроны, сталкиваясь с ядрами замедлителя, будут терять свою энергию, то есть замедлятся.
В процессе замедления часть нейтронов претерпевает радиационный захват ядрами 238U, так и не достигнув тепловой энергии. Радиационный захват нейтронов характеризуется коэффициентом 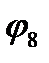 - вероятностью того, что быстрый нейтрон в процессе замедления избежит радиационного захвата на 238U. Захват надтепловых нейтронов при замедлении носит специфический характер. В этой области энергий сечения захвата ядер со средними и большими массовыми числами имеет ярко выраженную резонансную структуру. Поэтому коэффициент
- вероятностью того, что быстрый нейтрон в процессе замедления избежит радиационного захвата на 238U. Захват надтепловых нейтронов при замедлении носит специфический характер. В этой области энергий сечения захвата ядер со средними и большими массовыми числами имеет ярко выраженную резонансную структуру. Поэтому коэффициент 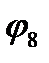 ещё называют вероятностью избежать резонансного захвата. Захват на лёгких ядрах замедлителя в этой области энергий ничтожно мал и в формировании
ещё называют вероятностью избежать резонансного захвата. Захват на лёгких ядрах замедлителя в этой области энергий ничтожно мал и в формировании 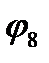 не играет никакой роли.
не играет никакой роли.
Таким образом, до тепловой энергии замедляются 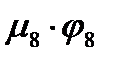 нейтронов. Но даже тогда, когда нейтроны стали тепловыми, не все они поглотятся в уране. Часть их будет захвачена ядрами замедлителя. Если ввести коэффициент
нейтронов. Но даже тогда, когда нейтроны стали тепловыми, не все они поглотятся в уране. Часть их будет захвачена ядрами замедлителя. Если ввести коэффициент 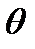 , определив его как вероятность захвата теплового нейтрона топливом, (его называют коэффициентом использования тепловых нейтронов), то ядрами урана будет поглощено
, определив его как вероятность захвата теплового нейтрона топливом, (его называют коэффициентом использования тепловых нейтронов), то ядрами урана будет поглощено 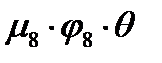 нейтронов.
нейтронов.
Часть нейтронов, поглощенных топливом, вызовут деление ядер 235U, в результате чего появятся нейтроны нового поколения. Их число, приходящееся на один нейтрон, поглощенный в топливе, обозначим через 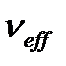 - среднее число нейтронов деления на один захваченный тепловой нейтрон в топливе. Очевидно, что
- среднее число нейтронов деления на один захваченный тепловой нейтрон в топливе. Очевидно, что
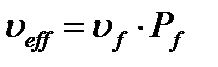 ,
,
где 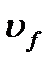 - среднее число нейтронов на акт деления ядра 235U, а
- среднее число нейтронов на акт деления ядра 235U, а
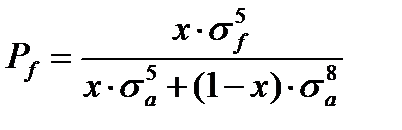
- вероятность того, что при захвате теплового нейтрона топливом, произойдет реакции деления на ядрах 235U..
Таким образом, если пренебречь делением U-235 на замедляющихся нейтронах, то во втором поколении число быстрых нейтронов деления возрастёт до значения 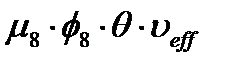 .
.
Коэффициентом размножения в однородной бесконечной среде называют отношение числа нейтронов нового поколения к числу нейтронов предыдущего поколения, так что 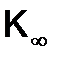 будет выражаться следующим образом
будет выражаться следующим образом
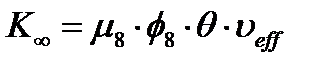 (9)
(9)
Это выражение называется формулой четырёх сомножителей. Подчеркнём ещё раз, что формула четырёх сомножителей описывает размножение нейтронов в сильно замедляющей среде, когда основная доля делений приходится на тепловые нейтроны. Следовательно, она служит для описания размножений нейтронов в реакторе на тепловых нейтронах. В дальнейшем мы получим выражение для каждого сомножителя этой формулы, а начнем с коэффициента размножения на быстрых нейтронах 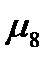 .
.
Дата добавления: 2018-05-10; просмотров: 954;











