Приближение узких резонансов.

Резонанс считается сильным, если

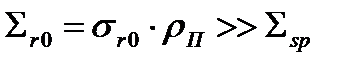(27).

Для определения потока нейтронов в случае сильного резонанса рассмотрим газокинетическое уравнение замедления для однородной бесконечной среды. Для резонансов в области энергий от нескольких эВ до 10 КэВ, можно применить уравнение для асимптотической области энергий, в которую нейтроны попадают, совершив большое число рассеивающих столкновений:

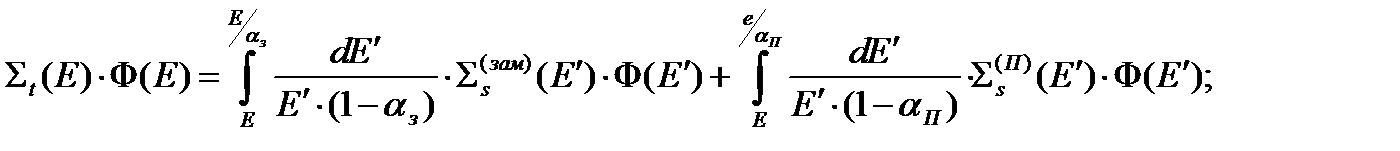(28)

где 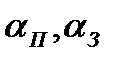- максимальная потеря энергии при рассеянии на ядрах урана и замедлителя соответственно ( 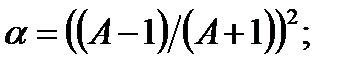). Резонанс считается узким, если ширина резонанса много меньше ступеньки замедления, как для замедлителя, так и для резонансного поглотителя, то есть при выполнении условий

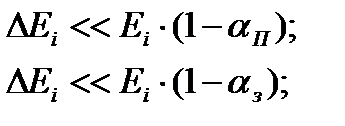(29)

Так как резонанс узкий, то основной вклад в интеграл рассеяния вносит область энергий, далекая от резонансов. Для этих энергий поток нейтронов невозмущен резонансом и описывается распределением Ферми

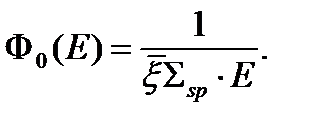(30)

Принимая это во внимание, при интегрировании по энергии в правой части уравнения баланса (28) положим 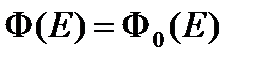во всей области интегрирования. Кроме того, будем считать, что в пределах всей ступеньки замедления 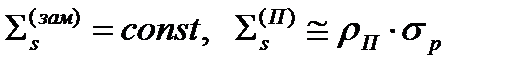. С учетом принятых упрощений, уравнение для определения спектра нейтронов в области резонанса примет следующий вид

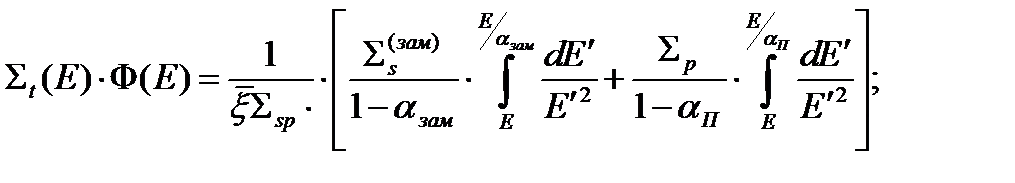(31)

Интегрируя уравнение (31), и учитывая

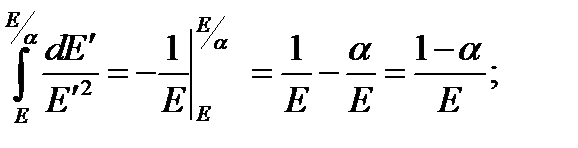
получим

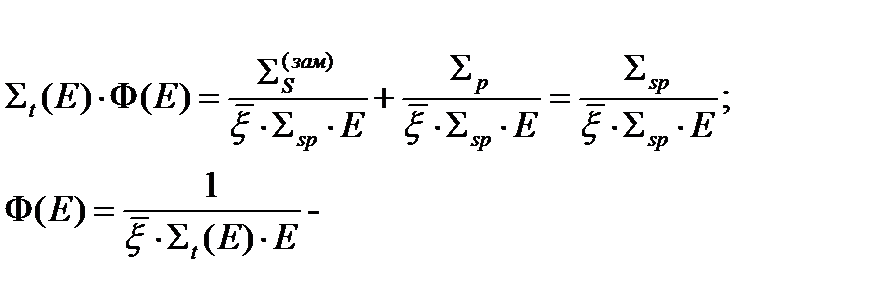(32)

Это решение носит название спектра Вигнера, которое, в отличие от спектра Ферми, описывает спектр нейтронов в области действия сильного резонанса.

Вблизи резонанса S_t(E) резко возрастает, что приводит к падению потока резонансных нейтронов F(E). Снижение потока нейтронов при резонансных энергиях приводит к уменьшению резонансного поглощения, причем тем большему, чем сильнее резонанс. В этом состоит эффект резонансного самоэкранирования или «резонансной блокировки».

РИСУНОК спектра Ферми и Вигнера

Для вычисления вероятности избежать резонансного поглощения на 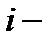том резонансе 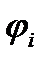, воспользуемся выражением для величины вероятности поглощения, в соответствии с равенством:

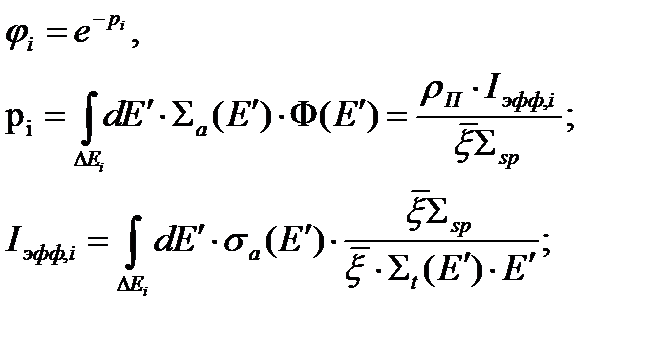(33)

Величина 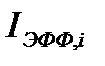носит название эффективного резонансного интеграла. Из выражения (33) следует, что это есть резонансный интеграл от некоторого эффективного сечения резонансного поглощения, которое отличается от истинного резонансного сечения множителем

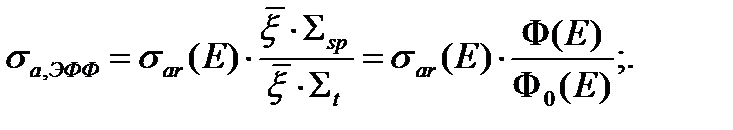(34)

Таким образом, эффективное сечение учитывает депрессию потока нейтронов в сильном резонансе. Пренебрегая интерференционным членом потенциального и резонансного взаимодействия, запишем 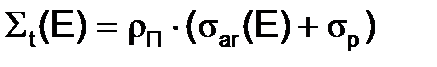и подставим это выражение в (34)

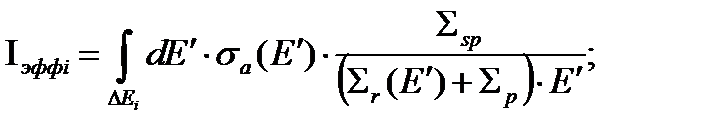(35)

Произведем стандартную замену переменных,

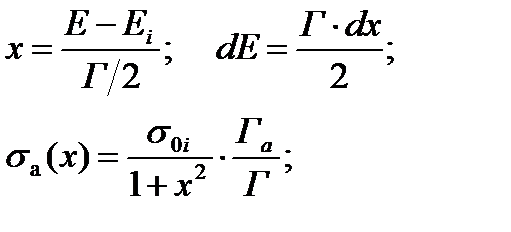
преобразуем выражение для эффективного резонансного интеграла

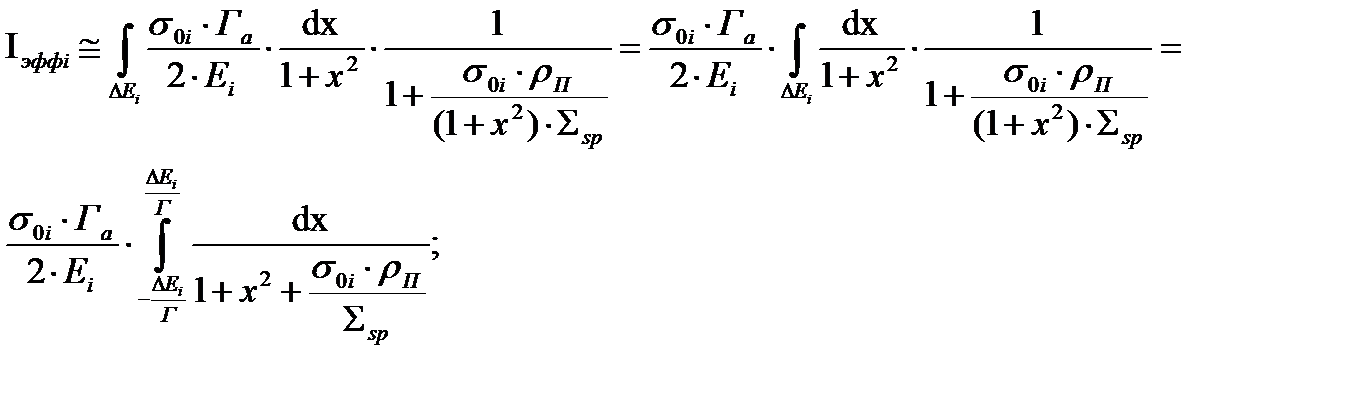(36)

Обозначим

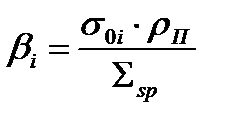(37)

и введем новую переменную интегрирования

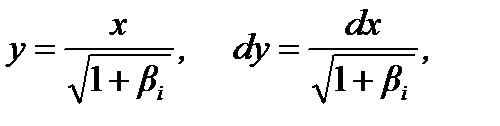
получим

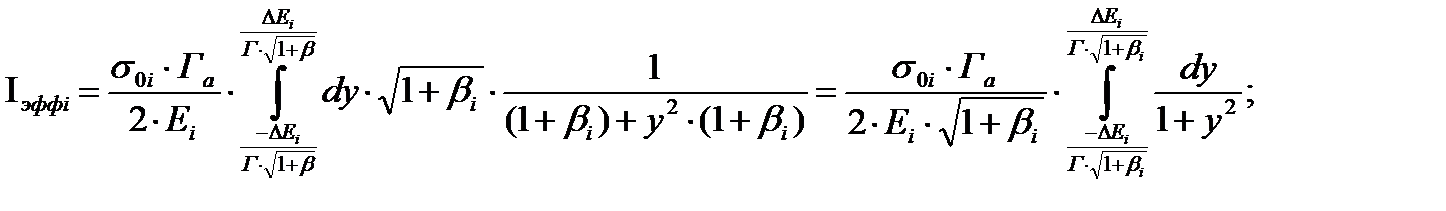
Если |y|>>1, то 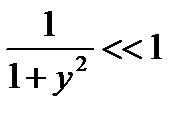. Поэтому, главный вклад в интеграл дадут те значения y, для которых |y|£1, т.е. значения энергии в пределах 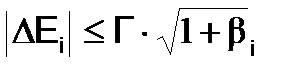. Последнее соотношение позволяет оценить область действия резонанса по энергетической шкале 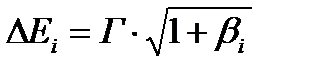. Таким образом, область действия резонанса 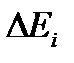оказывается значительно больше истинной ширины резонанса Г.

Так как резонанс изолированный, то пределы интегрирования можно распространить на интервал (-¥,¥), в результате получим окончательное выражение для эффективного резонансного интеграла

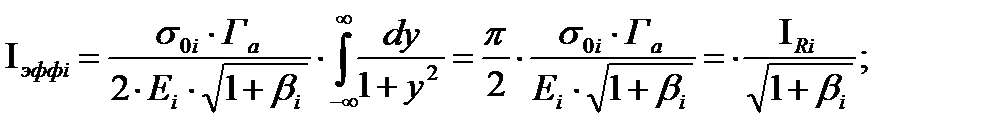(38)

Нетрудно заметить, что 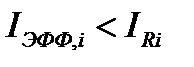. Фактор блокировки 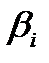зависит от соотношения резонансного и потенциального макросечения взаимодействия. По этому параметру все резонансы можно разделить на две группы: сильные и слабые.

Слабый резонанс

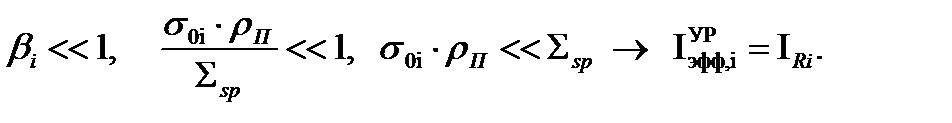(39)

Таким образом, для слабого резонанса эффективный резонансный интеграл совпадает с резонансным интегралом. Это связано с тем фактом, что для слабого резонанса депрессия потока резонансных нейтронов практически отсутствует.

Сильный резонанс

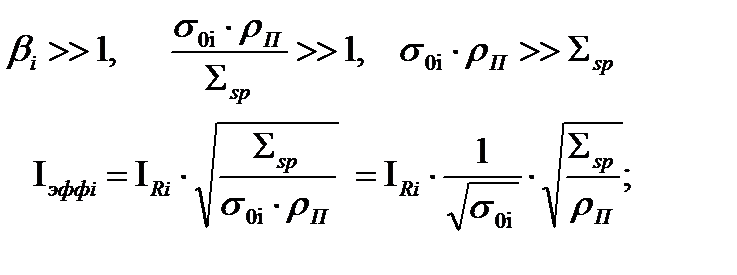(40)

Величина

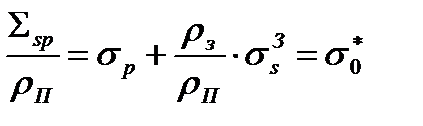(41)

имеет смысл сечения рассеяния гомогенной среды, приходящееся на одно ядро резонансного поглотителя, которая зависит от разбавления 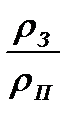. С ростом концентрации поглотителя величины 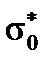и 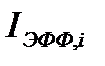уменьшаются, хотя сама вероятность избежать резонансного поглощения растет, однако лишь как 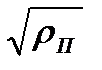, в то время как для слабого поглощения зависимость 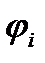от концентрации резонансного поглотителя носит линейный характер.

Эффект самоэкранировки (блокировки) резонанса оказывается весьма большим. Например, для первого резонанса ²³⁸U E_i=6.7 эВ, s_r0=23000 барн, так что при 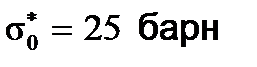I_эффi оказывается в 30 раз меньше I_Ri.

Ширина действия резонанса может быть найдена из условия .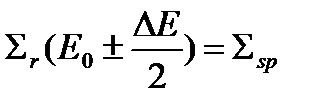

Подставляя выражение для S_r в форме Брейта-Вигнера

.

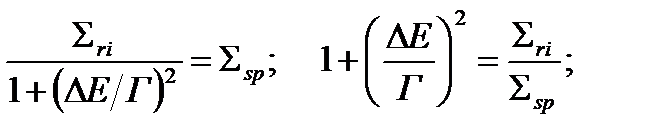Считая 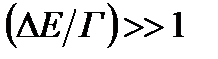, получим

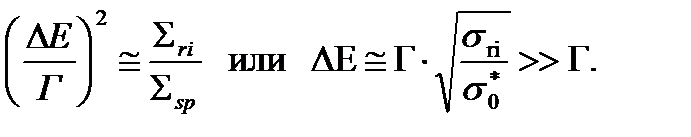(42)

Эффективная ширина сильных резонансов мало меняется от резонанса к резонансу и составляет при небольших разбавлениях ~ 1 эВ.