Многогрупповое приближение.

Размножающие среды, составляющие активные зоны ядерных реакторов, содержат ядра различных элементов. В первую очередь в состав размножающих сред входят топливные компоненты, которые включают как делящиеся нуклиды, такие, как ²³⁵U, ²³⁹Pu, так и пороговые нуклиды ²³⁸U, ²³²Th. Для отвода тепла используются различные теплоносители, состоящие как из легких ядер, такие как H2O, D2O, так и тяжелых, включая расплавленные металлы типа Na или Pb. В большинстве существующих реакторов используется замедлитель нейтронов, состоящие из ядер легких элементов. Для предотвращения контакта теплоносителя с топливом применяются оболочки из различных металлов, а так же различные конструкционные элементы, содержащие ядра Zr, Nb, Fe, Ni и многие другие. Все нетопливные элементы разделим на две группы – замедлители и разбавители. Ядра легких элементов относятся к замедлителям, а ядра тяжелых металлов к разбавителям.

Ввиду того, что ядра различных элементов, входящих в состав размножающей среды, имеют сложные зависимости сечения взаимодействий с нейтронами в различных областях энергий, то получить аналитическое решение уравнения для спектра нейтронов в размножающей среде даже для наиболее простых сред не удается. Для решения этого уравнения применяются различные приближенные методы. Наиболее распространенным методом для бесконечных однородных сред является многогрупповой подход. Суть этого метода заключается в том, чтобы заменить истинные сложные зависимости микросечений от энергии функциями простого вида, например, кусочно-постоянными.

С этой целью весь энергетический диапазон нейтронов в реакторе разбивается точками деления на ряд непересекающихся интервалов (рис.2).

Рис. 2.2 Групповое разбиение энергетического интервала нейтронов

Для определенности рассмотрим разбиение на G непересекающихся интервалов. Пронумеруем получающиеся энергетические интервалы, начиная с верхнего интервала, индексом 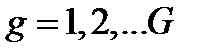. Ширина g-го интервала 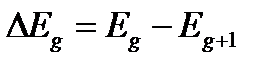. Предполагается, что все микросечения взаимодействия ядер с нейтронами внутри каждого интервала не зависят от энергии и являются постоянными величинами. Конечно, значения этих констант, которые называются групповыми сечениями, отличаются для ядер различных элементов. Нейтроны, энергия которых заключена в пределах g-го интервала, назовем нейтронами группы g. Поскольку все нейтроны внутри группы эквивалентны с точки зрения нейтронно-ядерных взаимодействий, то вместо потока нейтронов в многогрупповом методе используется групповой интегральный поток нейтронов, определяемый соотношением .

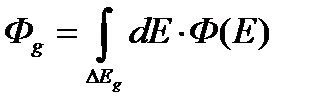Основная проблема многогруппового метода заключается в выборе групповых констант. Для этого используется условие сохранения полного числа процессов любого типа внутри группы. Это условие означает, что полное число процессов 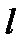-го типа в пределах группового интервала энергий для групповых констант должно быть таким же, как и для истинных макросечений этого типа, то есть должно выполняться соотношение

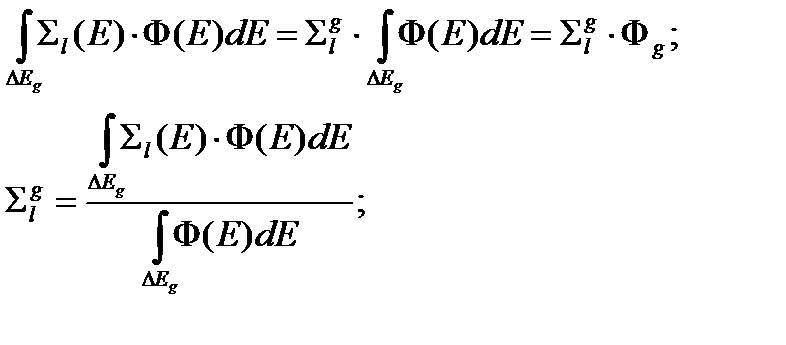
Однако, для того, чтобы получить групповые константы, нам необходимо знать энергетическое распределение нейтронов в группе, Но если мы уже знаем энергетическое распределение в группе, то нам нет необходимости использовать многогрупповое приближение. Выход их этого противоречия заключается в том, что групповые сечения являются дробно линейным функционалами от потока нейтронов. Поэтому, если взять в качестве внутригруппового спектра приближенные решения, то систематическая погрешность в групповых константах от использования приближенного потока будет оказывать существенно меньшее воздействие значение многогрупповых констант. В качестве таких приближенных внутригрупповых спектров используются стандартный набор спектров, таких, как, спектр нейтронов деления, спектр замедления Ферми, спектр Вигнера для групп с резонансным ходом сечения и спектр Максвелла для группы тепловых нейтронов.

Для получения системы многогрупповых уравнений, проинтегрируем исходное уравнение для спектра нейтронов внутри 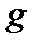-ой группы

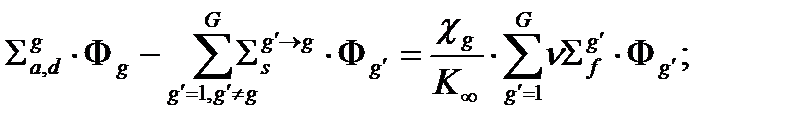(2.4.2)

Здесь введены следующие обозначения:

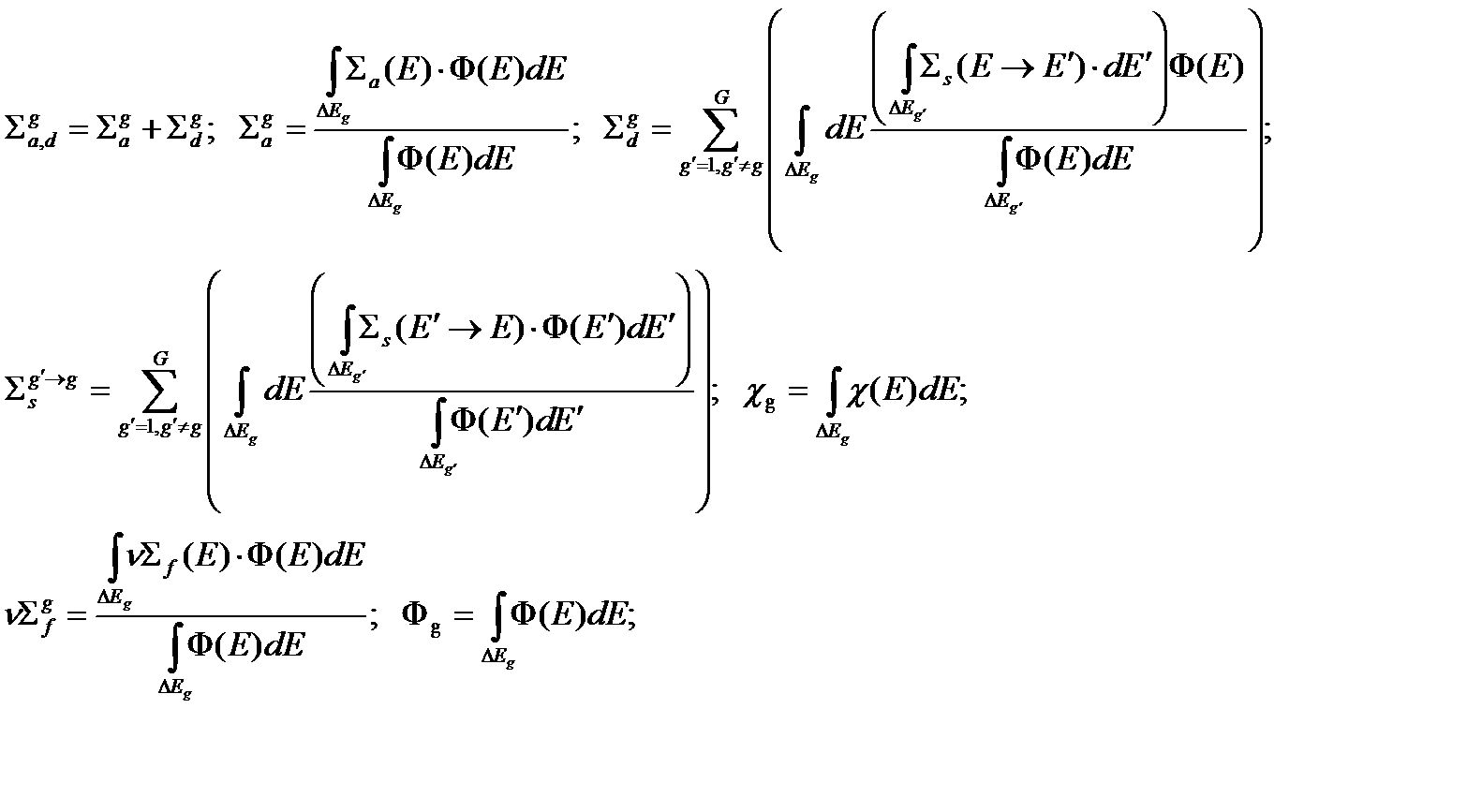
Приведенные величины имеют следующий физический смысл. Величины 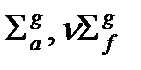- являются групповыми макроконстантами, отвечающие за поглощение нейтронов и их образование соответственно. Величина 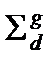отвечает за увод нейтронов в результате рассеяния в другие группы, вообще говоря, как в верхние группы, так и в нижние. Макросечение 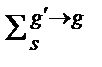связано с переводом нейтронов из любой группы 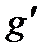в данную группу 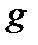за счет реакции рассеяния. И, наконец, величина 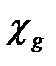определяет долю нейтронов деления попадающих в рассматриваемую группу .

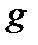Использование многогруппового приближения превращает интегральное уравнение для спектра нейтронов в систему однородных линейных алгебраических уравнений (2.4.2), называемых в дальнейшем системой многогрупповых уравнений. В общем случае система уравнений (2.4.2) предполагает возможность перевода нейтронов за счет рассеяния из нижней группы g^¢ в верхнюю группу g, то есть когда 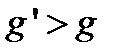. Это означает, что процесс рассеяния нейтрона происходит с увеличением его энергии. Такая ситуация имеет место при рассеянии тепловых нейтронов с ядрами среды, поскольку в этом случае средняя энергия нейтронов сравнима со средней энергий теплового движения ядер среды (процесс термализации нейтронов). 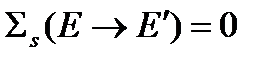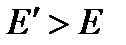В том случае, когда все тепловые нейтроны объединены в одну группу, то возможны только такие переводы нейтронов, при которых их энергия только уменьшается, то есть при , или в групповых обозначениях 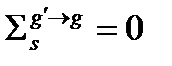когда 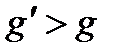. В этом случае система многогрупповых уравнений будет иметь нижне-треугольный вид (2.4.3).

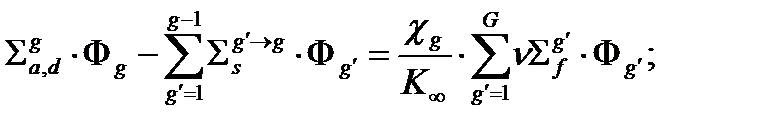(2.4.3)

Рассмотрим физический смысл отдельных членов полученной системы уравнений. Первый член описывает поглощение и увод нейтронов из группы g во все нижележащие группы в результате их рассеяния (g^¢>g). Второй член описывает перевод нейтронов из всех вышележащих групп g^¢ в данную группу g ( 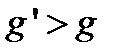). Третий член определяет количество нейтронов, деления, которые попала в группу g непосредственно при делении ядер.

Поскольку система уравнений (2.4.3) однородная, то применим ту же самую нормировку источника деления на один нейтрон, то есть из всего многообразия решений выберем то из них, для которого выполнено условие

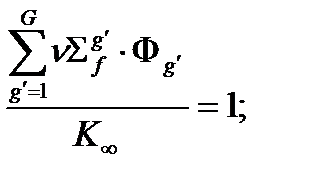
В результате такой нормировки получим систему линейных однородных уравнений многогруппового приближения (2.4.4)

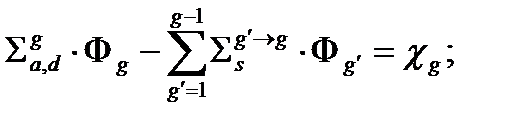(2.4.4)

Решение этой системы представляется в виде рекуррентного соотношения (2.4.5).

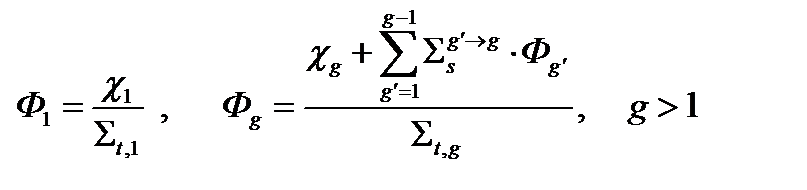(2.4.5)

После того, как мы определили групповые интегральные потоки 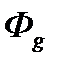, то есть групповой спектр нейтронов в размножающей среде, можно вычислить и коэффициент размножения этой среды 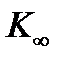в многогрупповом приближении (2.4.6), исходя из соотношения нормировки

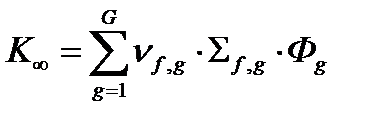. (2.4.6)

В общем случае, когда необходимо учитывать рассеяние нейтронов с приобретением энергии, система уравнений (2.4.2) решается численным методом, применяя ту же самую нормировку многогруппового спектра нейтронов.

Итак, для применения многогруппового приближения необходимо знать нуклидный состав размножающей среды и иметь систему многогрупповых констант для каждого нуклида, входящего в состав размножающей среды. Решая систему многогрупповых уравнений (2.4.2) тем или иным способом, получаем спектр нейтронов в многогрупповом приближении для данной размножающей среды. После этого, используя условие нормировки, определяем коэффициент размножения среды.

3. Реактор на тепловых нейтронах.

При дальнейшем увеличении разбавления ²³⁵U замедлителем, энергетический спектр нейтронов в среде будет все более смягчаться, так что часть замедляющихся нейтронов попадет по энергетической шкале в тепловую область, где их энергия сравнима с энергией теплового движения ядер среды. При достаточном количестве замедлителя в реакторе, значительная часть нейтронов деления смогут замедлиться до тепловых энергий. В таком реакторе основная доля делений будет осуществляться тепловыми нейтронами, это так называемый тепловой реактор. Следует отметить, что в тепловом реакторе присутствуют нейтроны всех энергий, быстрые, промежуточные и тепловые нейтроны.