СУЩЕСТВЕННАЯ И НЕСУЩЕСТВЕННАЯ АПРИОРНАЯ НЕОПРЕДЕЛЕННОСТЬ

Прежде чем перейти к обсуждению понятия оптимальности и кон­кретному рассмотрению методов решения задач синтеза в условиях априорной неопределенности и ограниченного статистического описания, основные типы которого были рассмотрены в гл. 3, полезно об­судить вопрос о том, какая же степень априорной неопределенности является существенной и действительно затрудняет решение задачи синтеза оптимальной системы по классическим байесовым приемам. Для того чтобы убедиться в том, что неполнота статистического описа­ния данных задачи не всегда ведет к невозможности нахождения оптимального правила принятия решения, рассмотрим сначала пример с довольно большой априорной неопределенностью.

Пусть требуется решить задачу различения сигналов (распознавания образов) по результатам наблюдения дискретной последовательности слу­чайных величин 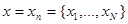, каждая компонента которой 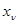является аддитивной смесью помехи 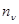и соответствующей компоненты одного из т возможных дискретных сигналов 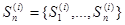. Ис­тинная ситуация заключается в том, что в реально наблюдаемой после­довательности 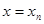может присутствовать любой из возможных сигна­лов 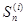, поэтому параметр , характеризующий ситуацию, просто нумеру­ет подлежащие различению сигналы и принимает значения ( ). 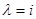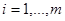Решение 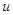заключается в том, чтобы по значениям наб­людаемой последовательности 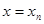вынести суждение, какой именно из сигналов 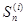присутствует в этой последовательности, то есть сводится к выбору одной из т альтернатив, 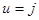( 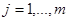). Будем считать, что априорные вероятности появления различных 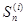одинаковы, то есть 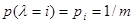, а последствия от любого неправильного решения также одинаковы (без ограничения общности потери от неправильного решения можно принять равными единице), правильное же решение дает нулевые потери. Последнее означает, что матрица потерь 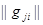имеет элементы

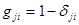, (4.2.1)

где 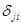- символ Кронекера.

Помеху 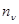будем считать гауссовой, некоррелированной, с нулевым математическим ожиданием. Априорная неопределенность будет свя­зана с часто имеющимся на практике незнанием интенсивности помехи, в результате чего дисперсия 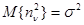неизвестна и является как раз одним из таких дополнительных неизвестных параметров функ­ции правдоподобия 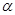, о которых шла речь в § 3.2. (В данном примере этот параметр одинаков для всех значений .)

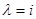Параметрически неопределенное описание функции правдоподобия 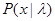будет иметь вид

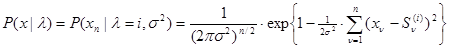. (4.2.2)

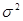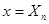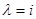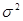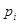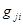Из-за наличия неизвестного параметра распределение вероятности данных наблюдения нам фактически неизвестно при любом значении , что, казалось бы, исключает возможность использования байесова подхода. Однако все-таки воспользуемся им, не обращая не­которое время внимания на то, что величина неизвестна. В соответ­ствии с общими правилами гл. 2 (2.4.6) и введенными предположения­ми о и апостериорный риск равен

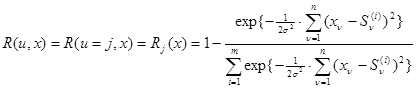. (4.2.3)

Это выражение зависит от интенсивности помехи 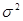и в связи с ее неопределенностью также является неопределенным. Тем не менее оптимальное правило решения может быть найдено точно, поскольку 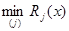независимо от значения 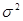достигается для того значения j, для которого величина

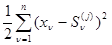(4.2.4)

минимальна или величина

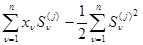(4.2.5)

максимальна.

Таким образом, оптимальное байесово правило решения имеет вид 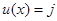, если

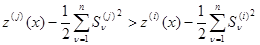(4.2.6)

для всех , ,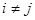

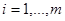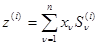(4.2.7)

и не зависит от неизвестного параметра 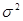, а следовательно, априорная неопределенность, связанная в данной задаче с незнанием интенсивно­сти помехи, является .несущественной.

Перейдем теперь к общему случаю. Пусть имеющаяся априорная неопределенность не позволяет задать плотности распределения веро­ятност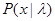и и 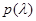и вместо них введены классы распределений вероятности P_l ( 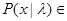P_l )и P₀( 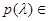P₀ ), такие, что любые из возможных при данной априорной неопределенност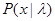и и 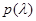принадлежат к этим .классам. В соответствии с материалами гл. 3 классы P_l и P₀могут быть произвольно широки, вплоть до множества всех неотрицательных нормируемых на единицу функций, как это про­исходит при полной априорной неопределенности. 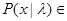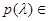Найдем апостериор­ный риск для какой-либо пары распределений х и , таких, что P_l , P₀ ,

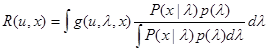. (4.2.8)

и попытаемся отыскать его минимум по решению .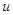

Если этот минимум достигается для значения 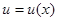, которое оди­наково для 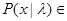P_l и 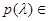P₀ , то очевидно, что априорная неопределенность статистического описания х и является несущест­венной. Само правило решения 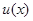, обладающее таким свойством, является равномерно наилучшим (по аналогии с терминологией, ис­пользуемой для двухальтернативных задач, оно может быть названо равномерно наиболее мощным правилом решения) для заданных клас­сов распределений вероятности P_l и P₀, поскольку оно обеспечивает абсолютную оптимальность при любой априорной неопределенности в пределах этих классов. Это правило обладает свойствами инвариант­ности, так как оно является одинаковым для любых распределений .данных наблюдений х и параметров , в пределах классов P_l и P₀, соответствующих имеющейся априорной неопределенности. Так, пра­вило решения (4.2.6) является равномерно наиболее мощным для клас­са задач различения сигналов, наблюдаемых на фоне гауссовых помех неизвестной интенсивности.

Конечно, существование подобных точных правил решений можно ожидать в довольно исключительных случаях, однако сам факт их на­личия делает целесообразным при решении задач синтеза в условиях априорной неопределенности прежде всего осуществить проверку существенности этой неопределенности стандартными байесовыми ме­тодами. Из (4.2.8) ясно, что априорная неопределенность заведомо является несущественной, если апостериорное распределение вероятно­стей имеет плотность

,

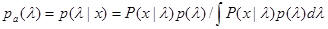одинаковую для всех 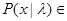P_l и 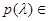P₀ . Можно найти и другие достаточно общие или, наоборот, конкретные условия, когда значение 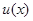, минимизирующее апостериорный риск, не зависит от априорной неопределенности.

Второе и, пожалуй, более важное обстоятельство заключается в том, что значительно чаще существуют приближенно равномерно наилучшие правила решения. Практически это имеет место в различного рода асим­птотических случаях - при большом объеме данных наблюдения х, ма­лой интенсивности помех, затрудняющих правильное принятие решения и т. п., одним словом, тогда, когда получающееся решение является «хо­рошим», то есть обладает высоким качеством и дает малый риск. Фактиче­ски решение задачи синтеза оптимальной системы в условиях априор­ной неопределенности так или иначе сводится к выявлению условий существования приближенного равномерно наилучшего решающего пра­вила и разработке конкретных методов его нахождения.