Равномерно наилучшее решение
Допустим, что для каждого фиксированного 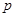 найден
найден 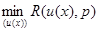 . Значение
. Значение 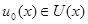 , при котором достигается этот минимум, то есть байесово правило решения, вообще говоря, зависит от
, при котором достигается этот минимум, то есть байесово правило решения, вообще говоря, зависит от 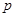 , так что при изменении
, так что при изменении 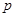 минимизирующее значение
минимизирующее значение 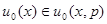 является функционалом
является функционалом 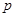 (рис. 4.1) и
(рис. 4.1) и
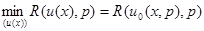 . (4.3.1)
. (4.3.1)
Если окажется, что минимум для всех 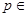 P достигается при одном и том же
P достигается при одном и том же 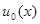 (рис. 4.2), то существует равномерно наилучшее решение, которое и является абсолютно оптимальным, а априорная неопределенность не является существенной. Само равномерно наилучшее решение может быть найдено с помощью обычной байесовой процедуры.
(рис. 4.2), то существует равномерно наилучшее решение, которое и является абсолютно оптимальным, а априорная неопределенность не является существенной. Само равномерно наилучшее решение может быть найдено с помощью обычной байесовой процедуры.
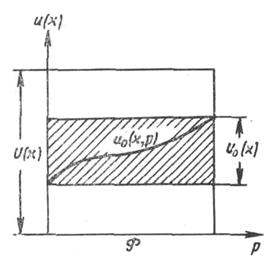
Рис. 4.1. Область оптимальных байесовых правил решений при различных 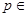 P
P
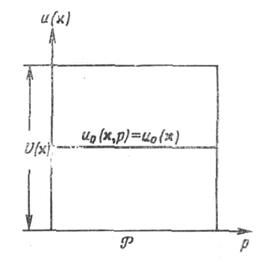
Рис. 4.2. Равномерно наилучшее правило решения
Следует отметить, что если ввести произвольную меру 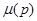 на множестве P (не обязательно имеющую вероятностный смысл) и проинтегрировать средний риск по этой мере, определив таким образом новый функционал решающего правила
на множестве P (не обязательно имеющую вероятностный смысл) и проинтегрировать средний риск по этой мере, определив таким образом новый функционал решающего правила
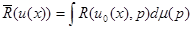 , (4.3.2)
, (4.3.2)
а затем найти значение 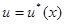 , минимизирующее этот функционал, то при существовании равномерно наилучшего решения это значение совпадает с
, минимизирующее этот функционал, то при существовании равномерно наилучшего решения это значение совпадает с 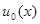 , то есть
, то есть 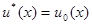 .
.
Это означает, что в случае существования равномерно наилучшего правила решения можно произвольно усреднять средний риск (в частности, при параметрической априорной неопределенности вводить для неизвестных параметров 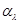 и
и 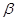 распределений вероятности х и
распределений вероятности х и  , в свою очередь, более или менее произвольные распределения вероятности) и искать минимум этого усредненного значения. Подобного рода усреднение во многих случаях может существенно упростить задачу в отношении техники отыскания оптимального правила решения благодаря большей простоте усредненного выражения.
, в свою очередь, более или менее произвольные распределения вероятности) и искать минимум этого усредненного значения. Подобного рода усреднение во многих случаях может существенно упростить задачу в отношении техники отыскания оптимального правила решения благодаря большей простоте усредненного выражения.
Дата добавления: 2018-05-10; просмотров: 1148;











