Минимаксиминный принцип (минимакс минимального среднего риска)

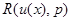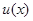Рассмотрим теперь общий случай, когда минимум риска по достигается при разных значениях 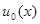для различных 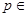P . Каждое из решений 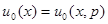является оптимальным байесовым решением для своего (неизвестного из-за наличия априорной неопреде­ленности) значения 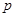, а их совокупность образует некоторое подмноже­ство 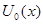байесовых решающих правил (на рис. 4.1. заштрихованный прямоугольник). При этом если мы возьмем какое-то из этих правил 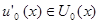, то оно обязательно соответствует некоторому 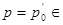P, обеспечивая минимум апостериорного и среднего риска для этого 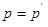и в то же время для других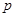

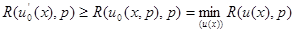при .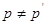

Предположим, что мы хотим ограничить свой выбор только множе­ством 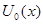, то есть выбирать правила решения среди оптимальных байе­совых для всевозможных, но каждый раз известных 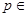P. Фактически это означает устранение априорной неопределенности выбором какого-то заранее определенного значения 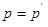и синтезом системы для вполне определенных условий, соответствующих этому значению. Возникает вопрос, как выбрать значение 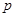(и соответствующее ему решение 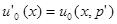). Естественный способ заключается в применении прин­ципа минимакса к величине байесова риска. При этом значение 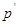вы­бирается из условия

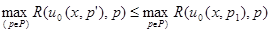для всех 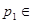P. (4.3.5)

где 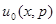- оптимальное байесово правило решения, выбираемое из условия 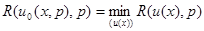при данном 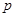. Процедура выбора правила решения, удовлетворяющая рассматриваемому принципу, эквивалентна выбору 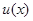, обеспечивающего

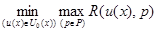. (4.3.6)

Рассматриваемый принцип достаточно прост, так как не требует разработки существенно новой методики выбора правила решения. Он целиком основывается на технике получения байесовых правил решения, поскольку ограничивает выбор только такими правилами для различ­ных 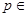P и, конечно, автоматически приводит к равномерно наилучше­му правилу решения, если оно существует. В то же время ясно, что именно указанное ограничение (выбор 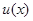только из подмножества 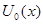) не гарантирует от того, что будет упущено какое-то лучшее в условиях априорной неопределенности правило решения. Подмножество 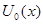, вообще говоря, не тождественно полному классу решающих правил, о котором шла речь в гл. 2, поскольку оно соответствует «услов­но» байесовым решениям, каждое из которых получается в предположе­нии о полностью известной статистике. Полный класс решающих пра­вил для рассматриваемой задачи с априорной неопределенностью полу­чается, если взять множество всех 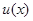, минимизирующих усредненный риск 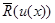из (4.3.2) для всевозможных нормированных на единицу мер 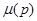, которые трактуются при этом как некоторые априорные рас­пределения на множестве P , описывающем априорную неопределен­ность.

Минимаксиминный принцип слабо использует или вообще игнори­рует ту избыточность в данных наблюдения, которая может являться компенсацией за априорную неопределенность. (В примере п. 4.3.2 минимаксиминное правило будет иметь вид (4.3.4) при некотором 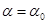и не будет учитывать наличие наблюдений { 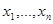}.) В то же время до­вольно легко оценить степень приближения решения, полученного на основе этого принципа, к абсолютно оптимальному (при отсутствии априорной неопределенности). Критерием близости может служить раз­ность

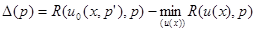. (4.3.7)

Если при всех значениях 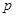эта разность не превышает допустимо ма­лой величины 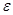(вообще говоря, зависящей от 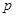), то правило решения 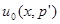является приближенным равномерно наилучшим правилом с уровнем приближения, не худшим чем 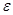. Таким образом, использование рассматриваемого принципа дает возможность выявить, существует или нет приближенное равномерно наилучшее правило решения, и получить его с помощью стандартной байесовой процедуры. Вообще говоря, ясно, что разность 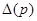из (4.3.7) может оказаться достаточно малой только в том случае, когда множество P содержит не слишком много элемен­тов, отличающихся от некоторого истинного, но неизвестного значения 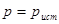. В противном случае, если, например, множество P неограниче­но, средний риск минимаксиминного правила решения может достигать величины максимального значения функции потерь, а при неограничен­ной функции потерь может также стать неограниченным. Таким обра­зом, минимаксиминный принцип предпочтения действительно серьезно препятствует выбору плохих правил решения только тогда, когда апри­орная неопределенность относительно невелика. В общем же случае он позволяет выбирать и непригодные правила решения, поэтому ценность этого принципа предпочтения невелика.