ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

Неполнота статистического описания задачи, типичная для прак­тики синтеза информационных систем самого различного назначения, требует особых подходов при нахождении оптимальных правил приня­тия решения - алгоритмов обработки информации в синтезируемых системах. Эти подходы должны в какой-то степени отличаться от чисто байесова подхода к решению задач синтеза, который, обладая наиболь­шим совершенством в смысле обеспечения качества синтезируемой си­стемы, требует достаточно полного статистического описания всех данных, имеющих значение для рассматриваемой задачи.

В этой и последующих главах мы рассмотрим различные подходы к решению задачи синтеза информационных систем в условиях априор­ной неопределенности и соответствующие им методы нахождения пра­вил принятия решения. Безусловно, это рассмотрение не будет исчерпывающим, поскольку область науки, связанная с нахождением правил принятия решения в условиях априорной неопределенности, развивается очень бурно, особенно в последние годы. Конкретные пред­ложения и идеи столь многообразны, что, по-видимому, достаточно трудно даже провести их четкую классификацию, не говоря уже о под­робном их изложении. Основное внимание необходимо уделить тем подходам, которые по возможности в максимальной степени используют ограниченные априорные сведения и для различных ситуа­ций неполного статистического описания (гл. 3) дают оптимальные или практически оптимальные правила принятия решений. Другое основное требование - конструктивный характер подхода, то есть обеспечение воз­можности практического решения достаточно широкого круга конкрет­ных задач с доведением этого решения до ясно интерпретируемых результатов, которые могли бы быть реализованы соответствующими вычислительными процедурами, схемами устройств и т. д. Выполнение этих требований приводит иногда к целесообразности сочетания раз­личных подходов, что в еще большей степени подчеркивает необходи­мость понимания и овладения ими для решения практических задач синтеза правил принятия решения и соответствующих им информаци­онных систем.

Если теперь перейти к формальному описанию задачи, то основная ее особенность заключается в том, что из-за имеющейся априорной неопределенности статистического описания данных наблюдения х и параметров , влияющих на последствия решения, невозможно однозначно определить распределения вероятности х и , и, следовательно, величину среднего риска, который является критерием качества для любого возможного правила решения.

При наличии априорной неопределенности лучшее, что можно сде­лать для статистического описания х и - это задать некоторые множества P_lфункций правдоподобия 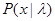и P₀априорных плотно­стей вероятности 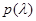. Способ задания P_lи P₀,, их структура и полнота определяются имеющимися ограниченными сведениями и могут соответствовать любому из рассмотренных в гл. 3 случаев (ограничен­ным числом статистических характеристик, параметрически, с помощью эмпирических данных и т. д.).

Так как каждой паре 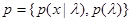при любом решении и согласно основному определению (2.3.3) соответствует свое значение среднего риска, последний является функционалом не только правила решения 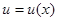, но и этой пары плотностей вероятности 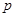, то есть

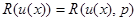, (4.1.1)

и, следовательно, может принимать при данном объеме ограниченных априорных сведений любое значение, соответствующее значению 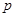из множества допустимых значения P = {P_l , P₀,}, описывающего совокупность всех возможных при имеющейся в данной задаче априорной неопределенности функци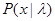й и 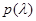. (В байесовой задаче 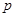имеет вполне определенное значение, поэтому зависимость среднего риска от 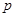обычно не подчеркивается..)

Задачей синтеза в условиях априорной неопределенности является отыскание такого правила решения 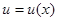(или вообще говоря, реша­ющей функции 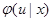), которое в соответствии с установленным по­рядком обеспечивало бы именно этому решению наиболее высокую степень предпочтения при всех возможных 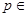P. Сам порядок пред­почтения, устанавливающий понятие об оптимальности решения, оче­видно, из-за неопределенности величины среднего риска уже не всегда может быть таким простым, как в байесовой задаче, где считается более предпочтительным то правило решения 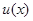, для которого сред­ний риск меньше, а оптимальным то, для которого он минимален.