ЭМПИРИЧЕСКИЙ ПОДХОД В ЗАДАЧАХ С АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТЬЮ.

ОБУЧЕНИЕ

Рассмотренные выше аналитические способы неполного статистиче­ского описания х и по существу соответствуют тому, что в каждой конкретной практической задаче создается некоторая аналитическая мо­дель для описания статистических свойств х и с той степенью полноты и подробности, которая соответствует имеющимся знаниям о закономер­ностях их поведения, физических свойствах, взаимосвязи между собой. Подобная модель является в какой-то степени наиболее сжатым опи­санием имеющегося прошлого опыта, содержащего как результаты изу­чения указанных закономерностей, так и, возможно, эмпирические дан­ные относительно х и .

На практике бывает и так, что, кроме эмпирических данных, всякая иная априорная информация относительно х и отсутствует. Однако если эти данные получены в обстановке, статистически однородной или хотя бы статистически связанной с той, в которой принимается решение no данным наблюдения х, то они являются в определенной степени статистическим эквивалентом аналитических моделей для распределе­ний вероятности х и , необходимых для нахождения оптимального правила принятия решения. Степень этой эквивалентности, естественно, зависит от объема имеющихся эмпирических данных, которые, в свою очередь, могут быть использованы по-разному: непосредственно для нахождения недостающих распределений вероятности, для оценки функциональной зависимости апостериорного риска от х и решения u, для уточнения структуры и параметров решающего правила (алгорит­ма обработки данных наблюдения х). Процедуру использования эмпи­рических данных, которые характеризуют прошлый опыт, обычно на­зывают обучением, а соответствующие алгоритмы — обучаемыми.

Для того чтобы яснее представить себе возможный качественный состав имеющихся эмпирических данных и возможные способы их ис­пользования при синтезе систем в условиях априорной неопределенности, предположим, что имеется серия повторяющихся ситуаций, статистически однородных или хотя бы статически связанных с той, в которой мы должны принимать решение. Последняя (в соответствии с гл. 2) характеризуется значением параметра , определяющего вели­чину потерь 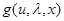при принятии решения u, и данными наблюде­ния х, на основе которых принимается решение в соответствии с пра­вилом u = u(x). Пусть теперь имеется N ситуаций, сходных или связан­ных с основной, в которых получены те или иные эмпирические данные. Каждая из них для 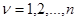характеризуется значением пара­метров 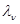, имеющих ту же природу, состав и содержание, что и параметры . Иными словами, если для ситуации, в которой принимается интересующее нас решени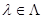е, , где 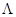- множество возможных зна­чений параметров , то и каждое из значений 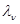является одним из возможных элементов множества 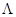; если имеет распределение с плотностью 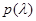, то и каждое из значений 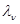имеет то же распределение.

В общем случае эмпирические данные представляют собой совокуп­ность значений 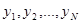, каждая из составляющих 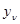этой совокупности соответствует значению 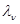и может содержать тот или иной объем сведений. Характер, значимость и способы использования этих све­дений существенно различаются в зависимости от того, производится ли в 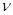-й ситуации только наблюдение и регистрация каких-либо данных (аналогичных х для основной рабочей ситуации либо как-то отличаю­щихся от х) или наряду с наблюдением, так же как в рабочей ситуации, осуществляется принятие решения 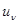с вытекающими отсюда последствиями. Согласно принятой терминологии, в первом случае гово­рят о простом обучении, а во втором - о «рабочеподобном». Смысл последнего термина связан с тем, что при получении эмпирических данных воспроизводится не только ситуация, характеризуемая значе­нием параметра 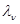, определяющим потери, но и сам процесс решения, подобный тому, который должен быть выполнен в рабочей ситуации. Это является принципиальной основой для получения информации о конкретной величине потерь от принятия решения на каждом 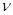-м ша­ге и использования этой информации для улучшения правила принятия решения на рабочем шаге.

Рассмотрим более полно возможный состав эмпирических дан­ных - совокупности 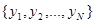для различных случаев. Заметим, что эта совокупность часто называется обучающей последовательностью.

Простое обучение

1. Самый простой случай эмпирической статистики - это случай, когда в серии из N независимых наблюдений получены значения 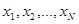, где каждая из составляющих 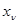тождественна с точки зрения объема и содержания наблюдаемых данных величине х, получаемой в рабочей ситуации, а значени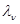я для 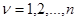известны. В этом случае любая из составляющих 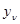совокупности эмпирических дан­ных представляет собой пару 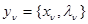, где 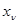под­чиняется тому же условному распределению вероятности (полностью или частично неизвестному), что и х. Совместное условное распределе­ние вероятности для совокупности значений 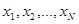иданных наблю­дения х в рабочей ситуации может быть описано плотностью вероят­ности

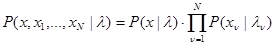, (3.3.1)

где 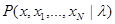- всюду одна и та же функция; 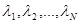известны,
а , определяющая величину потерь в рабочей ситуации, неизвестна. В частном случае дискретного множества значений ( 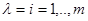) последовательность 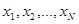иногда удобно разбить на последователь­ности 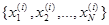( 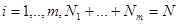), соответству­ющие имеющимся эмпирическим данным для каждого из значений 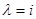. Заметим, что случай, когда на каждом 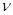-м шаге в процессе эмпириче­ского набора данных наряду с результатом наблюдения 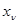становится известным и истинное состояние ситуации, характеризуемое параметра­ми 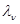, называется иногда обучением с учителем.

2. Следующий характерный случай, когда каждая из составляющих 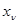эмпирической совокупности по-прежнему тождественна по объему и содержанию величине х, но значения параметров 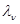неизвестны, то есть истинная ситуация, в которой наблюдается 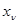, остается неизвестной. 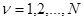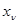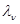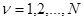При этом также предполагается, что все ситуации для , в ко­торых получены эмпирические данные и рабочая ситуация статистичес­ки однородны, то есть все для и имеют одно и то же распределение вероятности. Совместное распределение вероятности { 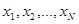}и х при заданном значении , для рабочей ситуации в этом случае мо­жет быть описано следующей плотностью:

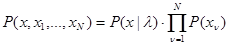, (3.3.2)

где 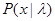- функция правдоподобия (полностью либо частично неиз­вестная), а

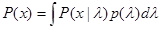, (3.3.3)

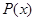- плотность безусловного распределения вероятности х, неопределен­ность которой может быть еще большей, чем функции правдоподобия, из-за частичного либо полного незнания априорного распределения
параметров (плотности ).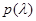

3. Более общий случай имеет место, если в процессе набора эмпи­рических данных наблюдаются величины 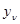не обязательно тождественные по объему и содержанию х и , но связанные с ними известной функциональной либо более общей вероятностной зависимостью. Это означает, что любая из составляющих 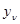может быть описана услов­ным распределением вероятности с плотностью 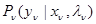, которое может быть полностью или частично неизвестным (при наличии функ­циональной зависимости указанная плотность дельтообразна), а пол­ная совокупность эмпирических данных { 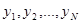} и данных наблю­дения х в рабочей ситуации имеет условное (при заданном ) распределение с плотностью вероятности

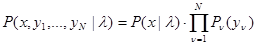, (3.3.4)

где

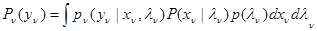. (3.3.5)

Величины 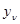могут представлять собой, например, отдельные компоненты полного вектора данных наблюдения х (не обязательно одинаковые при разных 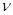), результат наблюдения 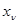с дополнительными помехами и ошибками или, наоборот, в лучших по сравнению с рабочей ситуацией условиях и т. п.

Следует отметить, что независимость отдельных составляющих совокупности эмпирических данных, которая использована при записи (3.3.1), (3.3.2), (3.3.4), не имеет принципиального значения. Важно лишь существование той или иной степени статистического подобия между рабочей ситуацией и ситуациями, в которых получены эмпири­ческие данные, а распространение рассуждений на случай зависимости 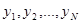и х сводится лишь к соответствующему изменению формы записи совместных распределений вероятности.

На основании проведенного выше рассмотрения можно зафиксиро­вать несколько существенных моментов.

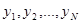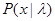а). Совокупность эмпирических данных { } имеет ценность с точки зрения принятия решения в рабочей ситуации только в том слу­чае, если имеется априорная неопределенность относительно статистиче­ского описания х и . Действительно, если и 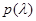известны, то,,
как следует из выражений для среднего и апостериорного риска гл. 2 и выражений (3.3.1), (3.3.2), (3.3.4), расширение полной совокупности данных наблюдения за счет использования эмпирических данных
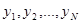( }, то есть увеличение входной информации с заменой х на сово­купность { 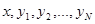}, не изменяет ни оптимального правила реше­ния и (оно остается зависящим только от х), ни величины
соответствующего ему риска. Это совершенно естественно, поскольку данные прошлых наблюдений { 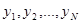} не содержат непосредственно сведений о значении ненаблюдаемых параметров , определяющих ве­личину потерь от принятия того или иного решения. Если неопределен­ность относится только к априорному распределению вероятности ( 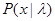известно), не имеют ценности эмпирические данные 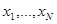при обучении с учителем (в этом случае полезны только значения { 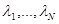}, несущие информацию о структуре ).

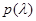Сформулированные выводы в равной степени относятся как к простому обучению, так и к «рабочеподобному»

б).Для описания частично или полностью неизвестных распределе­ний вероятности совокупности х и эмпирических данных 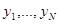могут быть использованы все обсуждавшиеся в § 3.1, 3.2 методы и, в частности, с успехом применены рассмотренные в § 3.2 методы пара­метрического описания в случае ограниченных априорных значений. При этом эмпирические данные являются источником информации о неизвестных значениях параметров 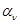и 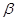функции правдоподобия и априорного распределения вероятности .

в). Наличие эмпирических данных 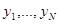, полученных простым .наблюдением без принятия решения в каждой 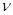-й ситуации (простое обучение), нисколько не изменяет исходную постановку задачи стати­стического решения и ее общую формулировку как в байесовом случае, так и при наличии априорной неопределенности. Действительно, так как потери зависят только от значения параметров , в рабочей ситуации (и не зависят от 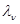, 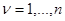), назовем совокупностью данных наблюдения х и то, что мы раньше обозначали этой буквой и вместе с ним все остальные имеющиеся данные, полученные в процессе эмпи­рического изучения статистики, то есть произведем переобозначение 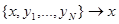. Поскольку конкретное содержание совокупности х не было ограничено, то естественно, что от такого переобозначения ничего не изменится. Поэтому специальное выделение совокупности данных { 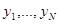}, отражающих прошлый опыт, имеет весьма ограни­ченное значение, а терминология, связанная с понятием обучения, мо­жет быть удобна только из-за наглядности рассуждений.

Забегая вперед, необходимо отметить, что этот вывод справедлив и для «рабочеподобного» обучения, если потери во всех ситуациях ( 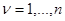), за исключением рабочей, равны нулю или несущественны.