Неопределенность, количество информации и энтропия
Основоположенник теории информации Клод Шеннон определил информацию, как снятую неопределенность. Точнее сказать, получение информации - необходимое условие для снятия неопределенности. Неопределенность возникает в ситуации выбора. Задача, которая решается в ходе снятия неопределенности – уменьшение количества рассматриваемых вариантов (уменьшение разнообразия), и в итоге выбор одного соответствующего ситуации варианта из числа возможных. Снятие неопределенности дает возможность принимать обоснованные решения и действовать. В этом управляющая роль информации.
Представьте, что вы зашли в магазин и попросили продать вам жевательную резинку. Продавщица, у которой, скажем, 16 сортов жевательной резинки, находится в состоянии неопределенности. Она не может выполнить вашу просьбу без получения дополнительной информации. Если вы уточнили, скажем, - «Orbit», и из 16 первоначальных вариантов продавщица рассматривает теперь только 8, вы уменьшили ее неопределенность в два раза (забегая вперед, скажем, что уменьшение неопределенности вдвое соответствует получению 1 бита информации). Если вы, не мудрствуя лукаво, просто указали пальцем на витрине, - «вот эту!», то неопределенность была снята полностью. Опять же, забегая вперед, скажем, что этим жестом в данном примере вы сообщили продавщице 4 бита информации.
Ситуация максимальной неопределенности предполагает наличие нескольких равновероятных альтернатив (вариантов), т.е. ни один из вариантов не является более предпочтительным. Причем, чем больше равновероятных вариантов наблюдается, тем больше неопределенность, тем сложнее сделать однозначный выбор и тем больше информации требуется для этого получить. Для N вариантов эта ситуация описывается следующим распределением вероятностей: {1/N, 1/N, … 1/N}.
Минимальная неопределенность равна 0, т.е. эта ситуация полной определенности, означающая что выбор сделан, и вся необходимая информация получена. Распределение вероятностей для ситуации полной определенности выглядит так: {1, 0, …0}.
Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия, точнее информационная энтропия.
Энтропия (H) – мера неопределенности, выраженная в битах. Так же энтропию можно рассматривать как меру равномерности распределения случайной величины.
|
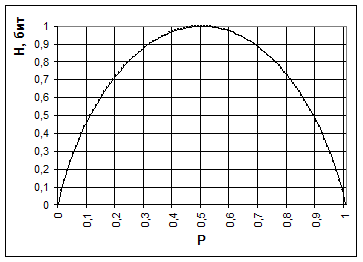
| Рис. 8. Поведение энтропии для случая двух альтернатив. |
На рисунке 8. показано поведение энтропии для случая двух альтернатив, при изменении соотношения их вероятностей (p, (1-p)).
Максимального значения энтропия достигает в данном случае тогда, когда обе вероятности равны между собой и равны ½, нулевое значение энтропии соответствует случаям (p0=0, p1=1) и (p0=1, p1=0).
Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. По определению Леона Бриллюэна информация есть отрицательная энтропия (негэнтропия).
|
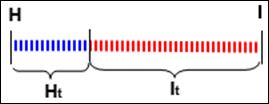
| Рис. 9. Связь между энтропией и количеством информации. |
Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.
При частичном снятии неопределенности, полученное количество информации и оставшаяся неснятой неопределенность составляют в сумме исходную неопределенность. Ht + It = H.
По этой причине, формулы, которые будут представлены ниже для расчета энтропии H являются и формулами для расчета количества информации I, т.е. когда речь идет о полном снятии неопределенности, H в них может заменяться на I.
Формула Шеннона
В общем случае, энтропия H и количество получаемой в результате снятия неопределенности информации I зависят от исходного количества рассматриваемых вариантов N и априорных вероятностей реализации каждого из них P: {p0, p1, …pN-1}, т.е. H=F(N, P). Расчет энтропии в этом случае производится по формуле Шеннона, предложенной им в 1948 году в статье "Математическая теория связи".
В частном случае, когда все варианты равновероятны, остается зависимость только от количества рассматриваемых вариантов, т.е. H=F(N). В этом случае формула Шеннона значительно упрощается и совпадает с формулой Хартли, которая впервые была предложена американским инженером Ральфом Хартли в 1928 году, т.е. не 20 лет раньше.
Формула Шеннона имеет следующий вид:
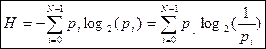 (1)
(1)
Знак минус в формуле (1) не означает, что энтропия – отрицательная величина. Объясняется это тем, что pi£1 по определению, а логарифм числа меньшего единицы - величина отрицательная. По свойству логарифма 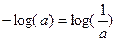 , поэтому эту формулу можно записать и во втором варианте, без минуса перед знаком суммы.
, поэтому эту формулу можно записать и во втором варианте, без минуса перед знаком суммы.
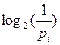 интерпретируется как частное количество информации
интерпретируется как частное количество информации 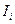 , получаемое в случае реализации i-ого варианта. Энтропия в формуле Шеннона является средней характеристикой – математическим ожиданием распределения случайной величины {I0, I1, … IN-1}.
, получаемое в случае реализации i-ого варианта. Энтропия в формуле Шеннона является средней характеристикой – математическим ожиданием распределения случайной величины {I0, I1, … IN-1}.
Приведем пример расчета энтропии по формуле Шеннона. Пусть в некотором учреждении состав работников распределяется так: ¾ - женщины, ¼ - мужчины. Тогда неопределенность, например, относительно того, кого вы встретите первым, зайдя в учреждение, будет рассчитана рядом действий, показанных в таблице 1.
Таблица 1.
| pi | 1/pi | Ii=log2(1/pi), бит | pi*log2(1/pi), бит | |
| Ж | 3/4 | 4/3 | log2(4/3)=0,42 | 3/4 * 0,42=0,31 |
| М | 1/4 | 4/1 | log2(4)=2 | 1/4 * 2=0,5 |
| å | 1 | H=0,81 бит |
Если же априори известно, что мужчин и женщин в учреждении поровну (два равновероятных варианта), то при расчете по той же формуле мы должны получить неопределенность в 1 бит. Проверка этого предположения проведена в таблице 2.
Таблица 2.
| pi | 1/pi | Ii=log2(1/pi), бит | pi*log2(1/pi), бит | |
| Ж | 1/2 | log2(2)=1 | 1/2 * 1=1/2 | |
| М | 1/2 | log2(2)=1 | 1/2 * 1=1/2 | |
| å | 1 | H=1 бит |
Формула Шеннона (1) совпала по форме с формулой Больцмана, полученной на 70 лет ранее для измерения термодинамической энтропии идеального газа. Эта связь между количеством информации и термодинамической энтропией послужила сначала причиной горячих дискуссий, а затем – ключом к решению ряда научных проблем. В самом общем случае энтропия понимается как мера неупорядоченности, неорганизованности материальных систем.
В соответствии со вторым законом термодинамики закрытые системы, т.е. системы лишенные возможности вещественно-энергетически-информационного обмена с внешней средой, стремятся, и с течением времени неизбежно приходят к естественному устойчивому равновесному внутреннему состоянию, что соответствует состоянию с максимальной энтропией. Закрытая система стремится к однородности своих элементов и к равномерности распределения энергии связей между ними. Т.е. в отсутствии информационного процесса материя самопроизвольно забывает накопленную информацию.
Формула Хартли
Мы уже упоминали, что формула Хартли – частный случай формулы Шеннона для равновероятных альтернатив.
Подставив в формулу (1) вместо pi его (в равновероятном случае не зависящее от i)значение 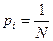 , получим:
, получим:
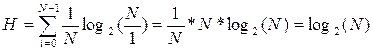 , таким образом, формула Хартли выглядит очень просто:
, таким образом, формула Хартли выглядит очень просто:
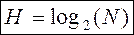 (2)
(2)
Из нее явно следует, что чем больше количество альтернатив (N), тем больше неопределенность (H). Эти величины связаны в формуле (2) не линейно, а через двоичный логарифм. Логарифмирование по основанию 2 и приводит количество вариантов к единицам измерения информации – битам.
Заметьте, что энтропия будет являться целым числом лишь в том случае, если N является степенью числа 2, т.е. если N принадлежит ряду: {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048…}
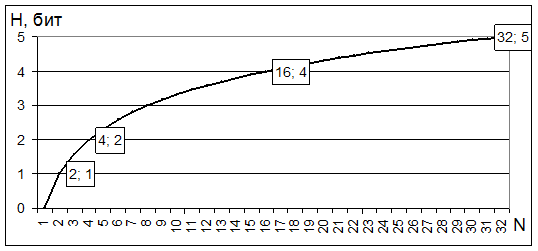
Рис. 10. Зависимось энтропии от количества равновероятных вариантов выбора (равнозначных альтернатив).
Напомним, что такое логарифм.
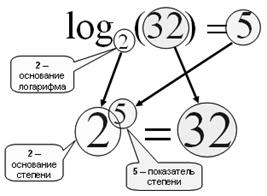
Рис. 11. Нахождение логарифма b по основанию a - это нахождение степени, в которую нужно возвести a, чтобы получить b.
Логарифм по основанию 2 называется двоичным:
log2(8)=3 => 23=8
log2(10)=3,32 => 23,32=10
Логарифм по основанию 10 –называется десятичным:
log10(100)=2 => 102=100
Основные свойства логарифма:
1. log(1)=0, т.к. любое число в нулевой степени дает 1;
2. log(ab)=b*log(a);
3. log(a*b)=log(a)+log(b);
4. log(a/b)=log(a)-log(b);
5. log(1/b)=0-log(b)=-log(b).
Для решения обратных задач, когда известна неопределенность (H) или полученное в результате ее снятия количество информации (I) и нужно определить какое количество равновероятных альтернатив соответствует возникновению этой неопределенности, используют обратную формулу Хартли, которая выглядит еще проще:
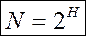 (3)
(3)
Например, если известно, что в результате определения того, что интересующий нас Коля Иванов живет на втором этаже, было получено 3 бита информации, то количество этажей в доме можно определить по формуле (3), как N=23=8 этажей.
Если же вопрос стоит так: “в доме 8 этажей, какое количество информации мы получили, узнав, что интересующий нас Коля Иванов живет на втором этаже?”, нужно воспользоваться формулой (2): I=log2(8)=3 бита.
Дата добавления: 2016-11-26; просмотров: 2324;











