Сложное движение точки
Если материальная точка участвует сразу в двух движениях, то такое движение называется сложным. Движение точки относительно подвижной системы отсчета называется относительным, и его кинематические характеристики имеют верхний индекс «r». Движение же точки вместе с подвижной системой отсчета называется – переносным (имеет индекс «е»). Суммарное или результирующее движение точки относительно неподвижной системы отсчета (часто она связана с землей) называется – абсолютным (индекс «а»).
В этом случае для кинематических характеристик справедливы следующие зависимости
 , (5)
, (5)
где 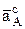 – кориолисово ускорение, возникающее из-за взаимодействия переносного и относительного движений.
– кориолисово ускорение, возникающее из-за взаимодействия переносного и относительного движений.
Оно определяется по правилам векторного произведения, т.к. 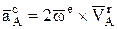 . Вектор результат
. Вектор результат 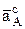 перпендикулярен плоскости, в которой лежат вектора сомножители и направлен по правилу правого винта, если первый вектор
перпендикулярен плоскости, в которой лежат вектора сомножители и направлен по правилу правого винта, если первый вектор 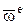 кратчайшим путем совмещать со вторым
кратчайшим путем совмещать со вторым 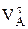 . При этом вектор
. При этом вектор 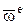 – угловой скорости переносного движения всегда лежит на оси переносного вращения (в любой точке) и направлен согласно правилу правого винта, примененному к известному направлению вращ
– угловой скорости переносного движения всегда лежит на оси переносного вращения (в любой точке) и направлен согласно правилу правого винта, примененному к известному направлению вращ 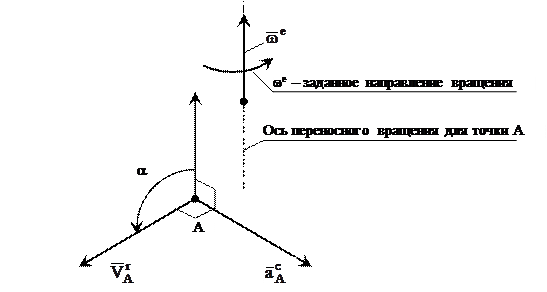 ения (рис. 3).
ения (рис. 3).

Рис. 3
По модулю 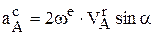 , и оно может быть равно нулю в двух случаях: если
, и оно может быть равно нулю в двух случаях: если 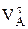 параллельно
параллельно 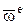 , т.е. a=0, и если переносное движение не связано с поворотом подвижной системы отсчета (её оси перемещаются параллельно самим себе, т.е. поступательно и
, т.е. a=0, и если переносное движение не связано с поворотом подвижной системы отсчета (её оси перемещаются параллельно самим себе, т.е. поступательно и  ).
).
Если переносное или относительное движение точки являются криволинейными, то в выражениях (5) удобно соответствующее ускорение разложить на два вектора: касательного и нормального ускорения, например 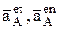 .
.
Уравнения (5) могут быть решены двумя очень распространенными в кинематике способами: графическим или аналитическим, при условии, если в них содержится только две неизвестные. При этом под неизвестными отдельно понимаются модуль (величина) или направление какого-то из векторов. Чаще всего при решении задач можно встретить два случая. Первый, когда из (5) необходимо найти величину и направление одного вектора 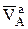 или
или 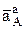 , а для остальных векторов величины и направления (углы с одной из осей Х или Y) заданы или легко находятся по исходным данным задачи. Второй случай, когда все вектора в одном из выражений (5) известны по направлению, а надо найти величины двух из них, например
, а для остальных векторов величины и направления (углы с одной из осей Х или Y) заданы или легко находятся по исходным данным задачи. Второй случай, когда все вектора в одном из выражений (5) известны по направлению, а надо найти величины двух из них, например 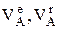 .
.
Графический способ предполагает рисование векторов, входящих в (5) с использованием заранее выбранного масштаба. Тогда при сложении векторов конец первого является началом второго  вектора или через него проводят прямую, если известно только направление второго вектора. Результирующий вектор
вектора или через него проводят прямую, если известно только направление второго вектора. Результирующий вектор 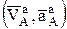 проводят из начала первого к концу последнего из складываемых векторов. В результате графического решения получается замкнутый многоугольник (треугольник), в котором искомые по величине вектора измеряют и умножают на выбранный масштаб для определения их величины (рис. 4).
проводят из начала первого к концу последнего из складываемых векторов. В результате графического решения получается замкнутый многоугольник (треугольник), в котором искомые по величине вектора измеряют и умножают на выбранный масштаб для определения их величины (рис. 4).
Рассмотрим пример, в котором известные величины или направления векторов обозначим внизу штрихом, а неизвестные знаком вопроса
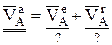 направления
направления
величины векторов
Однако наиболее часто применяется второй аналитический способ решения уравнений (5), когда их проецируют почленно на выбранные оси X и Y, а затем решают полученную систему двух алгебраических уравнений с двумя неизвестными. В рассмотренном выше примере, когда вектор 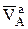 задан по величине и направлению (ось X выбрана по направлению
задан по величине и направлению (ось X выбрана по направлению 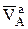 ), а вектора
), а вектора 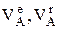 известны только по направлениям, заданными углами с осью X проецирование векторного уравнения на оси дает следующий результат:
известны только по направлениям, заданными углами с осью X проецирование векторного уравнения на оси дает следующий результат:
для оси Х: 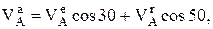
для оси Y: 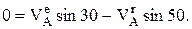
Решение последней системы уравнений позволяет определить величины векторов 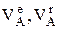 (
(  должно быть известно или определено по исходным данным, например путем дифференцирования уравнений движения, как показано в (2) и (3)).
должно быть известно или определено по исходным данным, например путем дифференцирования уравнений движения, как показано в (2) и (3)).
Рассмотрим две конкретные задачи с использованием уравнений (5) для сложного движения точки.
Задача 1
Здесь рычаг манипулятора поворачивается в горизонтальной плоскости и одновременно вдоль рычага перемещается ползун с захватом (материальная точка А) (рис. 5).
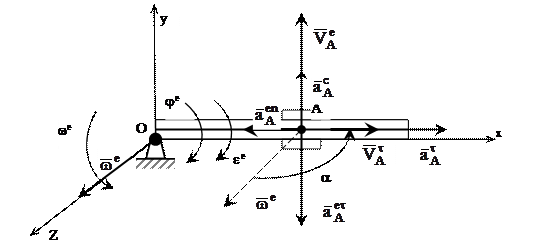

Рис. 5
Дано: 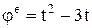 (рад.),
(рад.), 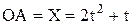 (м).
(м).
Найти: 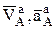 при t=1 c.
при t=1 c.
Решение: Движение точки А является сложным: относительное движение вдоль рычага и переносное, т.е. поворот вместе с рычагом.
Сначала определим положение точки А в её относительном движении при
t=1 c и найдем в этом положении  по величине и направлению.
по величине и направлению.
Для относительного движения
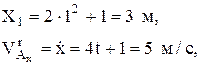
т.к. движение по прямой вдоль оси Х, то  и
и 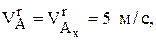 аналогично
аналогично 
Для переносного движения:
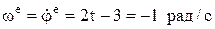 – угловая скорость переносного движения;
– угловая скорость переносного движения;
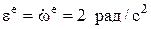 – его угловое ускорение (знак « - » у we , полученный после дифференцирования и подстановки значения t означает, что направление вращения против положительного отсчета координаты j, принятого в задаче, а знак « + » у ee означает, что направление ускорения совпадает с j);
– его угловое ускорение (знак « - » у we , полученный после дифференцирования и подстановки значения t означает, что направление вращения против положительного отсчета координаты j, принятого в задаче, а знак « + » у ee означает, что направление ускорения совпадает с j);
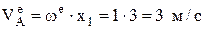 – вращательная скорость перпендикулярна радиусу ОА и направлена в сторону we;
– вращательная скорость перпендикулярна радиусу ОА и направлена в сторону we;
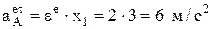 – перпендикулярна радиусу в сторону ee;
– перпендикулярна радиусу в сторону ee;
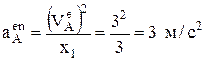 – по радиусу к центру О.
– по радиусу к центру О.
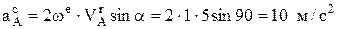 .
.
Итак 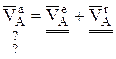 , т.к.
, т.к. 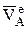 перпендикулярно
перпендикулярно 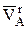 , то последнее уравнение можно не проецировать на оси Х и Y, а использовать теорему Пифагора
, то последнее уравнение можно не проецировать на оси Х и Y, а использовать теорему Пифагора
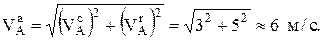
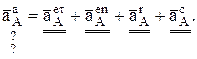
После проецирования на оси Х и Y получим

Задача 2
Рассмотрим случай, когда абсолютные кинематические характеристики движения рассматриваемой точки легко находятся, а с помощью уравнений (5) определяются характеристики переносного и относительного движения в определенном заданном положении механизма (рис. 6).
Дано: V1 =0,2 м/с, а1 =0,1 м/с2, j=60°, Н=0,5 м.
Найти: w3, e3.
Решение: Механизм состоит из трех звеньев: звено 1 – шток гидроцилиндра (ведущее); звено 2 – ползун (промежуточное), которое скользит вдоль звена 3 – кулиса (ведомое). Тем самым поступательное движение звена 1 преобразовывается в поворотное звена 3.
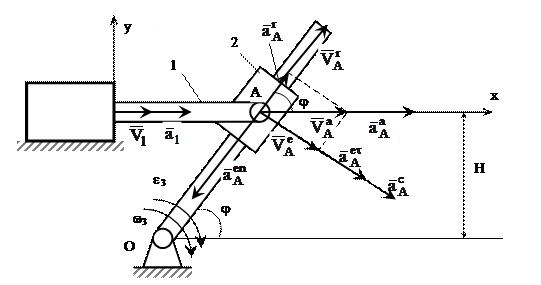

Рис. 6
При решении применяется распространенный прием кинематики: переход от одного звена к другому через их общую точку (здесь точка А). При этом учитывается, что кинематические характеристики этой точки одинаковы, но они определяются сначала по формулам и правилам движения первого звена, а затем второго соединенного с ним.
В данном случае звено 1 совершает поступательное движение по прямой (подробнее такое движение рассмотрено ниже), а значит характеристики движения всех точек в данный момент одинаковы, т.е. 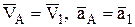 . При этом для точки А звена 1 это характеристики относительно неподвижной системы отсчета, т.е. абсолютные. Для этой же точки звена 2 (его можно принять материальной точкой) уже можно говорить о сложном движении, т.к. точка А скользит вдоль кулисы 3 (относительное движение) и поворачивается вместе с ней вокруг центра О (переносное). Таким образом, легко разложить найденные выше характеристики абсолютного движения на характеристики переносного и относительного движения точки А звена 2 (рис. 6).
. При этом для точки А звена 1 это характеристики относительно неподвижной системы отсчета, т.е. абсолютные. Для этой же точки звена 2 (его можно принять материальной точкой) уже можно говорить о сложном движении, т.к. точка А скользит вдоль кулисы 3 (относительное движение) и поворачивается вместе с ней вокруг центра О (переносное). Таким образом, легко разложить найденные выше характеристики абсолютного движения на характеристики переносного и относительного движения точки А звена 2 (рис. 6).

Учитывая, что 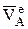 перпендикулярен
перпендикулярен  , последнее уравнение можно не проецировать на оси Х и Y, а сразу записать
, последнее уравнение можно не проецировать на оси Х и Y, а сразу записать
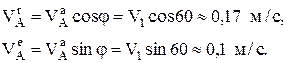
Если 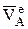 вращательная скорость точки А звена 2 и звена 3 с радиусом вращения ОА, то угловую скорость звена 3 можно найти так
вращательная скорость точки А звена 2 и звена 3 с радиусом вращения ОА, то угловую скорость звена 3 можно найти так
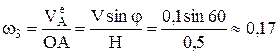 рад/с.
рад/с.
Аналогично рассуждая можно для ускорений получить с учетом (5) следующее
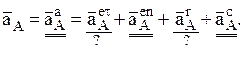
Здесь 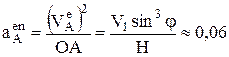 м/с2
м/с2
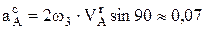 м/с2.
м/с2.
Спроецировав последнее векторное уравнение на оси Х и Y с учетом направлений векторов, показанных на рис. 6 получим
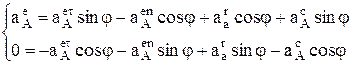 .
.
Можно обратить внимание, что взаимно перпендикулярные вектора 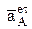 и
и 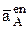 позволяют находить проекцию на одну ось через синус, а на другую ось через косинус одного угла j. То же справедливо и для одного какого-то вектора при его проецировании на ось Х, а затем ось Y .
позволяют находить проекцию на одну ось через синус, а на другую ось через косинус одного угла j. То же справедливо и для одного какого-то вектора при его проецировании на ось Х, а затем ось Y .
Решая последнюю систему относительно двух неизвестных 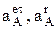 , т.е. модулей соответствующих векторов легко можно найти их значения. Если в результате расчетов значение окажется со знаком « - », то соответствующий вектор направлен противоположно направлению первоначально принятому на рис. 6 (вектора
, т.е. модулей соответствующих векторов легко можно найти их значения. Если в результате расчетов значение окажется со знаком « - », то соответствующий вектор направлен противоположно направлению первоначально принятому на рис. 6 (вектора 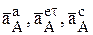 могут быть определены по направлению точно, по ранее рассмотренным правилам).
могут быть определены по направлению точно, по ранее рассмотренным правилам).
Угловое ускорение звена e3 совпадает с направлением вектора 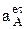 , а величина его находится с учетом радиуса вращения точки А звеньев 2 и 3, т.е.
, а величина его находится с учетом радиуса вращения точки А звеньев 2 и 3, т.е. 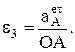
Дата добавления: 2018-05-10; просмотров: 1162;











