Динамика механической системы

Основные закономерности движения механической системы описываются общими теоремами динамики механической системы.

1. Механическая система. Силы внутренние и внешние.

Механической системой называется любая совокупность материальных точек, выделенная в данной задаче. Например, группа летящих самолётов вполне может рассматриваться как механическая система. Следует заметить, что и одна материальная точка, а также твёрдое тело могут считаться разновидностями механической системы.

Если между материальными точками существуют силы взаимодействия, то они называются внутренними и обозначаются .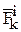

Следует отметить, что геометрическая сумма (главный вектор) внутренних сил равна нулю ввиду того, что они действуют в механической системе попарно: как действие и противодействие.

Таким образом:

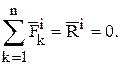
Главный момент системы внутренних сил также равен нулю в связи с тем, что внутренние силы действуют попарно по одной линии в разные стороны, следовательно, каждая пара имеет одно и то же плечо относительно любой точки. Моменты этих сил относительно любого центра будут равны по модулю, но будут иметь разные знаки.

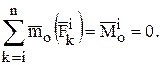
Внешними называются силы взаимодействия точек механической системы с телами или точками, не входящими в данную систему. Они обозначаются 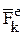. Геометрическая сумма этих сил называется главным вектором внешних сил.

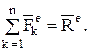
Механическая система, главный вектор внешних сил которой равен нулю, называется замкнутой.

Следует заметить, что понятие «главный вектор сил» является математической абстракцией, т.к. внешние и внутренние силы приложены к разным материальными точкам и реально сложены быть не могут.

2. Центр масс механической системы.

Центр масс механической системы это геометрическая точка, радиус–вектор которой определяется по формуле

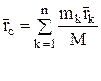. (7)

Представим эту формулу в более удобном виде:

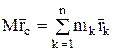(8)

или, проектируя на оси координат, запишем:

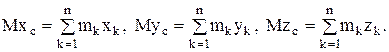(9)

Несомненным достоинством этого понятия является полная независимость от действия любых сил или систем сил. У твердого тела, находящегося в поле сил тяжести, центр масс совпадает с его центром тяжести.

3. Дифференциальные уравнения движения механической системы.

Основное уравнение движения отдельной материальной точки может быть записано в векторной форме:

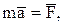(10)

а если она в составе механической системы, то, имея в виду деление сил на внешние и внутренние:

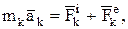(11)

где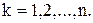

Число таких уравнений равно числу точек системы, а в проекциях на оси координат

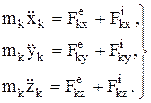(12)

Следует заметить, что внутренние силы входят в эти уравнения в весьма сложном виде. Они зависят друг от друга, от внешних сил, от координат и скоростей всех точек системы, поэтому аналитическое решение этих дифференциальных уравнений связано зачастую с непреодолимыми трудностями. Интегрирование этих уравнений численными методами с использованием ЭВМ хотя и расширяет круг решаемых задач, однако является более примитивным методом.

В то же самое время существует вполне определенный круг задач, где совершенно необязательно решать эти задачи в полном объёме относительно каждой точки. Кроме того, связи, наложенные на точки системы, позволяют сократить число неизвестных.

В механике разработаны методы, позволяющие обойти указанные трудности решения дифференциальных уравнений движения механической системы. Это дифференциальные уравнения движения механической системы в обобщенных параметрах, принципы механики и общие теоремы динамики системы: теорема о движении центра масс, теорема об изменении количества движения, теорема об изменении кинетического момента и теорема об изменении кинетической энергии.

3. Теорема о движении центра масс.

Сложим почленно правые и левые части уравнения (11):

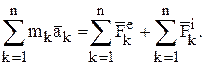
Запишем левую часть в несколько иной форме:

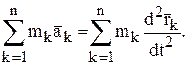
Так как масса каждой точки во время движения остаётся неизменной, внесём её под знак производной:

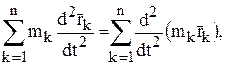
а так как сумма производных равна производной суммы, поменяем местами знаки суммирования и дифференцирования:

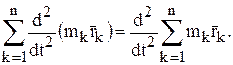
Замечая, что сумма в этом выражении на основании формулы (8) равна 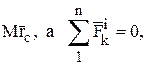запишем окончательно:

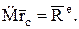(13)

Это уравнение выражает теорему о движении центра масс механической системы, а сравнение выражений (10) и (13) позволяет сформулировать теорему: центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса механической системы и к которой приложены все внешние силы, действующие на систему.

Это утверждение позволяет сделать мотивированное разграничение понятий: материальная точка и материальное тело, а именно: если нас интересуют угловые перемещения объекта, то его следует отнести к понятию «материальное тело», а если нет, и мы интересуемся только положением его центра масс, то объект можно считать материальной точкой.

Следствия из теоремы.

1. Внутренние силы непосредственно не влияют на движение центра масс механической системы. Это заключение, вытекающее из формулы (13), позволяет отвергать как совершенно бесперспективные различные проекты устройств, которые перемещались бы исключительно внутренними силами.

2. Центр масс замкнутой механической системы движется равномерно и прямолинейно, т.к. при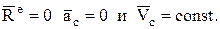

3. Если проекция главного вектора внешних сил на какую-нибудь ось (например, ось х) равна нулю, то 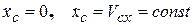, а если, кроме того, при t=0 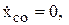то 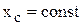, то есть центр масс при этом вдоль оси х перемещаться не будет.

Итак, теорема о движении центра масс исключает из рассмотрения все внутренние силы, но при этом позволяет решить задачу только лишь в отношении некоторой геометрической точки, а решение задачи о движении материальных точек связывается при этом с определенными условиями их перемещений.

Пример 2

На одном конце лодки, находящейся в покое, в точке А стоит человек, он переходит затем на другой её конец в точку В. Определить, пренебрегая сопротивлением воды, на какое расстояние передвинется при этом лодка, если вес лодки равен Р, вес человека равен Q.

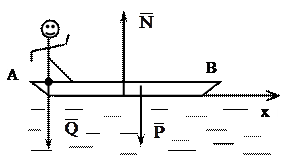Решение: На основании следствия из теоремы о движении центра масс, замечая что проекции всех сил на ось х равны нулю, имеем V_cx=C₁, а поскольку С₁=0, то х_с=С₂, т. е. центр масс системы останется на месте. Запишем равенство, определяющее положение центра масс в начале движения

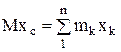
и в конце движения

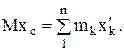
Вычтем из первого равенства второе

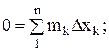
умножая на g, получим

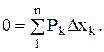
Подставим данные

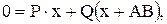
получим

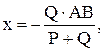
знак «-» указывает на то, что лодка передвинется влево.

Контрольные вопросы

1. Что называется механической системой?

2. Что такое центр масс механической системы?

3. Как формулируется теорема о движении центра масс?

4. Как движется центр масс замкнутой механической системы?

4. Количество движения механической системы.

Количество движения отдельной материальной точки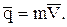

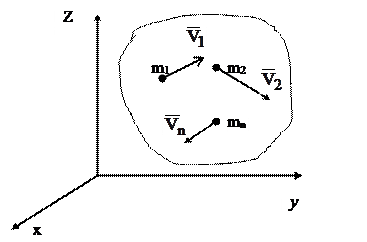
Количество движения механической системы определяется как геометрическая сумма количеств движения материальных точек, составляющих систему:

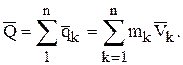(14)

Это выражение можно несколько усовершенствовать, пользуясь теми же приёмами, что использовались в доказательстве предыдущей теоремы:

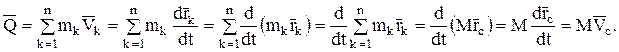(15)

4. Импульс силы.

В связи с тем, что эффект действия силы связан не только с её величиной и направлением, но и с продолжительностью действия, введем в рассмотрение меру действия силы – импульс силы:

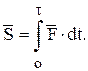
Если сил несколько, то аналогично понятию «главный вектор» вводится понятие «главный импульс» внешних сил.

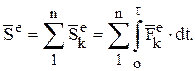(16)

5. Теорема об изменении количества движения

Используя формулу (13), запишем:

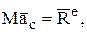
но 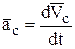, тогда

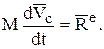
Так как масса системы неизменна во всё время движения, её можно внести под знак производной:

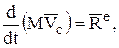
и окончательно:

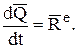(17)

Это и есть математическая запись теоремы об изменении количества движения в дифференциальной форме.

Производная по времени от количества движения механической системы равна главному вектору внешних сил.

Разделив неизвестные и проинтегрировав, получим выражение

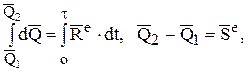(18)

где Q₂ – количество движения механической системы при ;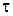

Q₁ – количество движения механической системы в начале отсчета;

S^e – главный импульс внешних сил за время .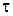

Приращение количества движения механической системы за время 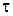равно главному импульсу внешних сил на то же время.

Следствия из теоремы

1. Внутренние силы непосредственно не изменяют количества движения механической системы.

2. Количество движения замкнутой механической системы есть величина постоянная. Действительно: при 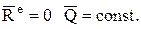Это следствие иногда называют законом сохранения количества движения.

3. При равенстве нулю проекции главного вектора внешних сил на какую-нибудь ось (например, х) проекция количества движения на эту ось есть величина постоянная.

Необходимо отметить также, что количество движения не является универсальной мерой движения. Например, при движении механической системы вокруг неподвижного центра масс количество движения остаётся равным нулю, а все материальные точки в это время могут двигаться.

Пример 3

Определить горизонтальную составляющую N возникающего при движении воды давления на опору колена трубы диаметром d, по которой течет вода со скоростью V. Плотность воды – r.

Решение. Применим для решения этой задачи теорему об изменении количества движения в интегральной форме

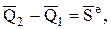
а в проекции на ось Х

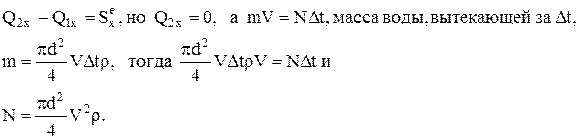
Контрольные вопросы

1. Как определяется количество движения механической системы?

2. Что такое импульс силы?

3. Как формулируется теорема об изменении количества движения?

4. Как формулируется закон сохранения количества движения?

5. Чему равно количество движения тела, вращающегося вокруг неподвижного центра масс?

6. Момент количества движения материальной точки.

Эта мера движения вводится по аналогии с моментом силы относительно центра и оси. Моментом силы относительно центра О является векторное произведение:

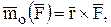
а моментом силы относительно оси Z является проекция вектора – момента ­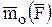 на ось Z:

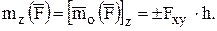
Момент количества движения точки относительно центра О соответственно:

,

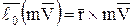а момент количества движения относительно оси Z

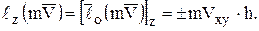
При этом знак “+” будет в том случае, когда со стороны оси виден поворот векторов 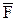и 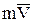против часовой стрелки.

7. Кинетический момент системы

Главный момент количества движения механической системы, который обычно называют кинетическим моментом относительно центра, определится как геометрическая сумма моментов количеств движения материальных точек относительно центра:

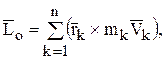
а алгебраическую сумму моментов количеств движения относительно оси называют кинетическим моментом относительно оси:

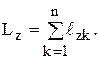
8. Обобщенная теорема моментов

Если точка о (центр моментов) движется произвольно, то кинетический момент относительно центра О равен:

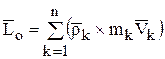. (19)

Возьмём производную по времени от этого выражения:

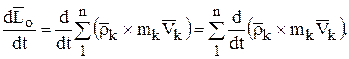
Имея в виду, что 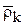и 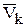величины переменные, имеем:

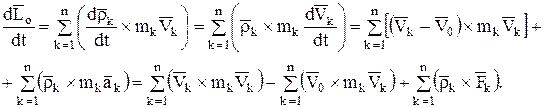
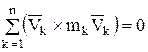как векторное произведение коллинеарных векторов.

Преобразуем суммы:

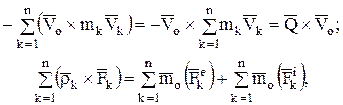
но ,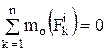

тогда: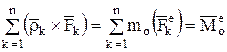

и окончательно получим:

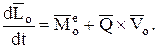(20)

Это и есть математическая запись обобщенной теоремы моментов.

Производная по времени от кинетического момента относительно центра О равна сумме главного момента внешних сил относительно того же центра и векторного произведения количества движения механической системы на скорость центра моментов.

9. Частные случаи теоремы моментов

1. Если центр моментов неподвижен, то 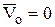и ,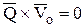

тогда

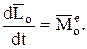(21)

Это выражение следует назвать теоремой моментов относительно неподвижного центра.

2. Если центр моментов совпадает с центром масс механической системы, то

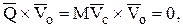
при этом

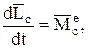(22)

а это выражение есть теорема моментов относительно центра масс.

3. Если центр моментов имеет скорость, коллинеарную скорости центра масс:

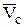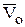║ , то

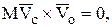
тогда

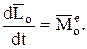(23)

Этот частный случай весьма продуктивен при решении задач, где в качестве центра моментов целесообразно использовать точку, движущуюся параллельно центру масс, например, точку касания катящегося колеса.

В этом случае удаётся исключить неизвестные реакции, возникающие в этой точке.

Пример 4

Горизонтальной платформе радиуса r весом Р, имеющей вертикальную ось, проходящую через центр платформы О, сообщается начальная угловая скорость w₀. Человек А весом Q, находившийся в начальный момент в центре платформы, идет вдоль радиуса ОВ. Найти угловую скорость вращения платформы w при ОА=r, принимая платформу за однородный диск.

Решение. Используем для решения теорему об изменении кинетического момента относительно неподвижного центра

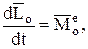
спроектируем это равенство на ось вращения Z

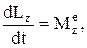
но 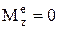, тогда L_z=const.

В начальный момент

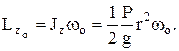
В конце движения

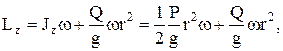
приравнивая правые части

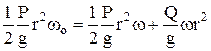
и сократив на 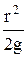, получим

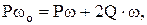
откуда

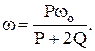
Итак, доказаны три теоремы динамики системы, которые ставят в соответствие векторные меры движения 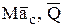и 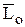векторным же мерам действия сил 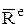и 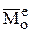. Во всех трёх теоремах исключены внутренние силы.

Контрольные вопросы

1. Как определяется момент силы относительно центра и оси?

2. Как определяется момент количества движения материальной точки относительно центра и оси?

3. Что такое кинетический момент механической системы?

4. Как формулируются частные случаи теоремы моментов?

Переходим к рассмотрению четвертой теоремы. Эта теорема по сравнению с тремя предыдущими имеет ряд особенностей: во-первых, она связывает между собой скалярные меры движения со скалярными мерами действия сил, во-вторых, в ней не исключены внутренние силы, и в-третьих, доказанная для одной точки, она распространяется на всю механическую систему.

10. Кинетическая энергия

Кинетической энергией материальной точки будем называть половину произведения массы точки на квадрат её скорости:

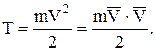
Эта величина всегда положительна, и поэтому кинетическую энергию механической системы будем определять как арифметическую сумму кинетических энергий отдельных точек:

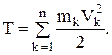
Скалярной мере движения необходимо поставить в соответствие скалярную меру действия сил.

15. Работа и мощность силы

Работу постоянной силы на конечном прямолинейном перемещении из точки М₁ в точку М₂ можно представить следующим образом:

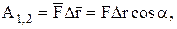
или

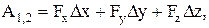
где F_x, F_y, F_z – проекции вектора 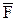на оси x, y, z;

∆x, ∆y, ∆z – проекции вектора 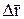на те же оси.

Если же требуется определить работу на криволинейном перемещении точки приложения переменной силы, то следует всё это конечное перемещение разбить на бесконечно большое количество бесконечно малых участков, определить работу на каждом участке, а затем эти работы просуммировать.

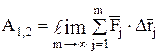(24)

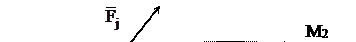
Произведение под знаком суммы при бесконечном уменьшении 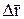называется элементарной работой:

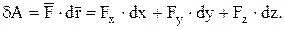
В общем случае выражение в правой части равенства не является полным дифференциалом некоторой функции координат, т. к. сила может быть функцией скорости или времени.

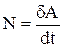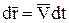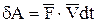Ещё одной скалярной мерой действия сил является мощность – это отношение элементарной работы к дифференциалу времени: , имея в виду, что , а , запишем:

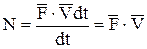, (25)

или

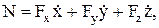
где 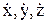– проекции скорости на оси координат x, y, z.

11. Теорема об изменении кинетической энергии

Запишем основное уравнение динамики точки:

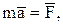
или

.

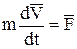Умножим скалярно правую и левую части равенства на :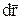

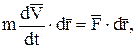
замечая, что 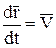, запишем:

.

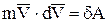Имея в виду, что

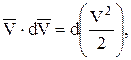
получим:

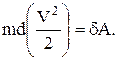
Так как масса точки во время движения не меняется, то

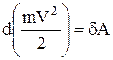
и окончательно получим:

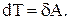(26)

Дифференциал кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.

Разделив правую и левую части на dt, получим:

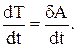
В правой части записано выражение, определяющее мощность всех сил, приложенных к материальной точке:

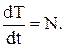(27)

Таким образом, формулировка второй дифференциальной формы теоремы энергии может быть записана следующим образом: «Производная по времени от кинетической энергии материальной точки равна мощности сил, приложенных к точке».

Третья, интегральная, форма теоремы может быть получена интегрированием правой и левой части равенства (18) в пределах от М₁ до М₂ по траектории перемещения материальной точки:

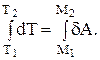(28)

Правая часть равенства представляет собой работу сил, приложенных к точке, тогда

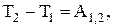(29)

т. е. изменение кинетической энергии материальной точки на некотором перемещении равно работе сил, приложенных к этой точке на том же перемещении.

Следует заметить также, что интеграл в правой части равенства (28) в общем случае имеет вид

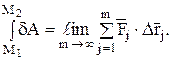
Полученную теорему, не изменяя обозначений, можно распространить и на механическую систему, имея в виду, что кинетическая энергия определяется для всей системы, а работа подсчитывается для внешних и внутренних сил.

Пример 5

На шкив радиуса r весом Q, вращающийся вокруг горизонтальной оси О, навернута веревка, к концу которой привязана гиря весом Р; в начале система находится в покое. Найти угловую скорость шкива в тот момент, когда груз опустится на расстояние h.

Решение: Применим теорему об изменении кинетической энергии Т₂-Т₁=А_1,2. Но Т₁=0, тогда Т₂=А_1,2

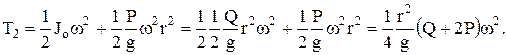
Работу совершает только сила тяжести груза

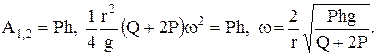
Библиографический список

1. Айзерман М.А. Классическая механика. М.: Наука, 1974. 368 с.

2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. М.: Наука, 1970. Т.2. 460 с.

3. Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 1995. 415 с.

4. Яблонский А.А. Курс теоретической механики. М.: Высшая школа, 1971. Ч. 1. 275 с.

5. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. М.: Высшая школа, 1983. 532 с.

6. Сборник заданий для курсовых работ по теоретической механике. Учеб. пособие для вузов./ Под ред. А.А Яблонского. и др. М.: Высшая школа, 1985. 367 с.

7. Бать М.И. и др. Теоретическая механика в примерах и задачах /М.И.Бать, Г.Ю.Джанелидзе, А.С.Кельзон. М.: Физматгиз, 1961. Ч.1. 457 с.

8. Мещерский Н.В. Сборник задач по теоретической механике. М.: Наука, 1971. 450 с.