Система связанных тел
Во многих инженерных задачах приходится рассматривать равновесие не только одного тела, но и равновесие некоторой конструкции состоящей из нескольких тел. В этом случае приходится рассматривать равновесие каждого тела в отдельности, учитывая при этом силы, которыми действуют друг на друга тела, входящие в рассматриваемую систему. Тела могут быть соединены между собой с помощью шарнира, соприкасаться друг с другом и взаимодействовать одно с другим, вызывая определение силы взаимодействия. Эти силы, согласно аксиоме равенства действия и противодействия, всегда равны по модулю и противоположны по направлению.
Силы, с которыми тела, входящие в данную систему, действуют друг на друга, называются внутренними силами этой системы. Все остальные силы, включая сюда и реакции опор, называются внешними силами системы.
Если система находится в покое, то силы, приложенные к каждому из твердых тел, входящих в данную систему, уравновешиваются и, следовательно, для каждого из этих тел можно составить уравнения равновесия. В эти условия равновесия, для каждого тела в отдельности, войдут не только внешние силы, но и внутренние. Если же мы составляем уравнения равновесия для системы в целом, то внутренние силы, представляющие уравновешенную систему сил, в данные уравнения не войдут. Так для схемы, приведенной на рис. 12, 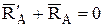 .
.
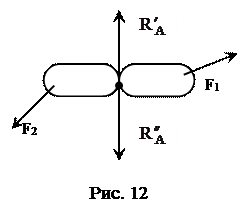 При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему на отдельные твердые тела, добавляя при этом к внешним силам, силы взаимодействия между телами (внутренние силы) и составлять соответственно уравнения равновесия для каждого тела. Учитывая при этом, что для равнодействующей внутренних сил неизвестен не только модуль, но и направление, их обычно представляют в виде двух составляющих, направленных по двум осям координат. Таким образом, для системы, состоящей из N тел, когда на каждое тело действует плоская система сил, можно составлять 3N уравнений равновесия и, следовательно, определять 3N неизвестных.
Задача 4
Составная балка состоит из двух участков АС и СД, соединенных в точке с шарниром (рис. 13). В точке А – неподвижная опора, в точке В – подвижная опора, конец Д балки поддерживается с помощью вертикальной тяги ДЕ. К балке СД приложена вертикальная сила F. Найти реакцию в шарнире ДЕ. Известно 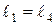 и
и 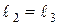 .
.
Решение: Используя принцип освобождаемости от связей, заменим действие связей соответствующими реакциями. Реакцию в шарнире А представим в виде двух составляющих XA и YA . Реакцию подвижной опоры обозначим RB , а реакцию нити – Т. В шарнире С разделим балку на два тела: стержень АС и стержень СД и для каждого участка в точке С обозначим равнодействующую внутренних сил в виде XC , YC и 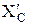 ,
, 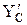 .
.
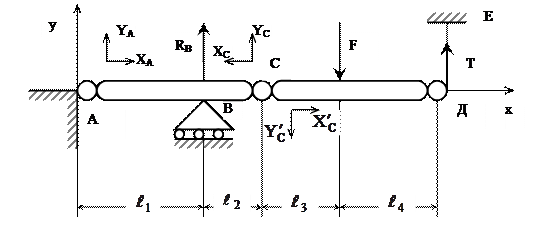

Рис. 13
Составим уравнения равновесия для участка АС
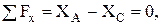 (1)
(1)
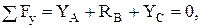 (2)
(2)
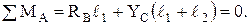 (3)
(3)
Уравнения равновесия для участка СД
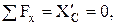 (4)
(4)
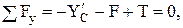 (5)
(5)
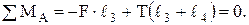 (6)
(6)
Учитывая равенства 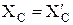 и
и 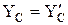 получим:
получим:
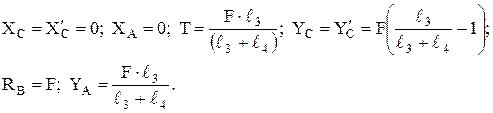
Задача 5
Для данной стержневой конструкции, представленной на рис. 14, определить величины опорных реакций.
Решение: Стержневая конструкция состоит из двух частей АС и ВС. Используя принцип освобождаемости от связей, заменим опоры их реакциями. Для жестко защемленной опоры А имеем три составляющих опорной реакции, для шарнирно подвижной опоры В – одну опорную реакцию. В точке разделения конструкции С имеем по две составляющих (для каждого участка) реакций внутренних связей, который будут попарно равны по модулю и противоположны по направлению.
Составим уравнения равновесия для участка АС.
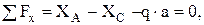 (1)
(1)
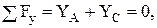 (2)
(2)
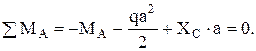 (3)
(3)
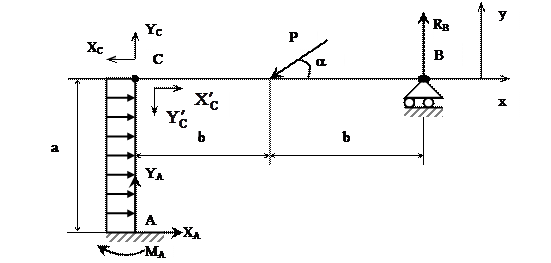

Рис. 14
Составим уравнения равновесия для участка ВС.
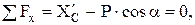 (4)
(4)
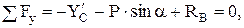 (5)
(5)
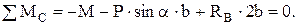 (6)
(6)
Из полученных шести уравнений, учитывая при этом равенства 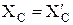 ,
, 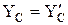 можно найти величины опорных реакций.
можно найти величины опорных реакций.
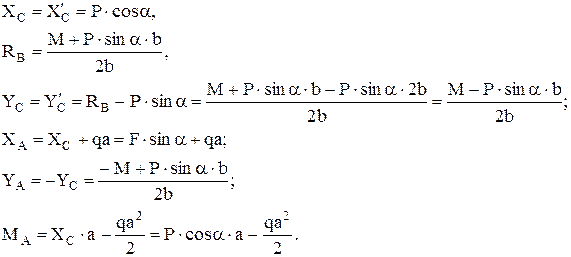
Дата добавления: 2018-05-10; просмотров: 1025;











