Произвольная система сил
Произвольной будем называть систему сил линии действия, которых расположены как угодно в пространстве. При изучении произвольной системы сил необходимо ознакомиться с понятием момента силы относительно оси.
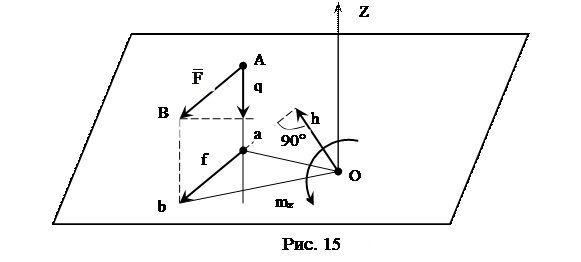
Пусть известна сила F, произвольно расположенная в пространстве. Разложим эту силу на две составляющие: одну параллельную оси Z, и другую f, лежащую на плоскости перпендикулярной оси Z. Опустим перпендикуляр на линию действия силы f и обозначим его h (рис. 15). Мерой вращательного эффекта, создаваемого силой f, будет служить момент силы относительно точки пересечения оси Z с плоскостью. Следовательно, величиной момента силы будет являться взятое с соответствующим знаком произведение mz = ±f∙h.
Из определения момента и из рис. 15 можно сделать следующие выводы:
1. Момент силы относительно оси равен нулю в том случае, когда линия действия силы пересекает ось или когда сила параллельна этой оси.
2. Момент силы относительно данной оси не изменяется при переносе точки приложения силы в любую другую точку на линии её действия.
 |
Уравнения равновесия, для произвольно расположенной в пространстве системы сил, получаются из условий, что главный вектор и главный момент равны нулю, т.е. 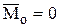 и
и 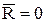 . Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.
. Эти уравнения равновесия формулируются следующим образом: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из трех координатных осей и суммы моментов относительно этих осей были равны нулю.
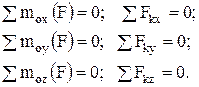
Контрольные вопросы:
1. Как Вы сформулируете понятие силы?
2. Что такое реакция связи?
3. Что такое проекция силы на ось?
4. Определить равнодействующую систему сходящихся сил?
5. Условия равновесия системы сходящихся сил.
6. Определить момент силы относительно точки?
7. Что такое пара сил и какими свойствами она обладает?
8. Указать формы условий равновесия плоской системы сил.
9. Каким образом решается задача на систему связанных тел?
10. Как определяется момент силы относительно оси?
11. Условия равновесия произвольной системы сил.
КИНЕМАТИКА
Кинематика является разделом теоретической механики, в котором рассматривается движение тела без учета действующих на него сил. В кинематике решаются следующие задачи: 1) задание движения и изучение кинематических характеристик всего тела; 2) изучение движения каждой из точек в отдельности.
Кинематика точки
Наиболее распространены два способа задания движения точки, причем под точкой часто понимают так называемую материальную точку, т.е. тело, размерами которого в данной задаче можно пренебречь. Последнее справедливо при поступательном (параллельно самому себе) движении тела по прямой и при движении по кривой, когда радиус кривизны траектории много больше размеров тела.
Итак координатный способ предполагает задание координат точки, например точки А, как функций времени.
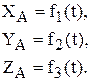 (1)
(1)
Уравнения движения (1) позволяют построить траекторию, например, по точкам изменяя время с заданным шагом. Они также дают возможность определить скорость 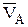 и ускорение
и ускорение 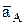 точки в любой момент времени, как по величине, так и по направлению.
точки в любой момент времени, как по величине, так и по направлению.
Проекции данных векторов на оси определяются дифференцированием (1) и последующей подстановкой времени, а модули их как корень квадратный из суммы квадратов проекций. При этом, если проекция получается отрицательной, это означает, что соответствующая составляющая вектора направлена против оси (направление осей должно быть задано предварительно, вместе с уравнениями (1)). Рассмотрим пример определения 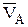 ,
, 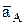 при t=1 c, когда (1) имеет вид
при t=1 c, когда (1) имеет вид
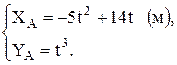 ,
,
где при t=1 c, XA=9 м, YA=1 м.
Тогда из уравнений движения следует (рис. 1)
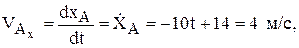
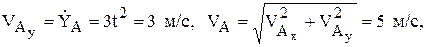 (2)
(2)

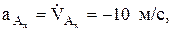
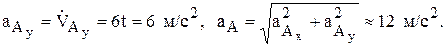 (3)
(3)
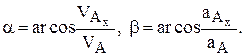
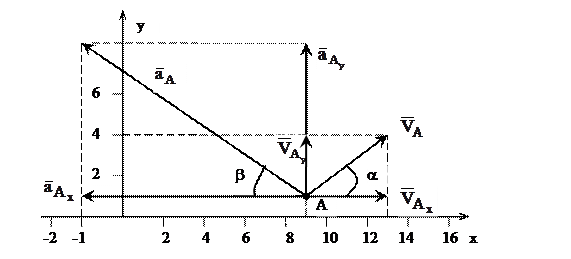

Рис. 1
При втором способе задания движения точки, называемом естественным, задают траекторию и начало отсчета пути точки по ней, а так же путь S по траектории в виде функции времени. В этом случае скорость 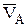 и касательное ускорение
и касательное ускорение 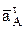 всегда касательные к траектории в рассматриваемой точке, а по величине определяются дифференцированием S=f(t), т.е.
всегда касательные к траектории в рассматриваемой точке, а по величине определяются дифференцированием S=f(t), т.е. 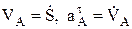 . Знак «-», полученный после дифференцирования подставки заданного значения времени t, показывает, что данный вектор
. Знак «-», полученный после дифференцирования подставки заданного значения времени t, показывает, что данный вектор 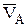 или
или 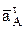 направлены в сторону убывания пути или криволинейной координаты S. Полное ускорение точки складывается из касательного и нормального ускорения
направлены в сторону убывания пути или криволинейной координаты S. Полное ускорение точки складывается из касательного и нормального ускорения 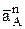 , которое направлено по нормали (перпендикулярно касательной) в сторону центра кривизны траектории. По величине последнее ускорение зависит от радиуса кривизны траектории в данной точке r, т.е.
, которое направлено по нормали (перпендикулярно касательной) в сторону центра кривизны траектории. По величине последнее ускорение зависит от радиуса кривизны траектории в данной точке r, т.е. 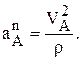
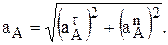 (4)
(4)
Физический смысл этих двух составляющих полного ускорения в том, что 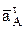 – характеризует интенсивность изменения вектора
– характеризует интенсивность изменения вектора 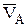 по величине, а ускорение
по величине, а ускорение 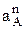 – по направлению. Рассмотрим пример, когда S=-5t2+14t (м) и необходимо определить
– по направлению. Рассмотрим пример, когда S=-5t2+14t (м) и необходимо определить 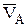 и
и 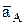 при t=1 c, когда траектория точки представляет собой дугу радиусом R=18 м (рис. 2).
при t=1 c, когда траектория точки представляет собой дугу радиусом R=18 м (рис. 2).
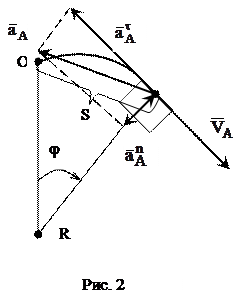 S=-5∙12+14∙1 = 9 м,
S=-5∙12+14∙1 = 9 м, 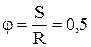 рад » 30°
рад » 30°
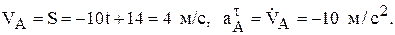
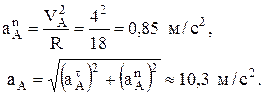
Если при координатном способе задания движения точки необходимо найти 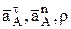 , то используется следующие формулы:
, то используется следующие формулы:
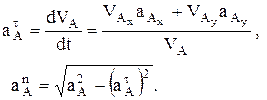
Дата добавления: 2018-05-10; просмотров: 797;











