Идеально сбалансированные бинарные деревья

Использование деревьев для организации данных, с которыми требуется выполнять операции поиска, вставки и удаления, оказывается более предпочтительным чем использование списков.

Пусть каждый элемент данных d содержит поле ключа d.key (или в других обозначениях key(d) или k(d)), который используется для сравнений в ходе операций поиска.

Рассмотрим так называемые идеально сбалансированные деревья. Идеально сбалансированным назовем такое бинарное дерево T , что для каждого его узла x справедливо соотношение |n_L(x) - n_R(x)| £ 1, где n_L(x) - количество узлов в левом поддереве узла x, а n_R(x) - количество узлов в правом поддеревеузла x. Примеры некоторых идеально сбалансированных деревьев даны на рисунке.

В идеально сбалансированном дереве число узлов n и высота дерева h связаны соотношением 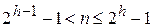, или в другой форме 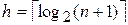. (Здесь и далее высота дерева определена так, что при n = 0 имеем h = 0, а при n = 1 имеем h = 1.)

Рассмотрим алгоритм построения идеально сбалансированного дерева по последовательности данных a₁, a₂, …, a_n (например, находящейся в файле f_input). Идея этого рекурсивного алгоритма ясна из следующего рисунка (здесь n_L = n div 2 и n_R = n – n_L – 1, т. е. n = n_L + n_R +1)

type BTree = ­Node;

Node = record

Info: Elem;

L, Rb: BTree

end {Node}

Тогда алгоритм, реализованный в виде рекурсивной функции, есть

function Tree (n: Nat0): BTree;

var nL, nR: Nat0; b1, b2: BTree; x: Elem;

begin if n = 0 then Tree := nil else

begin nL := n div2; nR := n – nL – 1;

b1 := Tree (nL);

Read (f_input, x);

b2 := Tree (nR);

Tree := ConsBT (x, b1, b2)

End

end{Tree}

Здесь ConsBT (x, b1, b2) - функция-конструктор, строящая новое дерево из корня x и левого b1 и правого b2 поддеревьев.

Рассмотрим примеры работы этого алгоритма. Пусть во входном файле находится последовательность a, b, c, d, e, f, g, h, i, а стартовый вызов функции Tree (n) производится так: Reset(f_input); b := Tree (n). На рисунке представлены деревья, построенные с помощью функции Tree (n) при значениях n = 1, 2, 3, 4, 5, 6, 7, 8, 9.

Отметим, что данный алгоритм строит такие идеально сбалансированные деревья, что n_L(x) - n_R(x) = 0 или 1, т. е. при n_L(x) ≠ n_R(x) именно левое поддерево содержит на один узел больше. При этом структура дерева определяется только значением параметра n, а содержимое узлов зависит от расположения элементов во входной последовательности. В предыдущем примере из-за того, что входная последовательность упорядочена, все построенные деревья обладают интересным свойством: исходная упорядоченная последовательность порождается при обходе этих деревьев «слева направо», т. е. при симметричном или ЛКП-обходе.

Если бы входная последовательность не была упорядочена, то построенное функцией Tree дерево не обладало бы отмеченным свойством упорядоченности.

Деревья, в результате ЛКП-обхода которых получается упорядоченная последовательность узлов, называются деревьями поиска и будут подробно рассмотрены далее.