ЛЕКЦИЯ 18. АВЛ-ДЕРЕВЬЯ
Цели и задачи лекции..ознакомиться с АВЛ-деревьями
Основные рассматриваемые вопросы:балансировка АВЛ-дерева.
Критерий идеальной сбалансированности дерева. Дерево называется идеально сбалансированным, если все его уровни, за исключением, может быть, последнего, полностью заполнены. (В бинарном дереве полностью заполненный уровень n содержит 2n узлов).
Если дерево поиска близко к сбалансированному, то даже в худшем случае за время порядка O(logn) в нем можно:
1.Найти вершину с заданным значением или выяснить, что такой вершины нет.
2.Включить новую вершину.
3.Исключить вершину.
Среднее время выполнения этих операций будет также близким к O(log2n), так как в идеально сбалансированном дереве при полностью заполненных уровнях на последнем уровне находится больше половины узлов дерева. Например, последовательность значений 4, 6, 2, 1, 5, 3, 7 дает следующее идеально сбалансированное дерево:
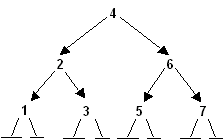
В этом дереве 7 узлов, на последнем уровне находится 4 узла. Если доступ к одному узлу требует 1 единицу времени, то до узла <4> можно добраться за 1 единицу времени, до <2> и <6> - за 2, до <1>, <3>, <5>, <7> - за 3. То есть в худшем случае требуется 3 единицы времени, в среднем: (1+2*2+3*4)/7 = 2.4 единицы времени.
Однако значения в последовательности могут идти и в другом порядке, что может привести к построению несбалансированного дерева. В худшем случае можно получить вырожденное дерево, подобное линейному списку. Например, последовательность значений 1, 7, 2, 6, 3, 5, 4 дает следующее вырожденное дерево:
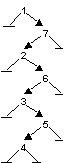
Работа с таким вырожденным деревом потребует в худшем случае 7 единиц времени (доступ к <4>), а в среднем: (1+2+3+4+5+6+7)/7 = 4 единицы времени. То есть для вырожденного дерева затраты на доступ к узлам в худшем случае имеют порядок O(n), в среднем - O(n/2).
Разница во времени доступа будет гораздо заметнее при большем числе узлов. Например, в идеально сбалансированном дереве из 1023 узлов время доступа в худшем случае будет равно 10 единицам времени, в среднем:
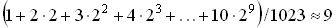 единицам времени.
единицам времени.
А в вырожденном дереве из 1023 узлов потребуется в худшем случае 1023 единицы времени, в среднем - 512 единиц времени.
Поэтому при работе с деревьями поиска больших размеров крайне желательно, чтобы они были близки к сбалансированным.
Приведение уже существующего дерева к идеально сбалансированному - процесс сложный. Проще балансировать дерево в процессе его роста (после включения каждого узла). Однако требование идеальной сбалансированности делает и этот процесс достаточно сложным, способным затрагивать все узлы дерева.
АВЛ-деревья
В 1962 году советские математики Адельсон-Вельский Г.М. и Ландис Е.А. предложили метод балансировки, требующий после включения или исключения узла лишь локальные изменения вдоль пути от корня к данному узлу, то есть времени не более O(log2n). При этом деревьям разрешается отклоняться от идеальной сбалансированности, но в небольшой степени, чтобы среднее время доступа к узлам было лишь немногим больше, чем в идеально сбалансированном дереве. Такие деревья называются АВЛ-деревьями.
Критерий сбалансированности АВЛ-дерева. Дерево называется сбалансированным тогда и только тогда, когда для каждого его узла высоты его левого и правого поддеревьев отличаются не более чем на единицу.
Примеры АВЛ-сбалансированных деревьев:
| Уровень 0 Уровень 1 Уровень 2 Уровень 3 | 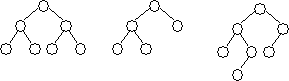
|
Примеры деревьев, не являющихся АВЛ-сбалансированными:
| Уровень 0 Уровень 1 Уровень 2 Уровень 3 | 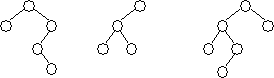
|
Для каждого узла дерева можно определить показатель сбалансированности как разность между высотой правого и левого поддерева данного узла. Пусть hR - высота правого поддерева, - высота левого. Тогда показатель сбалансированности есть hR - hL.
Если дерево АВЛ-сбалансировано, то для каждого узла выполняется: |hR - hL| <= 1. Если хотя бы для одного узла дерева это не так, то дерево не является АВЛ-сбалансированным. Приведем примеры АВЛ-сбалансированного и АВЛ-несбалансированного дерева (у каждого узла указан показатель сбалансированности):
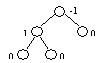 АВЛ-сбалансированное дерево
АВЛ-сбалансированное дерево
| 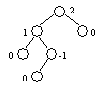 АВЛ-несбалансированное дерево
АВЛ-несбалансированное дерево
|
Дата добавления: 2018-05-10; просмотров: 1585;











