Эффекты, возникающие при движении заряженных частиц в магнитном поле

1.Магнитная гидродинамика (МГД) – это раздел физики, изучающий движение электропроводящих газов и жидкостей во взаимодействии с магнитным полем.

Обычно электропроводящая подвижная среда называется плазмой. Однако такой средой может быть не только ионизированный в той или иной степени квазинейтральный газ, но и жидкие металлы, расплавы солей и другие жидкие электролиты.

В общих задачах магнитной гидродинамики плазма рассматривается как связанный коллектив заряженных частиц. Но для качественного уяснения большинства эффектов достаточно рассмотреть движение в магнитном поле отдельных как бы изолированных частиц плазмы.

2.МГД – насос. В начале 19 века Гемфри Дэви поставил опыт, в котором впервые была реализована идей МГД – насоса.

Круглый металлический стакан с жидкой ртутью помещался между полюсами магнита (рис.101). Когда от осевого электрода к стенкам сосуда идёт электрический ток, ртуть вращается.

В жидких металлах носителями электрических зарядов являются не только электроны проводимости, но и вся масса положительно заряженных ионов металла. Под действием электрического поля источника тока возникает дрейф как электронов проводимости в одну сторону, так и ионов металла в другую. Действующая на заряженные частицы магнитная сила Лоренца направлена в одну сторону. Она и создаёт круговое течение ртути.

Принцип МГД – насоса используется в настоящее время для перекачки теплоносителя в первичных теплоотводящих контурах. Из-за высокой плотности тепловыделения в таких реакторах в качестве теплоносителя часто используются жидкие металлы – натрий или смесь натрия с калием.

В трубопровод теплоотводящего контура встраивается участок, состоящий из двух противоположно расположенных электропроводящих пластин 1 и 2 (рис.102) и двух электроизолирующих пластин 3 и 4. Участок помещается в постоянное магнитное поле B, а через жидкий металл пропускается постоянный электрический ток I.

Действующая на ионы и электроны сила Лоренца направлена в одну сторону (вправо на рис.102) и складывается в общую силу Ампера 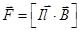. Обусловленное этой силой давление p = FçS, где S - сечение трубы, создаёт постоянное течение теплоносителей в контуре.

3.МГД – генераторы. Их действие противоположно действию МГД – насосов. Плазма с температурой несколько тысяч градусов, генерируемая химическим источником, например, ракетным двигателем, продувается в трубе в магнитном поле (рис.103).

Под действием силы Лоренца положительно заряженные частицы плазмы смещаются в одну сторону (вверх на рис.103), а отрицательные частицы – в другую. Между проводящими пластинами 1 и 2 возникает разность потенциалов. Если к пластинам подключить нагрузку R, в цепи потечёт ток I.

В результате установка может работать как источник постоянного тока. Их КПД достигает 40-50%. Такие МГД – генераторы удобны тем, что в качестве источника плазмы в них могут использоваться как химические, так и ядерные источники энергии.

Мощность опытных МГД генераторов, созданных в США в 60-е годы XX в. на базе ракеты “Атлас”, около 10 МВт. Установка У-25, разработанная в СССР в то же время, имела мощность до 25 МВт. Температура плазмы в этих установках составляла 1200-1250°С.

Широкому промышленному внедрению МГД – генераторов препятствует короткий срок службы источников плазмы, что приводит к росту себестоимости получаемой энергии, и высокое акустическое давление, возникающее в зоне работы этих источников.

4.Эффект Холла открыл в 1879 г. американец Эдвин Холл, работая с тонкими плёнками золота.

Рассмотрим проводник с током в магнитном поле. Придадим проводнику форму прямоугольного параллелепипеда, две грани которого параллельны вектору напряжённости электрического поля E, создаваемого источником тока, а две других грани – параллельны вектору магнитной индукции поля B (рис.104).

На каждый заряд проводимости действует сила Лоренца 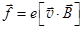. Если носители тока – положительные заряды, то верхняя грань проводника на рис.104 заряжается положительно, а нижняя – отрицательно. Между поверхностями проводника возникает разность потенциалов U_x = E_x×l, где l - расстояние между гранями проводника (толщина проводника).

Холловская напряжённость электрического поля E_x найдётся из условия стабилизации перераспределения зарядов, когда магнитная сила Лоренца уравновешивается силой возникающего электрического поля.

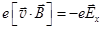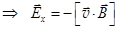, . (15.1)

Эффект Холла позволяет получить информацию о знаке и концентрации носителей электрического тока в проводниках. Если выразить скорость дрейфа v носителей электрического тока из формулы плотности j = env и подставить в (15.1), то 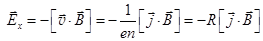. (15.2)

Величину R = 1çen называют коэффициентом Холла. Измерив R, можно найти концентрацию n носителей тока в проводнике.

Знак холловской разности потенциалов позволяет судить о знаке носителей тока. Если носители тока – отрицательные заряды, то верхняя грань проводника на рис.104 будет приобретать не положительный, а отрицательный потенциал (рис.105).

Опыты показали, что все щелочные металлы, а также Cu, Ag, Au, Mg, Ca, Hg, Al, Ga, In, Ti, Mn, Ni, Sn, Pd, Bi, Pt имеют отрицательный холловский потенциал. Носителями тока в этих металлах являются электроны проводимости.

Но оказалось так же, что у многих проводников холловский потенциал положителен. Это Be, Zn, Cd, Tl, V, Cr, Fe, Co, Pb, Mo, Ru, As, Sb, Ta, W, Re, Ir. Многие из этих проводников по химическим свойствам типичные металлы. Формально получается, что носителями тока в этих проводниках являются положительно заряженные частицы. Этот факт не мог быть объяснён в рамках классической электронной теории проводимости металлов. И лишь с развитием квантовой теории проводимости стало ясно, что в проводниках второй группы преобладают дырочные носители тока. Заряд переносится электронами не в зоне проводимости, а в валентной зоне.

Из формулы (15.2) можно найти концентрацию n носителей тока в проводнике. Если разделить число n на количество атомов N в единице объёма проводника, N = rN_AçM, где r - плотность вещества проводника, M- его молярная (атомная) масса, N_A - число Авогадро, то получаем число носителей тока, приходящихся в среднем на один атом проводника.

Таблица 15.1
Проводник	Na	Ag	Al	Ni
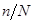
	1,16	1,49	0,417	0,130

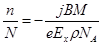. (15.3)

В таблице 15.1 приведены значения отношений 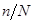для некоторых проводников.

5. Циклотронный резонанс. Суть его в том, что электромагнитная волна, падая на образец, помещённый в постоянное магнитное поле B, при некотором соотношении между индукцией B и частотой волны w интенсивно поглощается.

Предположим, что на плоской плёночный образец О, расположенный между полюсами электромагнита перпендикулярно линиям B, падает электромагнитная волна. Излучатель волны И ориентирован так, что вектор E колеблется параллельно плоскости образца вдоль оси ОХ (рис.106).

Отражённая от образца волна попадает в приёмник П, измеряющий её интенсивность I_отр. При изменении частоты волны w при некотором её значении w = w _р наблюдается резкое уменьшение коэффициента отражения R = I_отрçI_пад (рис.107).

В первом приближении эффект хорошо объясняется в рамках модели свободных электронов проводимости, не соударяющихся с узлами кристаллической решётки проводника. В тот момент, когда частота изменения электрического поля волны 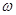будет приближаться к циклотронной частоте носителей заряда w _р = B(eçm) (См. формулу 14.15), носители тока в проводнике будут разгоняться по спирали (рис.106). Их кинетическая энергия будет расти за счёт энергии волны. Поэтому интенсивность отражённой волны при резонансе уменьшается.

Обычно изменяют не частоту w волны, излучаемой генератором, а индукцию поля B, создаваемого электромагнитом, что значительно проще.

Циклотронный резонанс проявляется во всех проводниках – твёрдых, жидких и газообразных. Он широко используется для измерения удельного заряда носителей тока в разных средах.

Для проводников, где носителями тока являются электроны проводимости, резонансные частоты соответствуют волнам сантиметрового диапазона. Так как индукция магнитного поля B обычно около 0,1 Тл, то w _р = B(eçm) = 0,1×1,6×10¹¹=1,6×10¹⁰ c^-1. Отсюда длина волны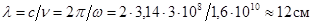

Измерение удельного заряда eçm методом циклотронного резонанса в твёрдых проводниках показало, что величина eçm электронов проводимости в кристаллах отличается от удельного заряда eçm свободных электронов в вакууме. Это можно объяснить лишь взаимодействием электронов с полем кристаллической решётки проводника. Поэтому удельный заряд электронов проводимости трактуется как отношение eçm_эф, где m_эф - так называемая эффективная масса электрона проводимости в данном кристалле.

В монокристаллах эффективная масса электронов проводимости зависит от ориентации направления силы eE (ось ОХ на рис.106) относительно кристаллографических осей. По разным направлениям отношение m_эфçm может быть как больше, так и меньше 1.

Здесь m- масса свободного электрона в вакууме, m = 9,1×10^-31 кг.

6.Циклотроны – ускорители заряженных частиц. Действие циклотронов основано на независимости периода обращения частиц в магнитном поле от их энергии. В циклотронах ускоряются тяжёлые частицы – ионы без применения высокого напряжения.

Идею циклотрона – магнитного резонансного ускорителя выдвинул в 1929 г. американец Эрнест Лоуренс. Под его руководством были построены первые циклотроны, положившие начало циклическим ускорителям.

Конструктивно циклотрон состоит из двух дуантов – половинок полой цилиндрической коробки, помещённых в магнитное поле электромагнита (рис.108). Между дуантами имеется щель шириной l. К дуантам приложено переменное электрическое напряжение несколько десятков киловольт, создаваемое специальным высокочастот-ным генератором. Поэтому в щели между дуантами существует электрическое поле, способное ускорять ионы. Магнитное поле на рис.108 перпендикулярно плоскости рисунка.

В источнике И ионы создаются в газовом разряде низкого давления. Имея энергию несколько килоэлектронвольт, они вводятся в пространство циклотрона в центре щели между дуантами. В камере циклотрона вакуум. Поэтому ионы в щели ускоряются электрическим полем и к моменту выхода из щели в полость дуанта, где электрического поля нет, приобретают некоторую скорость движения. Внутри дуанта ион движется по инерции по дуге ларморовой окружности. За время движения иона в дуанте поле в щели меняет знак. Поэтому проходя щель, ион вновь ускоряется.

Поскольку циклотронная частота обращения частиц при v << c не зависит от скорости v, w = B(eçm), то моменты прохождения частиц через щель следуют через равные промежутки времени. Поэтому генератор переменного напряжения может работать с постоянной частотой. Частицы движутся в циклотроне по плоской развёртывающейся спирали. На последнем витке спирали включается отклоняющее электрическое поле, которое выводит пучок наружу.

Максимальная энергия частиц при выходе из циклотрона не зависит от ускоряющего электрического поля. Она определяется индукцией магнитного поля B и радиусом R последнего витка спирали. Действительно скорость, приобретаемая частицей на последнем витке, v = wR, а её кинетическая энергия 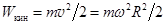. Подставив сюда значение w из формулы (14.5), w = B(eçm), получаем: 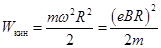. (15.4)

Индукция B в циклотронах достигает 1 Тл. Диаметр последнего витка спирали около1 м, R = 0,5 м, При ускорении ионов водорода (протоны) их максимальная энергия может достигать 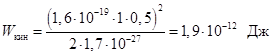или, разделив на 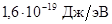, получаем в электронвольтах: W_кин = 12 МэВ. Предел ускорения частиц в циклотроне кладёт зависимость их массы от скорости. Когда скорость частиц становится заметной по сравнению со скоростью света, их масса увеличивается, а циклотронная частота уменьшается. Поскольку генератор работает с постоянной частотой, то частица выходит из резонанса, её ускорение прекращается.

В более поздних модификациях циклотронов эта проблема решается по-разному. В фазотронах магнитное поле постоянно, а частота ускоряющего электрического поля уменьшается. Верхняя граница для протонов поднимается в них до 100 МэВ.

В синхротронах, применяемых для ускорения электронов, изменяется во времени магнитное поле, а частота генератора остаётся постоянной. Энергия ускоренных электронов достигает 10 ГэВ.

В синхрофазотронах изменяются во времени и частота генератора, и магнитное поле. Энергия протонов здесь может достигать 1000 ГэВ.