Индукция магнитного поля, образованного плоским тонким круговым контуром с током, в произвольной точке пространства.
 Пусть по тонкому плоскому круговому кольцу, расположенному в плоскости z=0, с центром в начале координат x = 0, y = 0 течёт ток
Пусть по тонкому плоскому круговому кольцу, расположенному в плоскости z=0, с центром в начале координат x = 0, y = 0 течёт ток 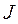 . Пусть радиус проводящего кольца равен
. Пусть радиус проводящего кольца равен 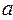 . Пусть точка наблюдения М вектора магнитной индукции
. Пусть точка наблюдения М вектора магнитной индукции  определена радиус-вектором
определена радиус-вектором 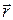 с компонентами
с компонентами 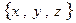 .
.
Компоненты радиус-вектора 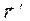 расположения элемента контура с током удобно описать параметрически:
расположения элемента контура с током удобно описать параметрически:
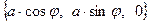 , где
, где 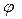 - угол между направлением на рассматриваемый элемент и положительным направлением оси абсцисс. Допустим, что электрический ток течёт вдоль контура против часовой стрелки, если учесть положительное направление оси аппликат. В этом случае вектор
- угол между направлением на рассматриваемый элемент и положительным направлением оси абсцисс. Допустим, что электрический ток течёт вдоль контура против часовой стрелки, если учесть положительное направление оси аппликат. В этом случае вектор 
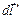 имеет следующие составляющие:
имеет следующие составляющие:
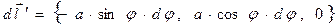 . (1)
. (1)
Разность радиус-векторов точки наблюдения и точки расположения элемента контура с током описывается выражением:
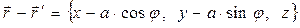 . (2)
. (2)
Модуль выражения (2) имеет вид:
 . (3)
. (3)
Векторное произведение в числителе выражения (1) раздела 6.2 принимает форму: 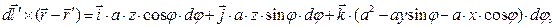
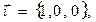
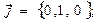
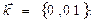 (4)
(4)
Запишем координатную форму соотношения (1)раздела 6.2 для рассматриваемого случая:
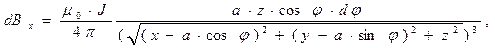 (5)
(5)
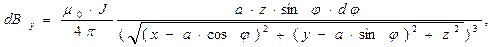 (6)
(6)
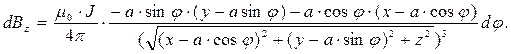 (7)
(7)
В соответствии с принципом суперпозиции (3) раздела 6.2 для расчёта компонент вектора магнитной индукции в точке наблюдения необходимо проинтегрировать выражения (5)-(7) по переменной 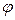 в пределах от 0 до
в пределах от 0 до 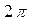 :
:
 (8)
(8)
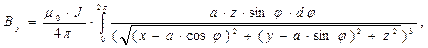 (9)
(9)
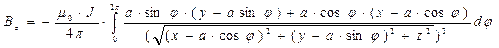 , (10)
, (10)
В выражениях (8)-(10) произвольные значения координат точки наблюдения x,y,z играют роль параметров.
Наиболее простые и наглядные результаты получаются для точки наблюдения, расположенной на оси аппликат (x = 0, y = 0, z - произвольное значение):

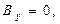
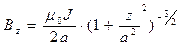 . (11)
. (11)
В центре проводящего кругового кольца проекция вектора магнитной индукции на ось аппликат принимает значение:
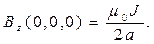 (12)
(12)
Эти результаты были получены выше (соотношения (3)-(4) предыдущего раздела) при рассмотрении частного случая задачи.
Введём в рассмотрение безразмерный (относительный) вектор 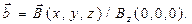 С помощью выражений (8)-(10) рассчитаем проекции вектора
С помощью выражений (8)-(10) рассчитаем проекции вектора 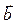 в некоторых характерных точках пространства. Так для точки наблюдения с декартовыми координатами {
в некоторых характерных точках пространства. Так для точки наблюдения с декартовыми координатами { 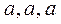 } получаем результаты: bx = 0.0496, by = 0.0496, bz = 0.0212. Для точки наблюдения «повыше» (координаты {
} получаем результаты: bx = 0.0496, by = 0.0496, bz = 0.0212. Для точки наблюдения «повыше» (координаты { 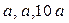 }) соответственно получаем: bx = 6.972×10-5, by =6.972×10-5 , bz = 4.647×10-4. Компоненты уменьшились по величине, появились проекции на оси абсцисс и ординат.
}) соответственно получаем: bx = 6.972×10-5, by =6.972×10-5 , bz = 4.647×10-4. Компоненты уменьшились по величине, появились проекции на оси абсцисс и ординат.
Если воспользоваться тем, что рассматриваемая система токов обладает осевой симметрией, можно систему координат расположить специальным образом: пусть точка наблюдения M расположена в плоскости y=0. С помощью компьютерной системы символьных вычислений Mapleможно получить аналитические зависимости для расчёта выражений (8)-(10) как функций координат x и z:
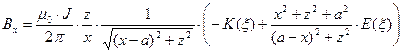 ,
, 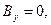
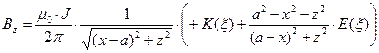 , (13)
, (13)
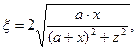
 ,
, 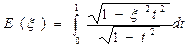 .
.
В соотношениях (13) 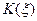 и
и 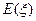 - полные эллиптические интегралы первого и второго рода соответственно.
- полные эллиптические интегралы первого и второго рода соответственно.
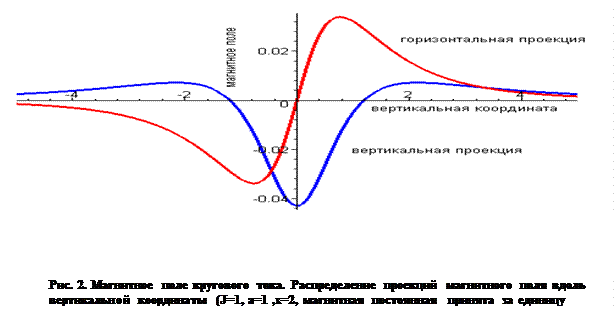
С помощью полученных выражений несложно рассчитать составляющие вектора магнитной индукции при переходе в произвольную систему координат. На рис. 2 показаны результаты расчета горизонтальной и вертикальной составляющих вектора магнитной индукции кругового кольца с током в зависимости от вертикальной координаты точки наблюдения (горизонтальная координата точки наблюдения была фиксирована).
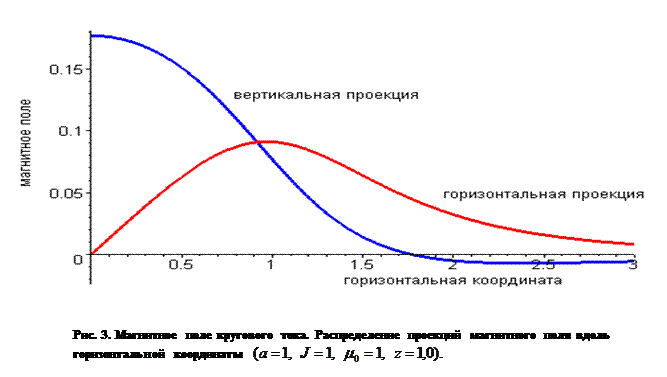
На рис. 3 приведены аналогичные результаты расчетов составляющих вектора магнитной индукции поля кругового кольца с током в зависимости от горизонтальной координаты х (вертикальная координата точки наблюдения фиксирована).
Дата добавления: 2017-09-01; просмотров: 1475;











