Модель экстраполятора 0-го порядка

Экстраполятор нулевого порядка производит дискретизацию входного сигнала с периодом квантования h (Рис. 2.5).

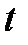
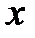
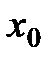
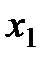
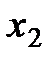
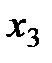
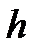
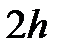
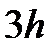
Рис. 2.5 Работа экстраполятора 0-ого порядка

Его реализация основана на планировании дискретных событий в моменты времени кратные периоду квантования 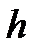. При возникновении данного события вычислительная процедура блока сохраняет текущее значение на входе и генерирует его на выход до появления следующего аналогичного события.

Оптимизация

Оптимизация динамических систем является важной частью моделирующих программ, и ее реализация позволяет значительно увеличить полезность разрабатываемого инструментария.

Оптимизация динамической системы подразумевает нахождение таких ее параметров, которые минимизируют (максимизируют) определенные динамические свойства или характеристики системы. Примером оптимизации динамической системы является нахождение оптимальных настроек регулятора САР, которые позволяют достигнуть наилучшего качества переходного процесса (перерегулирование, время регулирования и т. д.)

В общем случае постановка задачи оптимизации содержит:

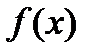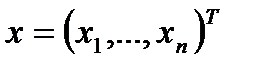· Целевую функцию , где , определенную на n-мерном евклидовом пространстве 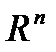. Ее значения характеризуют степень достижения цели, во имя которой поставлена и решается задача;

· Множество допустимых решений 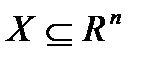, среди элементов которого осуществляется поиск.

Требуется найти такой вектор 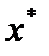из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве:

.

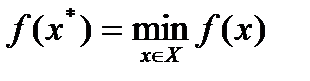Задача поиска максимума функции 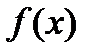сводится к задаче поиска минимума путем замены знака перед функцией на противоположный:

.

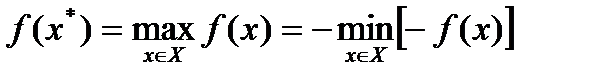Задача поиска минимума и максимума целевой функции 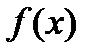называется задачей поиска экстремума:

.

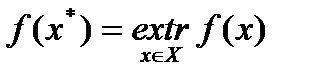Точка 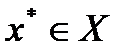называется точкой глобального минимума функции 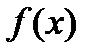на множестве 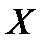, если функция достигает в этой точке своего наименьшего значения, т.е.

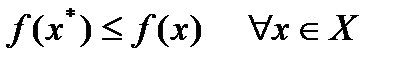. (2.35)

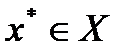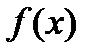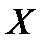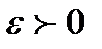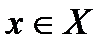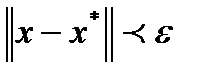Точка называется точкой локального минимума функции на множестве , если существует , такое, что если и , то 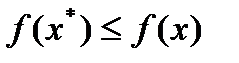. Здесь 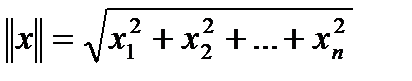- эвклидова норма вектора .

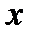Если множество допустимых решений 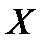задается ограничениями (условиями), накладываемыми на вектор 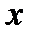, то решается задача поиска условного экстремума (условная оптимизация).

Если 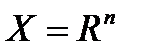, т.е. ограничения на вектор 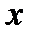отсутствуют, решается задача поиска безусловного экстремума (безусловная оптимизация).

Для решения задачи поиска экстремума функции используются различные методы оптимизации, которые будут рассмотрены в следующих разделах.