Методы безусловной оптимизации
Возможны два подхода к решению задачи отыскания минимума функции многих переменных 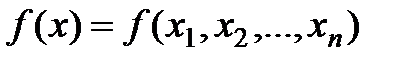 при отсутствии ограничений на диапазон изменения неизвестных.
при отсутствии ограничений на диапазон изменения неизвестных.
Первый подход лежит в основе косвенных методов оптимизации и сводит решение задачи оптимизации к решению системы нелинейных уравнений, являющихся следствием условий экстремума функции многих переменных. Как известно, эти условия определяют, что в точке экстремума х* все первые производные функции по независимым переменным равны нулю:
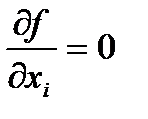 , при
, при 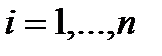 .
.
Эти условия образуют систему n нелинейных уравнений, среди решений которой находятся точки минимума. Вектор 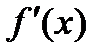 , составленный из первых производных функции по каждой переменной, т.е.
, составленный из первых производных функции по каждой переменной, т.е.
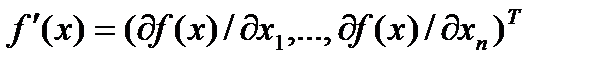
называют градиентом скалярной функции 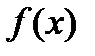 . Как видно, в точке минимума градиент равен нулю.
. Как видно, в точке минимума градиент равен нулю.
Решение систем нелинейных уравнений - задача весьма сложная и трудоемкая. Вследствие этого на практике используют второй подход к минимизации функций, составляющий основу прямых методов. Суть их состоит в построении последовательности векторов 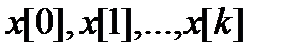 , таких, что
, таких, что 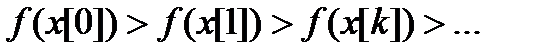 . В качестве начальной точки
. В качестве начальной точки 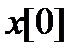 может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции
может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции 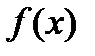 , чтобы точка
, чтобы точка 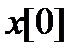 располагалась как можно ближе к точке минимума. Переход (итерация) от точки
располагалась как можно ближе к точке минимума. Переход (итерация) от точки 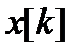 к точке
к точке 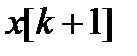 ,
, 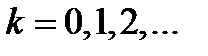 , состоит из двух этапов:
, состоит из двух этапов:
1) выбор направления движения из точки 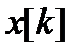 ;
;
2) определение шага вдоль этого направления.
Методы построения таких последовательностей часто называют методами спуска, так как осуществляется переход от больших значений функций к меньшим значениям.
Математически методы спуска описываются соотношением
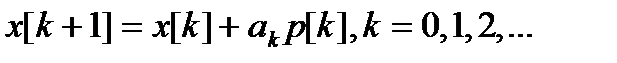 (2.36)
(2.36)
где 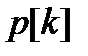 - вектор, определяющий направление спуска;
- вектор, определяющий направление спуска; 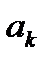 - длина шага.
- длина шага.
Различные методы спуска отличаются друг от друга способами выбора двух параметров - направления спуска и длины шага вдоль этого направления. На практике применяются только методы, обладающие сходимостью. Они позволяют за конечное число шагов получить точку минимума или подойти к точке, достаточно близкой к точке минимума. Качество сходящихся итерационных методов оценивают по скорости сходимости.
В методах спуска решение задачи теоретически получается за бесконечное число итераций. На практике вычисления прекращаются при выполнении некоторых критериев (условий) останова итерационного процесса. Например, это может быть условие малости приращения аргумента
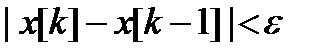 (2.37)
(2.37)
или функции
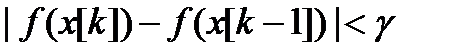 , (2.38)
, (2.38)
где k - номер итерации;
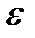 ,
, 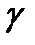 - заданные величины точности решения задачи.
- заданные величины точности решения задачи.
Методы поиска точки минимума называются детерминированными, если оба элемента перехода от 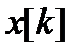 к
к 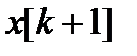 (направление движения и величина шага) выбираются однозначно по доступной в точке
(направление движения и величина шага) выбираются однозначно по доступной в точке 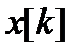 информации. Если же при переходе используется какой-либо случайный механизм, то алгоритм поиска называется случайным поиском минимума.
информации. Если же при переходе используется какой-либо случайный механизм, то алгоритм поиска называется случайным поиском минимума.
Детерминированные алгоритмы безусловной минимизации делят на классы в зависимости от вида используемой информации. Если на каждой итерации используются лишь значения минимизируемых функций, то метод называется методом нулевого порядка. Если, кроме того, требуется вычисление первых производных минимизируемой функции, то имеют место методы первого порядка, при необходимости дополнительного вычисления вторых производных - методы второго порядка.
В настоящее время разработано множество численных методов для задач как безусловной, так и условной оптимизации. Естественным является стремление выбрать для решения конкретной задачи наилучший метод, позволяющий за наименьшее время использования ЭВМ получить решение с заданной точностью.
Качество численного метода характеризуется многими факторами: скоростью сходимости, временем выполнения одной итерации, объемом памяти ЭВМ, необходимым для реализации метода, классом решаемых задач и т. д.
Для организации подсистемы оптимизации в разрабатываемой системе необходимо выбрать методы для реализации, исходя из типа решаемой задачи и качества метода. Специфика оптимизации динамических систем, заданных структурными схемами и неявность задания целевой функции, значение которой может быть рассчитано только после проведения моделирования всей системы в целом обуславливают использования методов нулевого порядка.
В этих методах для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации в данном случае полностью определяется последовательными вычислениями значений функции. Следует отметить, что при решении задач безусловной минимизации методы первого и второго порядков обладают, как правило, более высокой скоростью сходимости, чем методы нулевого порядка. Однако на практике вычисление первых и вторых производных функции большого количества переменных весьма трудоемко. В ряде случаев они не могут быть получены в виде аналитических функций. Определение производных с помощью различных численных методов осуществляется с ошибками, которые могут ограничить применение таких методов. Кроме того, на практике встречаются задачи, решение которых возможно лишь с помощью методов нулевого порядка, например задачи минимизации функций с разрывными первыми производными. Критерий оптимальности может быть задан не в явном виде, а системой уравнений. В этом случае аналитическое или численное определение производных становится очень сложным, а иногда невозможным. Для решения таких практических задач оптимизации могут быть успешно применены методы нулевого порядка.
В разрабатываемой системе были реализованы 2 метода оптимизации нулевого порядка: метод Хука-Дживса и метод Нелдера-Мида. Выбор данных методов обусловлен:
1) их хорошей алгоритмизацией, легкостью реализации;
2) удобством модификации методов для реализации условной оптимизации;
3) наличием тестовых примеров для отладки.
Необходимость реализации как минимум двух методов вытекает из разнообразия решаемых задач: они могут иметь высокую и малую размерность, быть унимодальными (обладающими одним экстремумом) и многоэкстремальными и т. д. В ситуации, когда один метод плохо сходится или вообще не может найти оптимального решения, другой метод может дать положительный результат. Очевидно, что разумное сочетание разнообразных методов, учет их свойств позволят с наибольшей эффективностью решать поставленные задачи и такой многометодный способ решения весьма удобен в диалоговом режиме работы системой моделирования.
Метод Хука-Дживса
Суть этого метода состоит в следующем. Задаются некоторой начальной точкой 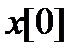 . Изменяя компоненты вектора
. Изменяя компоненты вектора 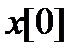 , обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции
, обследуют окрестность данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции 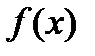 . В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
. В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.
Исходными данными для работы метода являются:
1) 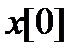 – вектор начальных значений;
– вектор начальных значений;
2) d – начальный шаг поиска;
3) 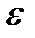 – минимальный шаг поиска.
– минимальный шаг поиска.
Ниже представлена блок-схема алгоритма метода Хука-Дживса.
| Нет |
| Да |
| Да |
| Нет |
| h < e |
| h = h / 5 |
| fk < fb |
| Исследование в точке xb (шаг h): xk, fk = f(xk) |
| xb=x[0] fb = f(xb) |
| Ввод x[0], d, e |
| Начало |
| xb = xk h = h / 5 |
| Нет |
| xb = xk2 xk = xk3 fb = fk = xk3 |
| Да |
| xk3 < xk2 |
| Выход |
| Вывод xb |
| xb = xk |
| Исследование в точке xk2 (шаг h): xk3, fk3 = f(xk3) |
| xk2 = 2xk-xb fk2 = f(xk2) |
Рис. 2.6 Блок-схема алгоритма метода Хука-Дживса
Заметим, что величина уменьшение шага в 5 раз выбрана экспериментальным путем, ее изменение может привести к увеличению или уменьшению скорости сходимости метода в зависимости от решаемой задачи.
Метод Нелдера-Мида
Данный метод состоит в том, что для минимизации функции n переменных 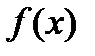 в n-мерном пространстве строится многогранник, содержащий (n + 1) вершину. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции
в n-мерном пространстве строится многогранник, содержащий (n + 1) вершину. Очевидно, что каждая вершина соответствует некоторому вектору х. Вычисляются значения целевой функции 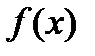 в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина
в каждой из вершин многогранника, определяются максимальное из этих значений и соответствующая ему вершина 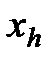 , минимальное (вершина
, минимальное (вершина 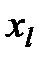 ) и значение следующее за наибольшим (вершина
) и значение следующее за наибольшим (вершина 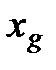 ). Через
). Через 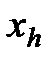 и центр тяжести остальных вершин
и центр тяжести остальных вершин 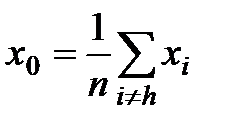 проводится проецирующая прямая, на которой находится точка с меньшим значением целевой функции, чем в вершине
проводится проецирующая прямая, на которой находится точка с меньшим значением целевой функции, чем в вершине 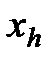 . Затем из многогранника исключается вершина
. Затем из многогранника исключается вершина 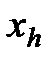 . Из оставшихся вершин и полученной точки строится новый многогранник, с которым повторяется описанная процедура.
. Из оставшихся вершин и полученной точки строится новый многогранник, с которым повторяется описанная процедура.
В процессе выполнения данных операций многогранник изменяет свои размеры и форму в соответствии с тремя операциями: отражение, растяжение, сжатие.
Точку 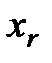 расчитывают как отражение
расчитывают как отражение 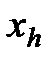 относительно
относительно 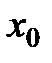 :
:
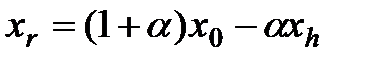 ,
,
где 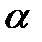 – коэффициент отражение. Обычно
– коэффициент отражение. Обычно 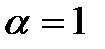 .
.
Точку 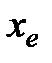 расчитывают как растяжение
расчитывают как растяжение 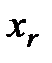 относительно
относительно 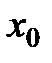 :
:
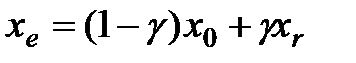 ,
,
где 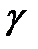 – коэффициент растяжения. Обычно
– коэффициент растяжения. Обычно 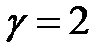 .
.
Точку 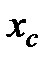 расчитывают сжатие
расчитывают сжатие 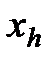 относительно
относительно 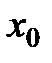 :
:
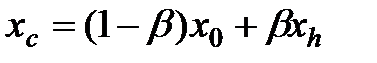 ,
,
где 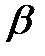 – коэффициент сжатия. Обычно
– коэффициент сжатия. Обычно 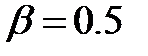 .
.
При невозможности получить уменьшения значения функции симплекс сжимается в 2 раза вокруг точки 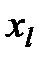 по формуле:
по формуле:
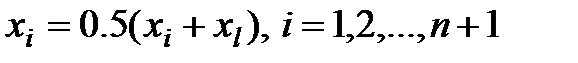
Проверка сходимости метода использует не разницу между значениями фукнций 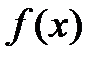 или векторов
или векторов 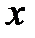 на соседних итерациях, а стандартное отклонение значений функций в вершинах симплекса (многогранника):
на соседних итерациях, а стандартное отклонение значений функций в вершинах симплекса (многогранника):
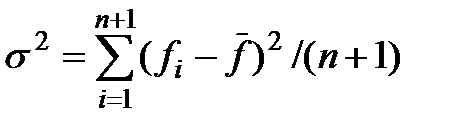 , где
, где 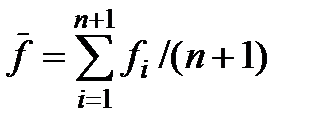 .
.
Считается, что работа метода завершена при  , где
, где 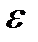 – минимальное стандартное отклонение метода.
– минимальное стандартное отклонение метода.
Блок-схема работы алгоритма Нелдера-Мида представлена на рис. 2.7
| Да |
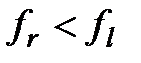
|
Найти 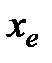 , , 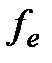
|
| Да |
| Нет |
| Нет |
| Да |
| Да |
| Нет |
| Да |
| Нет |
| Нет |
| Да |
| Нет |
Заменить
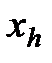 на на 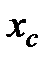
|
Заменить
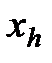 на на 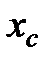
|
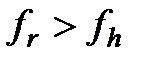
|
Найти 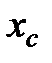 , , 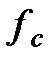
|
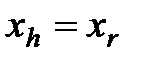
|
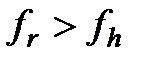
|
Заменить 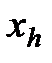 на на 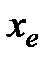
|
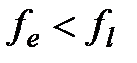
|
| Конец |
| Проверка сходимости |
Рассчет 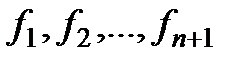
|
Заменить 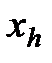 на на 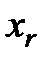
|
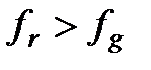
|
Найти 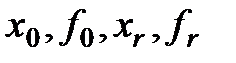
|
Найти
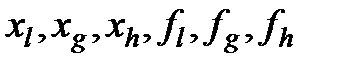
|
Рассчет
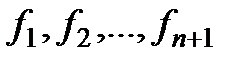
|
Ввод x[0], 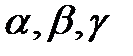 , e , e
|
| Начало |
Рис. 2.7 Блок-схема алгоритма метода Нелдера-Мида
Дата добавления: 2021-10-28; просмотров: 468;











