Условная оптимизация

В реальных условиях на переменные 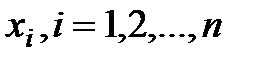, и некоторые функции 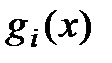, , 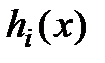характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:

;

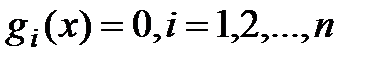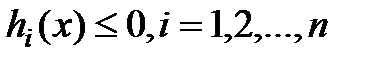; (2.39)

.

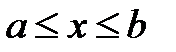Такую задачу называют задачей условной оптимизации.

Каждая точка х в n-мерном пространстве переменных 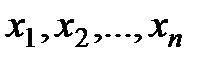, в которой выполняются ограничения, называется допустимой точкой задачи. Множество всех допустимых точек называют допустимой областью G. Решением задачи (оптимальной точкой) называют допустимую точку х*, в которой целевая функция 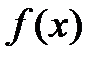достигает своего минимального значения.

В разработанной системе моделирования реализованна условная оптимизация с ограничениями только одного вида: .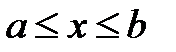

Решение поставленной задачи может быть достигнуто двумя способами:

1) Прямая проверка ограничений. Данный метод наиболее прост в реализации. Для этого необходимо при решении задачи оптимизации присвоить целевой функции очень большое значение там, где ограничения нарушаются. График зависимости целевой функции одной переменной 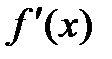при использовании данного метода показан на рис. 2.8.

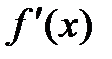
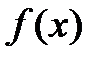
b

a

Очень большое значение

Рис. 2.8. Ограничение типа «обрыв»

Данный подход обладает одним недостатком: метод не может двигаться вдоль границы области ограничений и сходимость достигается в первой же точке границы, где и находится решение. Поэтому зачастую для нахождения правильного решения требуются более изощренные процедуры, чем приведенная выше.

Использование штрафных функций. Основная идея метода состоит в преобразовании задачи минимизации функции 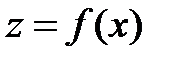с ограничениями, наложенными на 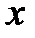, в задачу поиска минимума без ограничений функции

,

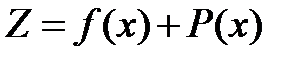где 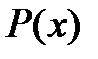– штрафная функция.

Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию 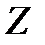, т. е. увеличивала ее значение. В этом случае минимум 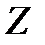будет находиться внутри области ограничений.

Для ограничения 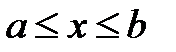штрафная функция может быть представлена в следующем виде:

,

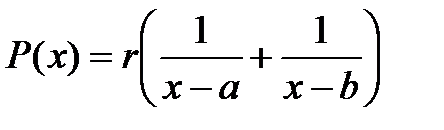где 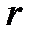– значение, определяющее крутизну ограничивающих кривых. Обычно .

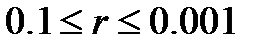График зависимости целевой функции одной переменной 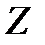при использовании данного метода показан на рис. 2.9.

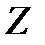
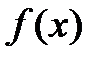
b

a

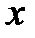
Рис. 2.9. Ограничение с использованием штрафных функций