Нахождение глобального минимума целевой функции

Целью оптимизации динамической системы является нахождения глобального экстремума целевой функции, т. е. определения таких значений оптимизируемых параметров в их областях допустимых значений, которые дадут наилучший результат целевой функции. На практике рассматриваемые методы не способны обеспечить стопроцентное нахождение глобального минимума. Зачастую они сходятся к локальному минимуму функции ( 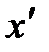), а точка глобального минимума ( 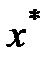) остается за пределами исследований метода (рис 2.10).

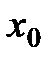
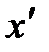
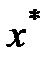
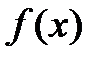
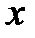
Рис. 2.10. Нахождение локального минимума методами прямого поиска

Появление данной ситуация зависит от многих факторов. Перечислим некоторые из них:

1) вид зависимости целевой функции от оптимизируемых параметров;

2) величина начального шага поиска метода;

3) положение начальной точки.

Так как зависимость целевой функции от параметров динамической системы носит обычно сложный характер и выражена неявно, то попытка увеличить вероятность нахождения глобального минимума может быть реализована через изменения алгоритмом моделирования факторов 2 и 3.

Рассмотрим алгоритм нахождения глобального минимума на основе изменения оптимизирующим методом начальной точки. Вначале определяется область возможных значений для оптимизируемых параметров. Если на некоторый параметр не наложено ограничение вида 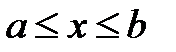, то границы его изменения определяются исходя из настроек метода.

В общем случае существует 2 метода изменения начальной точки поиска (рис 2.11.):

· сеточный – начальными точками являются значения в каждом узле сетки параметра, сформированной с определенным шагом;

· стохастический – начальными точками являются случайные значения параметров из области возможных значений;

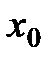
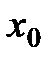
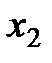
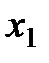
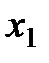
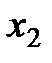
а) б)

Рис. 2.11. Метод изменения начальной точки поиска для функции 2-х параметров: а) – сеточный, б) - стохастический

Теперь рассмотрим сам алгоритм нахождения глобального минимума, использующий стохастический метод выбора начальных точек (рис. 2.12)

Нет

Начало

Конец

Проведено достаточно циклов

Да

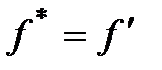
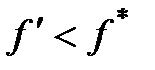
Проведение оптимизации одним из описанных методов с начальной точкой 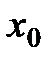: 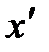- локальный минимум

Определение начальной точки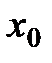

Рис. 2.12 Блок-схема алгоритма нахождения глобального минимума

Еще раз следует отменить, что использование данного метода не может гарантировать нахождение глобального минимума, но существенно увеличивает данную вероятность.