Трехфазные цепи типа «звезда-звезда»
В качестве первого примера рассматривается цепь с идеальными источниками ЭДС при отсутствии сопротивлений в линейных проводах (рис. 16).
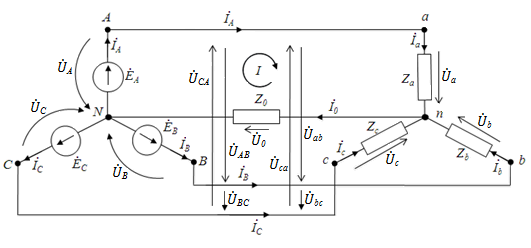
Рис. 16
Понятно, что оптимальным для такой цепи методом расчета является метод двух узлов, в соответствии с которым напряжение между узлами «n» и «N», т.е. смещение нейтралей, равно:
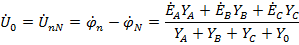
В соответствии со вторым законом Кирхгофа для первого контура получаем:
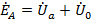 или
или 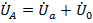 , т.е.
, т.е. 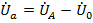 .
.
Таким образом, фазное напряжение на нагрузке отличается от соответствующего фазного напряжения на генераторе на величину смещения нейтрали.
Аналогично:
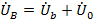 →
→ 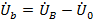 и
и
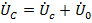 →
→ 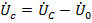 …
…
Эти соотношения чрезвычайно просты и легки для запоминания.
По известным фазным напряжениям на нагрузке легко находятся фазные токи
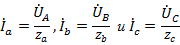 .
.
Что касается тока в нулевом проводе, то на основании закона Ома и первого закона Кирхгофа 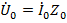 и
и 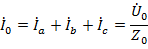
Понятно, что токи в линейных проводах 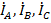 и фазах, как генератора, так и нагрузки при соединении фаз по схеме «звезда» - это одни и те же токи:
и фазах, как генератора, так и нагрузки при соединении фаз по схеме «звезда» - это одни и те же токи: 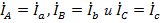 .
.
В связи с симметрией ЭДС фаз на стороне генератора векторная диаграмма напряжений на его зажимах представляет из себя, как было показано, равносторонний треугольник ABC линейных напряжений 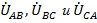 и равновеликую трехлучевую звезду
и равновеликую трехлучевую звезду 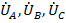 , исходящую из нейтрали «N» - фазных.
, исходящую из нейтрали «N» - фазных.
Поскольку при отсутствии сопротивлений в линейных проводах падения напряжения между началами фаз генератора /A; B; C/ и нагрузки /a, b, c/ отсутствуют, потенциалы точек A и a, B и b, C и c совпадают, т.е. 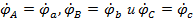 . Следовательно, точки A и a, B и b, C и c на векторной диаграмме совмещены (смещение начал фаз отсутствует), т.е.
. Следовательно, точки A и a, B и b, C и c на векторной диаграмме совмещены (смещение начал фаз отсутствует), т.е. 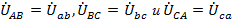 (рис. 17).
(рис. 17).
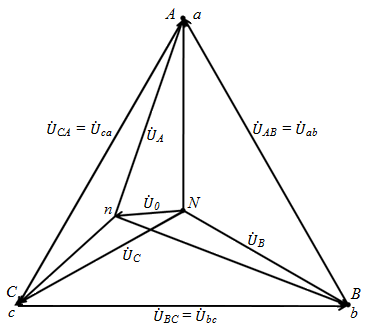
Рис. 17
Что касается фазных напряжений на нагрузке, то смещение нейтрали искажает их симметрию.
В общем случае точка «n» может занять любое положение внутри треугольника, а теоретически даже вне его, но с соблюдением обязательных соотношений 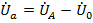 ,
, 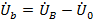 и
и 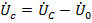 .
.
Дата добавления: 2018-05-10; просмотров: 1498;











