Фазные напряжения на нагрузке представляются в этом случае произвольной трехлучевой звездой, исходящей из точки «n».
Искажение напряжений на фазах нагрузки крайне нежелательно. Оно снижает качество потребляемой энергии, отрицательно сказываясь на работе не только включенных в отдельные фазы однофазных приёмников, например, отдельных квартир многоквартирных домов, но к заметному снижению эффективности работы собственно трехфазных приемников (например, трехфазных синхронных или асинхронных двигателей).
Все это заставляет эксплуатирующих трехфазные системы электроэнергетиков искать средства уменьшения, а в идеале исключения смещения нейтрали.
Анализ выражений для 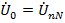 показывает две возможности для этого.
показывает две возможности для этого.
Главной из них является необходимость приведения реальных трехфазных нагрузок к симметричным, ибо при 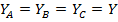 смещение нейтрали становится равным
смещение нейтрали становится равным
 0=
0= 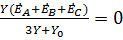 , поскольку в условиях симметричных систем ЭДС
, поскольку в условиях симметричных систем ЭДС 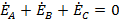 .
. 
Конечно, добиться идеальной симметрии нагрузки при наличии однофазных потребителей практически невозможно. Некоторая несимметрия все-таки будет иметь место, что будет приводить хотя и к не очень значительному, но все таки смещению нейтрали.
В этой связи свою, по сути, основную роль начинает играть собственно нулевой провод, присутствие которого в цепи приводит к уменьшению величины 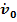 и к уменьшению искажения фазных напряжений. И уравнение для двух узлов, и
и к уменьшению искажения фазных напряжений. И уравнение для двух узлов, и 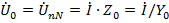 показывают, что присутствие
показывают, что присутствие 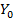 оказывает заметное влияние на величину
оказывает заметное влияние на величину 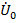 .
.
В то же время, поскольку 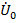 не приобретает больших значений, величина тока нулевого провода /
не приобретает больших значений, величина тока нулевого провода / 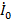 / существенно меньше линейных токов. В этой связи сечение нулевого провода, как правило, меньше сечения линейных проводов, что позволяет определить его в составе и воздушной, и кабельной четырехпроводной сети.
/ существенно меньше линейных токов. В этой связи сечение нулевого провода, как правило, меньше сечения линейных проводов, что позволяет определить его в составе и воздушной, и кабельной четырехпроводной сети.
Векторная диаграмма токов для несимметричной нагрузки с учетом первого закона Кирхгофа для узла «n» 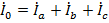 представлена на рис. 18.
представлена на рис. 18.
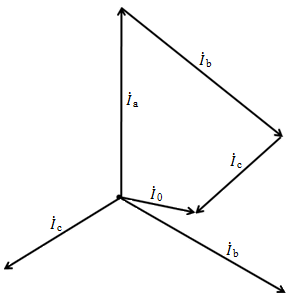
Рис. 18.
Понятно, что эта векторная диаграмма построена произвольно.
При совмещении векторной диаграммы токов с диаграммой напряжений следует учитывать, как было отмечено ранее, сдвиг по фазе между каждым фазным током и соответствующим фазным напряжением 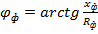 . Это относится и к току нулевого провода
. Это относится и к току нулевого провода 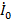 с падением напряжения
с падением напряжения 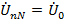 .
.
При симметричной нагрузке 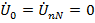 , точка «n» совмещается с «N», фазные напряжения на нагрузке становится равным фазным напряжениям на стороне генератора
, точка «n» совмещается с «N», фазные напряжения на нагрузке становится равным фазным напряжениям на стороне генератора 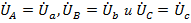 вместе образуя равновеликую трехлучевую звезду. Ток в нулевом проводе при этом
вместе образуя равновеликую трехлучевую звезду. Ток в нулевом проводе при этом 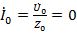 отсутствует, надобность в нем отпадает, т.к. в этом случае
отсутствует, надобность в нем отпадает, т.к. в этом случае 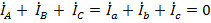 . На векторной диаграмме фазные токи представляют равновеликую трехлучевую звезду.
. На векторной диаграмме фазные токи представляют равновеликую трехлучевую звезду.
Если при малых значениях сопротивления 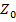 им можно пренебречь, посчитав
им можно пренебречь, посчитав 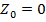 , симметрия фазных напряжений на нагрузке и их равенство фазным напряжениям на генераторе будет обеспечиваться при любой нагрузке. Токи в фазах при этом будут, естественно, разными.
, симметрия фазных напряжений на нагрузке и их равенство фазным напряжениям на генераторе будет обеспечиваться при любой нагрузке. Токи в фазах при этом будут, естественно, разными.
Отсутствие сопротивлений в линейных проводах схем трехфазных энергетических систем вполне оправдано в тех случаях, когда удаление нагрузки от источника питания незначительно, например, когда питание осуществляется от местной трансформаторной подстанции.
В других случаях учет этих сопротивлений необходим. Никаких принципиальных изменений в расчет цепи сопротивления линейных проводов не привносят, изменяя лишь сопротивления каждой фазы.
Понятно, что сопротивления всех трех линейных проводов одинаковы 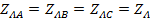 и симметрии нагрузки они не нарушают. В каждом линейном проводе падения напряжения формируются соответствующими линейными токами, так что
и симметрии нагрузки они не нарушают. В каждом линейном проводе падения напряжения формируются соответствующими линейными токами, так что 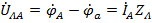 ,
, 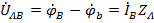 ,
, 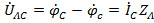 .
.
Поскольку сопротивления линейных проводов носят индуктивный характер (ёмкостная составляющая ничтожна), 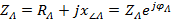 . Таким образом, падения напряжения в линейных проводах либо опережают линейные токи по фазе на угол
. Таким образом, падения напряжения в линейных проводах либо опережают линейные токи по фазе на угол 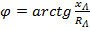 , либо (при
, либо (при 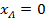 ) совпадают с ними, смещая положения точек a, b и c начал фаз нагрузки от точек (A, B и C) начал фаз генератора на величину падения напряжения между ними, формируя подобно смещению нейтрали – смещение начал фаз.
) совпадают с ними, смещая положения точек a, b и c начал фаз нагрузки от точек (A, B и C) начал фаз генератора на величину падения напряжения между ними, формируя подобно смещению нейтрали – смещение начал фаз.
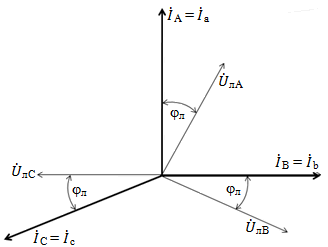
Рис. 19
На рис. 19 приведена векторная диаграмма линейных токов и создаваемых ими падений напряжений в линейных проводах. Модули напряжений в линейных проводах определяются величиной токов в каждом из них, но сдвиги по фазе между напряжением и током формируется только составом сопротивления линии, т.к. 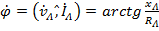 , т.е. во всех фазах цепи одинаковы. При симметричной нагрузке, когда линейные токи одинаковы по величине и смещены по фазе на 120°, падения напряжений в линиях, как и собственно токи, на векторной диаграмме будут представлять из себя равновеликую трехлучевую звезду со сдвигом фаз на 120°.
, т.е. во всех фазах цепи одинаковы. При симметричной нагрузке, когда линейные токи одинаковы по величине и смещены по фазе на 120°, падения напряжений в линиях, как и собственно токи, на векторной диаграмме будут представлять из себя равновеликую трехлучевую звезду со сдвигом фаз на 120°.
Пример векторной диаграммы напряжений трехфазной цепи при симметричной нагрузке / 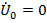 / приведен на рис. 20.
/ приведен на рис. 20.
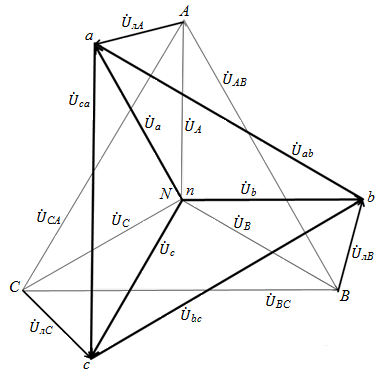
Рис. 20
Здесь тонкими линиями показана векторная диаграмма напряжений на генераторе (равносторонний треугольник линейных напряжений 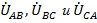 и равновеликая трехлучевая звезда фазных
и равновеликая трехлучевая звезда фазных 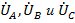 . Жирными линиями показаны смещения начал фаз в линейных проводах
. Жирными линиями показаны смещения начал фаз в линейных проводах 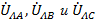 , а также сформированный этим смещением равносторонний треугольник линейных /
, а также сформированный этим смещением равносторонний треугольник линейных / 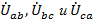 / и равновеликая трехлучевая звезда /
/ и равновеликая трехлучевая звезда / 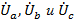 / - фазных напряжений. Как видно из диаграммы, треугольники линейных напряжений и звезды фазных в этом случае поворачиваются друг относительно друга вокруг общего центра. /
/ - фазных напряжений. Как видно из диаграммы, треугольники линейных напряжений и звезды фазных в этом случае поворачиваются друг относительно друга вокруг общего центра. /  0 = 0/
0 = 0/
Понятно, что в случае симметричной нагрузки соотношения между линейными и фазными напряжениями на нагрузке полностью совпадают с соответствующими зависимостями на генераторе, а именно:
- действующие значения фазных напряжений в 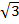 раз меньше действующих значений линейных напряжений (
раз меньше действующих значений линейных напряжений ( 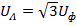 );
);
- фазные напряжения отстают по фазе от соответствующих линейных напряжений на 30°, т.е. 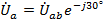 ,
, 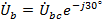 и
и 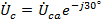 .
.
Понятно, что в этом случае 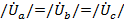 ,
, 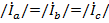 и
и 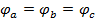 . Это приводит к тому, что мощности в каждой фазе ставятся одинаковыми и, как было показано ранее, общая мощность трёхфазной нагрузки
. Это приводит к тому, что мощности в каждой фазе ставятся одинаковыми и, как было показано ранее, общая мощность трёхфазной нагрузки
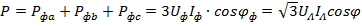 .
.
В случае несимметричной нагрузки наряду со смещением начал фаз будет иметь место еще и смещение нейтральной точки «n» нагрузки относительно нейтральной точки «N» генератора на величину падения напряжения в нулевом проводе (между «n» и «N»).
Симметрия линейных и фазных напряжений на нагрузке будет в этом случае нарушена. Степень искажения напряжений будет определяться как разными по величине и по фазе смещениями 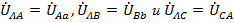 начал фаз генератора и нагрузки, так и смещением
начал фаз генератора и нагрузки, так и смещением 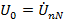 нейтральных точек. Векторная диаграмма для такого случая представлена на рис. 21.
нейтральных точек. Векторная диаграмма для такого случая представлена на рис. 21.
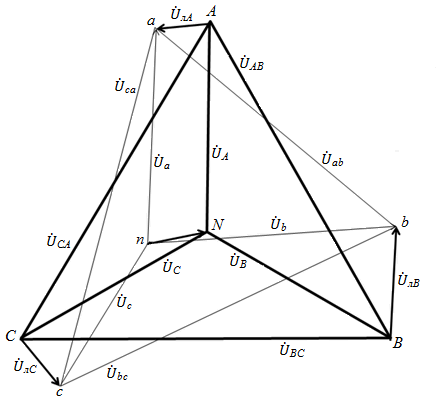
Рис. 21
Построение векторной диаграммы для каждого из рассматриваемых режимов работы является чрезвычайно полезным, поскольку дает наглядное представление о соотношении и взаимном влиянии друг на друга всех электрических величин в цепи.
Отсутствие в трехфазной цепи типа «звезда – звезда» нулевого провода (рис. 22) никаких принципиальных изменений в методы и приемы расчета не вносят. В этом случае мы также имеем цепь с двумя узлами, между которыми включены 3 ветви.
В случае симметричной нагрузки нулевой провод, фактически даже не нужен, ибо 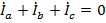 и
и 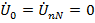 . При несимметричной нагрузке
. При несимметричной нагрузке 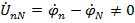 и также легко определяется по методу двух узлов. Отсутствие нулевого провода означает, что
и также легко определяется по методу двух узлов. Отсутствие нулевого провода означает, что 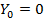 , что приводит к тому, что смещение нейтрали в этом случае возрастает. Соотношение
, что приводит к тому, что смещение нейтрали в этом случае возрастает. Соотношение 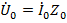 в этом случае теряет смысл и
в этом случае теряет смысл и 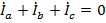 . Это означает, что как линейные, так и фазные токи тесно связаны между собою, замыкание каждого фазного тока «самого на себя» происходит по проводам соседних фаз, так что в каждый момент времени, например,
. Это означает, что как линейные, так и фазные токи тесно связаны между собою, замыкание каждого фазного тока «самого на себя» происходит по проводам соседних фаз, так что в каждый момент времени, например, 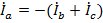 .
.
Все соотношения между напряжениями и токами остаются такими же, как и при наличии нулевого провода. Принципиально такими же остаются и векторные диаграммы при условии, что 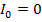 . Линейные токи
. Линейные токи 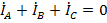 при всех видах нагрузок в этом случае должны образовывать замкнутый треугольник.
при всех видах нагрузок в этом случае должны образовывать замкнутый треугольник.
В подавляющем большинстве практических ситуаций эксплуатации трехфазных электроэнергетических систем доступа к трехфазным генераторам потребители электроэнергии не имеют из-за их удаленности. Никаких проблем для расчета и анализа цепей это не составляет, т.к. в качестве фаз генераторов в этом случае выступают вторичные обмотки трансформаторов распределительных узлов, к которым подключаются потребители, либо просто линейные или фазные напряжения на входе в объект. Такая ситуация имеет место, например, при проектировании и расчете системы электроснабжения многоквартирных домов или предприятий, не имеющих собственных подстанций. В этом случае трехфазная цепь имеет конфигурацию рис. 22.
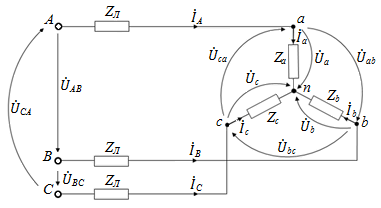
Рис. 22.
Здесь 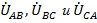 – линейные напряжения на входе к потребителю, которые, как правило, должны представлять из себя симметричную систему напряжений и к которым в полной мере применимы все понятия и определения, введенные для трехфазного генератора. В этом случае сопротивления в линейных проводах A-a, B-b и C-c могут не учитываться
– линейные напряжения на входе к потребителю, которые, как правило, должны представлять из себя симметричную систему напряжений и к которым в полной мере применимы все понятия и определения, введенные для трехфазного генератора. В этом случае сопротивления в линейных проводах A-a, B-b и C-c могут не учитываться 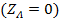 , т.е. точки A-a, B-b и C-c могут быть принудительно совмещены.
, т.е. точки A-a, B-b и C-c могут быть принудительно совмещены.
В случае, если зажимы A, B и C являются клеммами удаленного трансформатора, конечно, следует учитывать сопротивления «жил» подводящего кабеля – линейных проводов.
Расчет цепи в случае рис. 22 и подобных может быть выполнен, например, по методу контурных токов (два ячеечных контура) с учетом того, что 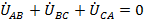 и
и 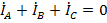 . В то же время можно пойти, например, по пути преобразования треугольника линейных напряжений
. В то же время можно пойти, например, по пути преобразования треугольника линейных напряжений 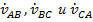 на входе цепи в звезду фазных напряжений
на входе цепи в звезду фазных напряжений 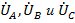 в соответствии с тем, что
в соответствии с тем, что 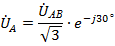 ,
, 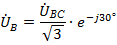 и
и 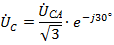 с формированием нулевой точки «N» и свести расчет к рассмотренному ранее методу двух узлов.
с формированием нулевой точки «N» и свести расчет к рассмотренному ранее методу двух узлов.
При этом следует иметь ввиду, что отсутствие нулевого провода при соединении фаз нагрузки по схеме «звезда» оправдано только для случаев симметричной нагрузки.В этом случае при 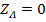 расчет цепи производится просто, с использованием закона Ома, т.к.
расчет цепи производится просто, с использованием закона Ома, т.к. 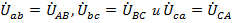 и
и 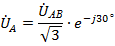 ,
, 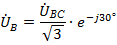 и
и 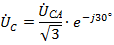 .
.
При этом токи 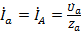 ,
, 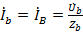 и
и 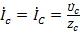 . Это значит, что при симметричной нагрузке достаточно определить токи и напряжения только в одной фазе. В двух других они будут такими же по величине и смещёнными друг относительно друга по фазе на 120°.
. Это значит, что при симметричной нагрузке достаточно определить токи и напряжения только в одной фазе. В двух других они будут такими же по величине и смещёнными друг относительно друга по фазе на 120°.
Подобным образом может быть рассчитана цепь и с несимметричной нагрузкой при наличии в ней нулевого провода, сопротивлением которого (из-за малых расстояний) можно было бы пренебречь. Нейтральная точка «n» в этом случае принудительно помещается в центр треугольника, совмещаясь с «N».
Конечно, токи в фазах в этом случае не будут отвечать условиям симметрии 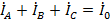 . Можно пойти и по пути преобразования звезды сопротивлений в эквивалентный треугольник по известным правилам
. Можно пойти и по пути преобразования звезды сопротивлений в эквивалентный треугольник по известным правилам
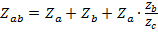 ,
, 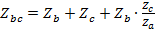 ,
, 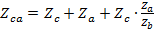 .
.
Однако, этот путь оказывается трудоемким, поскольку требует обратного перехода к звезде.
В практических ситуациях, если эксплуатация трехпроводных трехфазных систем требует использования нейтрального провода. Можно пойти по пути создания искусственной нулевой точки, что в некоторых случаях требуют нужды практической эксплуатации цепей. Схема трехфазного приемника с использованием искусственной нулевой точки «N'» представлена на рис. 23.
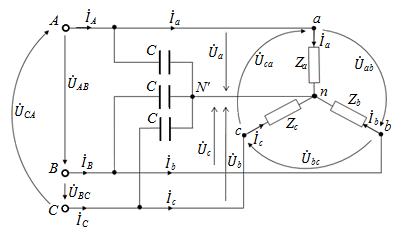
Рис. 23.
С принципиальной точки зрения искусственная нулевая точка может быть создана с помощью любой соединенной по схеме «звезда» системы трех одинаковых сопротивлений. Однако, естественное стремление к уменьшению потерь энергии в таких сопротивлениях требует наличия в них минимальных активных составляющих, либо вовсе отсутствия таковых. В наибольшей степени это условие удовлетворяется емкостями. В связи с симметричностью емкостной нагрузки потенциалы 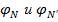 одинаковы.
одинаковы.
Мощности в каждой фазе нагрузки, как было показано ранее, легко вычисляются
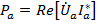 ,
, 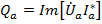 ,
,
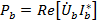 ,
, 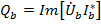 и
и
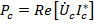 ,
, 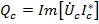 .
.
При этом 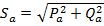 ,
, 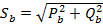 ,
, 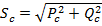 .
.
Мощности трехфазного приемника, в целом, равны
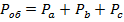 ,
, 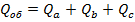 и ясно, что в случае симметричной нагрузки
и ясно, что в случае симметричной нагрузки
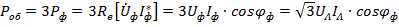 .
.
Аналогично
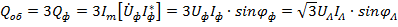 .
.
Соответственно
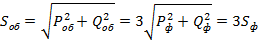 .
.
При этом следует помнить, что активная мощность во всех случаях положительна (электрическая энергия однонаправленно превращается в тепло), т.е. общая мощность есть арифметическая сумма мощностей трех фаз. В то же время реактивные мощности в нагрузках индуктивного и емкостного характера имеют разные знаки, что должно быть учтено при вычислении общей реактивной мощности. Понятно, что при симметричной нагрузке реактивные мощности во всех фазах одинаковы и по величине, и по знакам.
Дата добавления: 2018-05-10; просмотров: 2414;











