Расчет и анализ трехфазных цепей при соединении фаз нагрузки по схеме «треугольник»
Никакого принципиального значения то, по какой схеме (звезда или треугольник) соединены фазы генератора для расчета цепи не имеет. Во всех случаях эксплуатации промышленных систем электроснабжения, как правило, исходят из того, что на стороне генератора имеет место симметричная система ЭДС, поэтому, способ соединения фаз генератора можно выбирать произвольно и при необходимости переходить от одного к другому. Более того, следует понимать, что в подавляющем большинстве случаев эксплуатации трехфазных систем приходится иметь дело не непосредственно с фазами генератора, а с источниками вторичного питания – трехфазными трансформаторами ближайших распределительных пунктов или просто с проводами (жилами кабеля) на входе. Таким образом, все случаи расчета и анализа цепей при соединении фаз нагрузки «треугольником» могут быть сведены к рассмотрению цепи рис. 24.
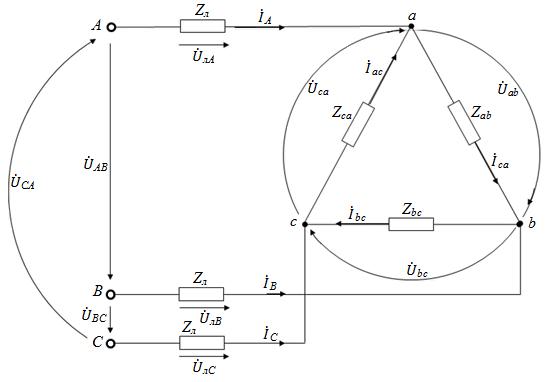
Рис. 24.
Эта цепь представляет из себя обычную сложную цепь переменного тока, содержащую три независимых узла (a, b, c) и три ячеечных контура. Эти контуры четко просматриваются, если избавиться от нахлестов проводов (например, выносом узла «c» за пределы схемы). Оптимальным методом расчета цепи в этом случае может оказаться метод контурных токов (рис. 25).
Система, составляемая по этому методу для рассматриваемого случая, имеет следующий вид:
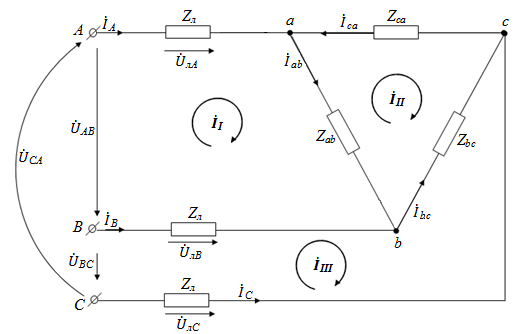
Рис. 25.
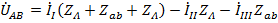 ,
,
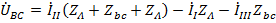 ,
,
 .
.
Понятно, что здесь 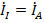 ,
, 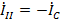 ,
, 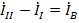 и
и 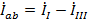 .
.
Конечно, можно преобразовать «треугольник» сопротивлений в эквивалентную «звезду» и, посчитав, что фазы генератора (питающего трансформатора) соединены по схеме «звезда», рассчитать цепь по методу двух узлов. Однако, этот путь в данном случае большой экономии в расчетах не сулит, т.к. требует в конце обратного перехода к схеме «треугольник» с выполнением дополнительных расчетов.
В случае отсутствия сопротивлений в линиях ( 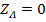 из-за его малости), расчет оказывается чрезвычайно простым, т.к. в этом случае
из-за его малости), расчет оказывается чрезвычайно простым, т.к. в этом случае 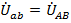 ,
, 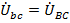 ,
, 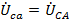 и
и 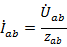 ,
, 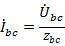 ,
, 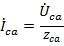 . Токи в линейных проводах при соединении фаз нагрузки по схеме «треугольник» могут быть найдены по первому закону Кирхгофа для узлов «a», «b», и «c»:
. Токи в линейных проводах при соединении фаз нагрузки по схеме «треугольник» могут быть найдены по первому закону Кирхгофа для узлов «a», «b», и «c»:
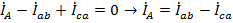 ,
,
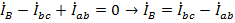 ,
,
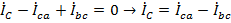 .
.
При этом 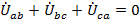 и
и 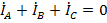 .
.
Эти соотношения для токов и напряжений лежат в основе и расчетов, и построения векторных диаграмм с учетом того, что каждая тройка векторов
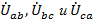
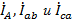
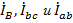
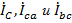
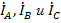
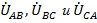
в совокупности друг с другом составляет замкнутые треугольники.
При несимметричной нагрузке и учете сопротивлений линейных проводов потенциалы точек a, b и c на стороне нагрузки будут отличаться от потенциалов точек A, B и C на стороне генератора на величину падения напряжения в соответствующих линейных проводах, т.е.
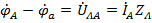 ,
, 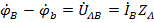 и
и 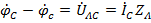 .
.
При том, что 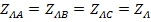 сдвиг по фазе между напряжениями на сопротивлениях линейных проводов и соответствующими токами будет одним и тем же
сдвиг по фазе между напряжениями на сопротивлениях линейных проводов и соответствующими токами будет одним и тем же 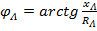 , а величины и собственно начальные фазы этих напряжений определяются величинами и начальными фазами линейных токов. Смещение начал фаз нагрузки от начал фаз генератора в связи с падением напряжений в линейных проводах приводит к искажению напряжений на нагрузке (рис. 26).
, а величины и собственно начальные фазы этих напряжений определяются величинами и начальными фазами линейных токов. Смещение начал фаз нагрузки от начал фаз генератора в связи с падением напряжений в линейных проводах приводит к искажению напряжений на нагрузке (рис. 26).
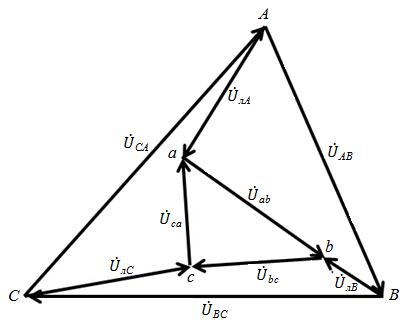
Рис. 26.
При отсутствии сопротивлений в линейных проводах ( 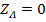 ) смещения начал фаз отсутствуют (
) смещения начал фаз отсутствуют ( 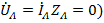 , симметрия напряжений на нагрузке в этом случае восстанавливается, поскольку принудительно обеспечивается равенство
, симметрия напряжений на нагрузке в этом случае восстанавливается, поскольку принудительно обеспечивается равенство 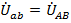 ,
, 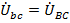 и
и 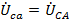 . Однако, при несимметричной нагрузке (
. Однако, при несимметричной нагрузке ( 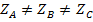 ) токи в фазах и в этом случае будут разными в связи с тем, что
) токи в фазах и в этом случае будут разными в связи с тем, что 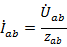 ,
, 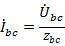 ,
, 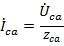 .
.
В случае симметричной нагрузки, когда 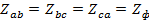 , фазные напряжения
, фазные напряжения 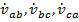 и фазные токи
и фазные токи 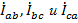 образуют симметричные системы и на векторной диаграмме могут быть представлены либо в виде равновеликих трехлучевых звезд, либо в виде равносторонних треугольников со сдвигами фаз относительно друг друга на 120°.
образуют симметричные системы и на векторной диаграмме могут быть представлены либо в виде равновеликих трехлучевых звезд, либо в виде равносторонних треугольников со сдвигами фаз относительно друг друга на 120°.
Симметрия напряжений при этом обеспечивается и при наличии, и при отсутствии сопротивлений в линейных проводах тем, что падения напряжений в линиях при симметрии линейных токов будут представлять из себя равновеликую трехлучевую звезду со сдвигом векторов на 120°. При этом фазные токи будут отличаться по фазе от своих напряжений на один и тот же угол 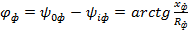 .
.
Для случая, когда фазные нагрузки имеют индуктивный характер, векторная диаграмма имеет вид, подобный рис. 27.
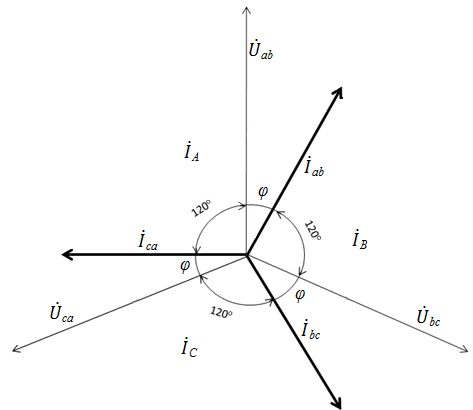
Рис. 27.
Понятно, что линейные токи 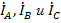 образуют замкнутый равносторонний треугольник с вершинами в началах векторов
образуют замкнутый равносторонний треугольник с вершинами в началах векторов 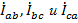 соответствующих фазных токов. Фазные токи при этом имеют вид равновеликой трехлучевой звезды со смещением векторов на 120°.
соответствующих фазных токов. Фазные токи при этом имеют вид равновеликой трехлучевой звезды со смещением векторов на 120°.
Падения напряжений в линейных проводах, формируемые линейными токами будут симметричными. Векторная диаграмма для такого случая представлена на рис. 28 с предположением о том, что сопротивления линий носят индуктивный характер.
Эта векторная диаграмма будет иметь один и тот же вид как при соединении фаз нагрузки по схеме «треугольник», так и по схеме «звезда».
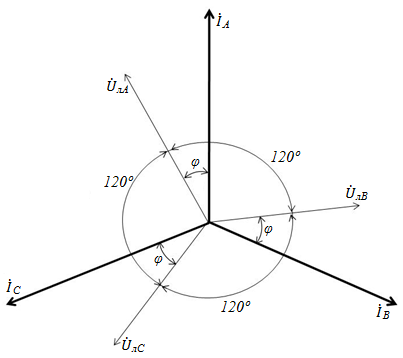
Рис. 28.
Падения напряжения в линиях приводят к смещению друг относительно друга начал фаз генератора и нагрузки A – a, B – b, C – c.
Полная векторная диаграмма напряжений при этом для симметричной нагрузки представлена на рис. 29.
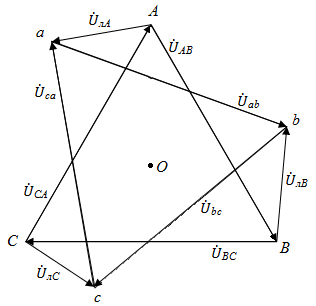
Рис. 29.
В связи с симметрией падений напряжений в линиях, треугольник линейных напряжений на нагрузке, изменяясь по величине, просто поворачивается относительно треугольника линейных напряжений на генераторе вокруг общего центра «0».
Полная векторная диаграмма токов для симметричной нагрузки с учетом полученных ранее зависимостей между линейными и фазными токами представлена на рис. 30.
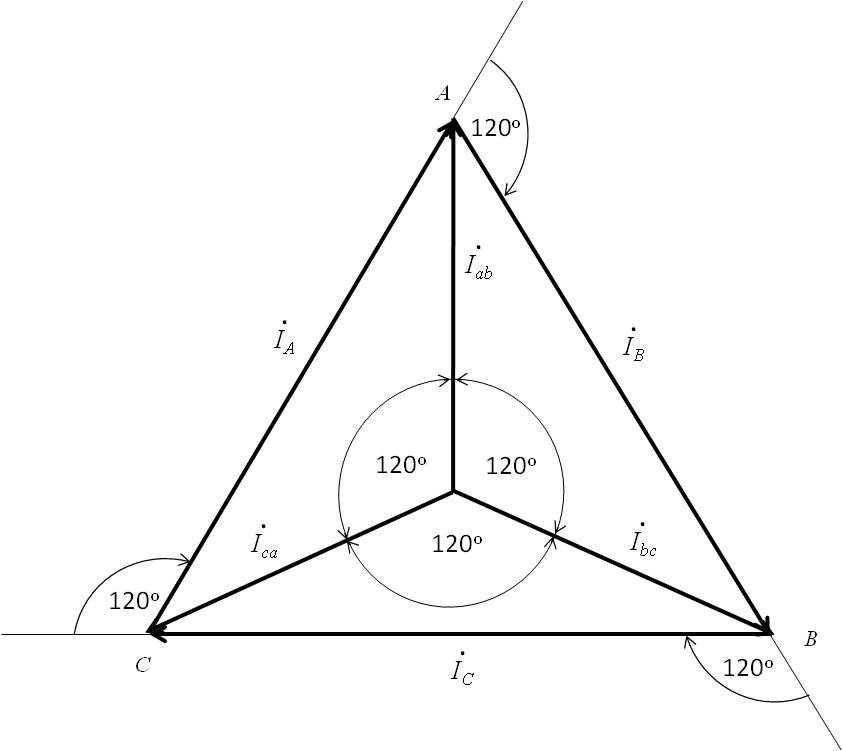
Рис. 30.
Понятно, что при соединении фаз нагрузки по схеме «треугольник» фазные и линейные токи оказываются разными. В общем случае они связаны между собою полученными ранее соотношениями 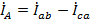 ,
, 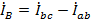 ,
, 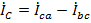 . Но в случае симметричной нагрузки в соответствии с векторной диаграммой рис. 30 эти зависимости упрощаются.
. Но в случае симметричной нагрузки в соответствии с векторной диаграммой рис. 30 эти зависимости упрощаются.
Величина линейного тока в этом случае в 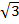 раз больше фазного, а сдвиг по фазе между линейным и соответствующим фазным токами составляет 30°, что приводит к тому, что
раз больше фазного, а сдвиг по фазе между линейным и соответствующим фазным токами составляет 30°, что приводит к тому, что 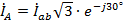 ,
, 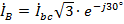 ,
,  . При несимметричной нагрузке эти соотношения не «работают», симметрия токов нарушается.
. При несимметричной нагрузке эти соотношения не «работают», симметрия токов нарушается.
Полная векторная диаграмма токов может быть совмещена с диаграммой напряжений при соблюдении сдвигов по фазам между связанными между собою токами и напряжениями. Такую диаграмму, как правило, строят на комплексной плоскости, принимая начальную фазу одного из векторов (например, одного из фазных напряжений) за ноль и совмещая его с осью вещественных.
Вычисление мощностей в фазах приемника, как и нагрузки, в целом, производится по формулам, аналогичным соответствующим зависимостям при «звезде».
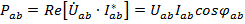 ,
,
 и
и
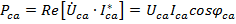
Мощность трехфазной нагрузки, в целом, 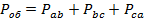 .
.
При симметричной нагрузке 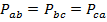 и
и 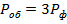 .
.
Аналогично вычисляются реактивные мощности
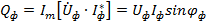 ,
, 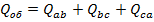 , а при симметричной нагрузке
, а при симметричной нагрузке
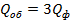 .
.
Полная мощность фазы 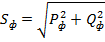 , а нагрузки, в целом,
, а нагрузки, в целом, 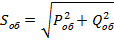 .
.
Простое суммирование полных фазных мощностей 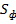 для вычисления общей
для вычисления общей 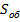 допустимо только при симметричной нагрузке, когда
допустимо только при симметричной нагрузке, когда 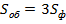 .
.
Дата добавления: 2018-05-10; просмотров: 4161;











