Численные методы решения уравнения движения поезда

Для решения уравнения движения поезда с помощью ЭВМ используют численные методы интегрирования. Принципиально они аналогичны аналитическому и графическому методам. Различия состоят лишь в математической формализации зависимостей 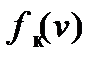, 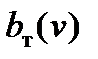и решении уравнения движения поезда.

Сущность численных методов заключается в замене нелинейного дифференциального уравнения движения поезда линейным дифференциальным, решение которого с достаточной для практики точностью приближается к решению нелинейного уравнения, то есть в линеаризации уравнения движения путём замены его линейным уравнением с постоянными коэффициентами. Основным допущением, как и в ранее рассмотренных методах, применяется принцип малых отклонений входящих в уравнение координат от тех значений, которые приняты в качестве исходных для линеаризации.

Известно много различных методов численного интегрирования дифференциальных уравнений: Л.Эйлера, Чаплыгина, Рунге – Кутта, Адамса и др. Академик А.Н. Крылов разделил приёмы нахождения приближённых решений дифференциальных уравнений на группы:

2. Разложение общего интеграла в ряды.

3. Применение способа последовательных приближений.

4. Приближённое численное интегрирование.

При выполнении тяговых расчётов, одним из методов численного интегрирования, достаточно найти частное решение, удовлетворяющее начальным условиям, в виде таблицы или графика кривой, представляющих решение уравнения движения поезда.