Основные принципы определения скорости движения поезда
Определение скорости движения поезда определённой массы по участку пути можно выполнить аналитическим, графоаналитическим или численными методами.
Характеристику скорости движения поезда, изображённой на графике в функции от пути, называют кривой скорости движения.
Аналитический метод расчёта скорости движения поезда основан на определении равновесных скоростей на уклонах элементов продольного профиля. По сути, это задача, обратная определению веса состава. Для её решения необходимы исходные данные:
· тип локомотива, его масса, тяговая характеристика;
· характеристика и масса состава;
· подробные сведения об участке эксплуатации: план и профиль пути.
Скорость движения заданного поезда на заданном участке, крутизной 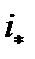 , определяется решением уравнения при равномерном движении, когда
, определяется решением уравнения при равномерном движении, когда
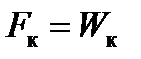 , (1)
, (1)
где 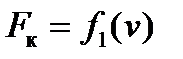 ‑ исходная зависимость.
‑ исходная зависимость.
Правая часть уравнения
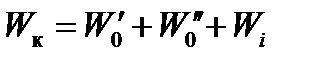 ,
,
включает: полное основное сопротивление локомотива
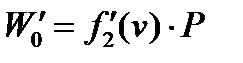 , Н;
, Н;
полное основное сопротивление состава
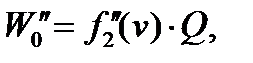 Н;
Н;
дополнительные сопротивления от профиля пути
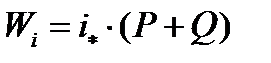 , Н.
, Н.
В результате получается развёрнутая форма уравнения движения поезда на уклоне 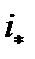 :
:
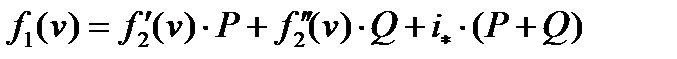 . (2)
. (2)
Полученное уравнение следует решать относительно переменной 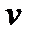 и тогда на
и тогда на 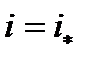 можно определить равновесную скорость
можно определить равновесную скорость 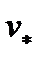 . Затем, подставляя в уравнение значения следующих уклонов, будут получены равновесные скорости для этих уклонов.
. Затем, подставляя в уравнение значения следующих уклонов, будут получены равновесные скорости для этих уклонов.
Скорости установившегося равномерного движения на уклонах элементов продольного профиля называются равновесными.
По результатам расчётов для нескольких уклонов строится график зависимости 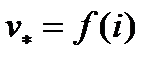 , по которому находят величины равновесных скоростей для уклонов всех элементов участка пути.
, по которому находят величины равновесных скоростей для уклонов всех элементов участка пути.
Данная задача решается с помощью вычислительной техники.
Равновесные скорости для различных уклонов продольного профиля могут быть получены путём графоаналитического построения.
В начале решается уравнение 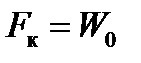 , которое соответствует движению поезда на прямом горизонтальном пути. Здесь
, которое соответствует движению поезда на прямом горизонтальном пути. Здесь
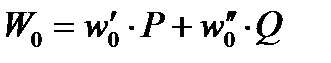 ,Н. (3)
,Н. (3)
В системе координат «сила – скорость» строится график тяговой характеристики заданного локомотива 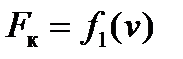 . В той же системе координат строится график
. В той же системе координат строится график 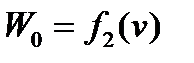 полного основного сопротивления движению поезда на прямом горизонтальном пути. Точка пересечения графиков силы тяги и основного сопротивления даёт равновесную скорость
полного основного сопротивления движению поезда на прямом горизонтальном пути. Точка пересечения графиков силы тяги и основного сопротивления даёт равновесную скорость 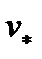 движения принятой массы поезда на прямом горизонтальном пути.
движения принятой массы поезда на прямом горизонтальном пути.
Затем производится расчёт 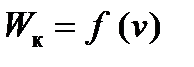 при движении поезда на затяжных подъёмах
при движении поезда на затяжных подъёмах 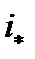 , на которых устанавливается равновесная скорость, при которой
, на которых устанавливается равновесная скорость, при которой 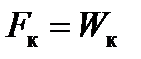 . Полученные значения
. Полученные значения 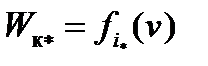 служат для построения графиков в той же системе координат. Точки пересечений графиков дают значения равновесных скоростей для заданного поезда.
служат для построения графиков в той же системе координат. Точки пересечений графиков дают значения равновесных скоростей для заданного поезда.
Пример 1.Поезд массой 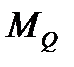 = 3000 т везёт тепловоз ТГ102,
= 3000 т везёт тепловоз ТГ102, 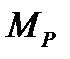 = 164 т. Состав состоит из четырёхосных гружёных вагонов массой
= 164 т. Состав состоит из четырёхосных гружёных вагонов массой 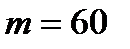 т. Определить равновесные скорости для заданного профиля участка пути (таблица 1) и определить время хода от ст. А до ст. В.
т. Определить равновесные скорости для заданного профиля участка пути (таблица 1) и определить время хода от ст. А до ст. В.
Профиль пути
Таблица 1
| № элемента | |||||||
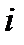 , ‰ , ‰
| -3 | ||||||
| S, м |
Решение. 1. Из ПТР определяем значения тяговой характеристики (кгс) тепловоза ТГ102 и переводим их в систему СИ. По полученным значениям силы тяги в Н, строим график (рисунок 1) в функции скорости движения.
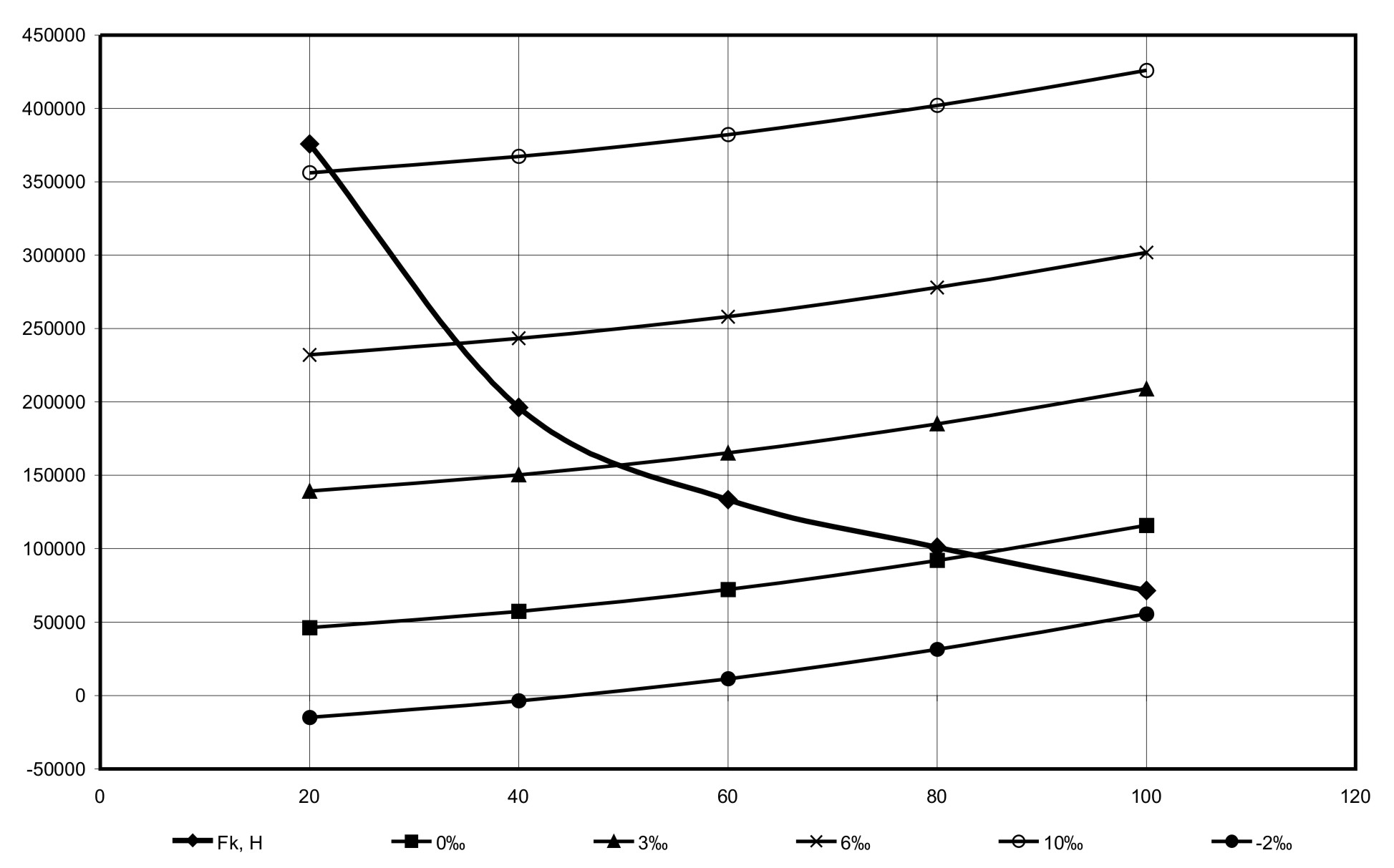
Рисунок 1. Графическое определение равновесных скоростей для уклонов и профиля пути.
2. Рассчитываем и сводим в таблицу (2а и 2б) значения: 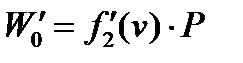 ;
; 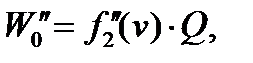 ;
; 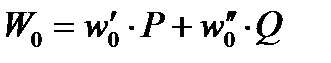 ,
,
где 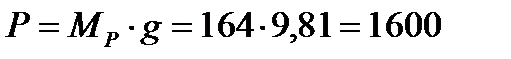 кН;
кН; 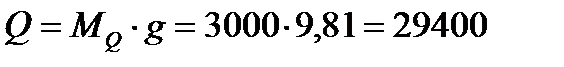 кН.
кН.
3. Задаваясь разными значениями 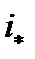 , определяем значения,
, определяем значения, 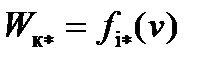 и результаты расчёта также сводим в таблицы (2 а, б)
и результаты расчёта также сводим в таблицы (2 а, б) 
4. В тех же координатах на графике рисунок 1 (силы тяги) строим зависимости 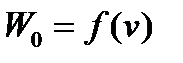 и
и 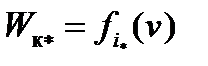 , по которым находим равновесные скорости
, по которым находим равновесные скорости 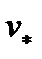 при различных значениях
при различных значениях 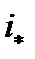 .
.
Равновесные скорости движения поезда в зависимости от величины уклона сводим в таблицу 3.
По полученным значениям равновесных скоростей в зависимости от уклонов строим график (рисунок 2), где по ординате откладываем значения уклонов (подъёмов), по оси абсцисс – скорость движения поезда. Этот график позволяет легко установить равновесные скорости на заданном участке пути (рисунок 3).
Определение равновесных скоростей в зависимости от уклонов и режима движения
Таблица 2 а
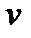 км/ч
км/ч
| 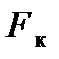 Н
Н
| 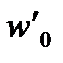 Н/кН
Н/кН
| 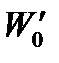 Н
Н
| 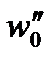 Н/кН
Н/кН
| 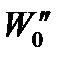 Н
Н
| 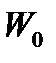 Н
Н
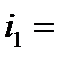 0 0
| 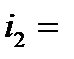 3‰ 3‰
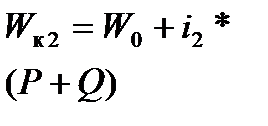
| 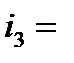 6‰ 6‰
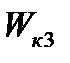
| 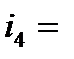 10‰ 10‰
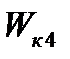
|
| 2,22 | 1,45 | ||||||||
| 2,78 | 1,8 | ||||||||
| 3,58 | 2,26 | ||||||||
| 4,62 | 2,88 | ||||||||
| 5,9 | 3,62 |
Таблица 2 б
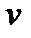 км/ч
км/ч
| 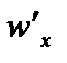 Н/кН
Н/кН
| 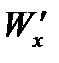 Н
Н
| 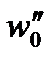 Н/кН
Н/кН
| 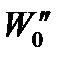 Н
Н
| 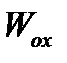 Н
Н
| 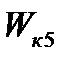
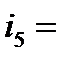 -2‰ -2‰
|
| 2,76 | 1,45 | -14970 | ||||
| 3,4 | 1,8 | -3640 | ||||
| 4,32 | 2,26 | +11356 | ||||
| 5,52 | 2,88 | +31504 | ||||
| 7,0 | 3,62 | +55628 |
Результаты расчётов в таблице 2а и 2б для движения поезда в режимах тяги и выбега для разных уклонов пути нанесены на график (рисунок 1). Точки пересечений тяговой характеристики 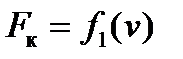 с характеристиками полных сопротивлений движению поезда
с характеристиками полных сопротивлений движению поезда 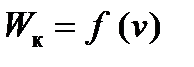 на разных уклонах и есть искомые равновесные скорости.
на разных уклонах и есть искомые равновесные скорости.
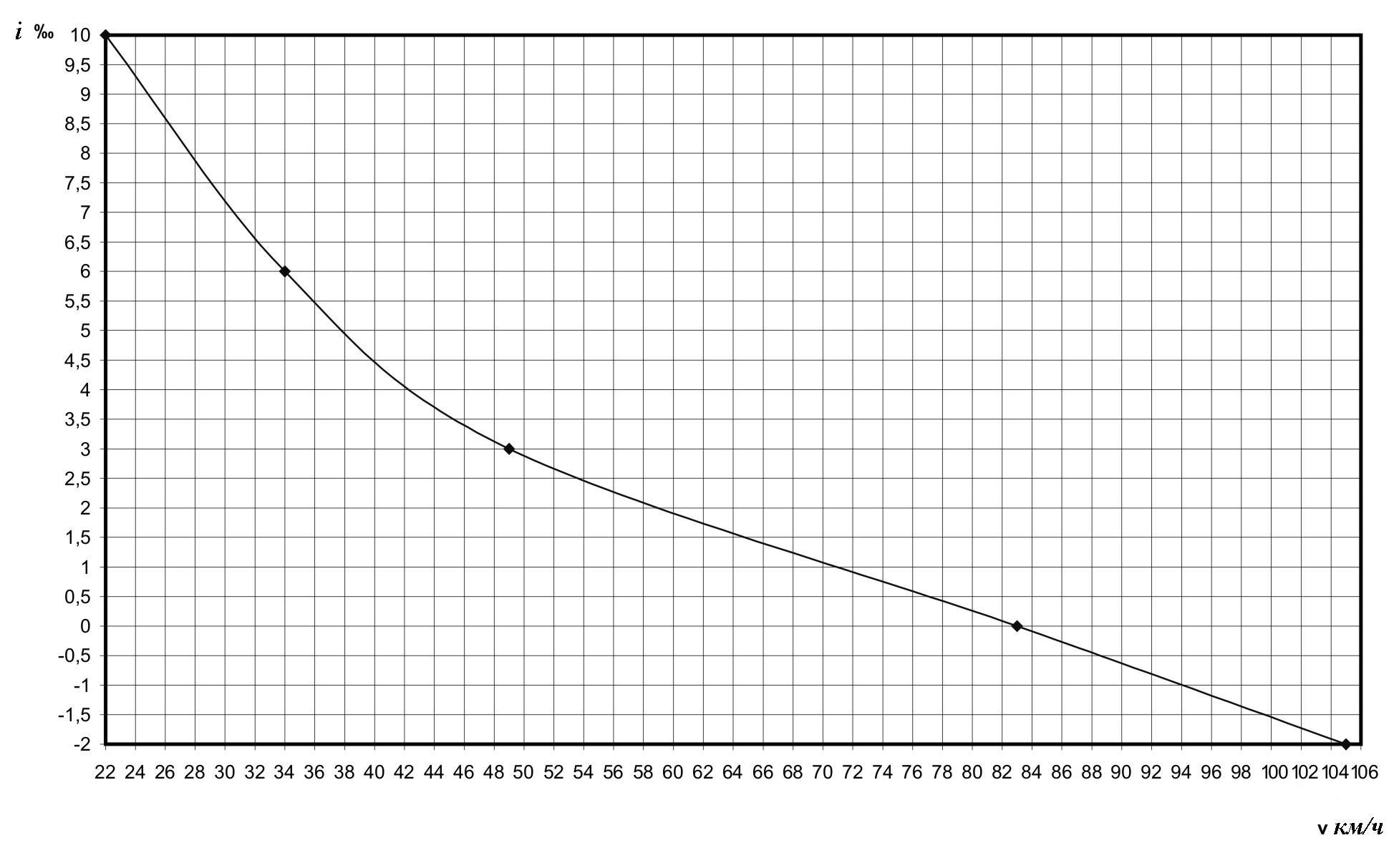
Рисунок 2. Вспомогательная характеристика равновесных скоростей.
Координаты установленных равновесных скоростей сведены в таблицу 3 и по ним построена вспомогательная характеристика (рисунок 2) для построения графика равновесных скоростей на заданном участке эксплуатации (рисунок 3).
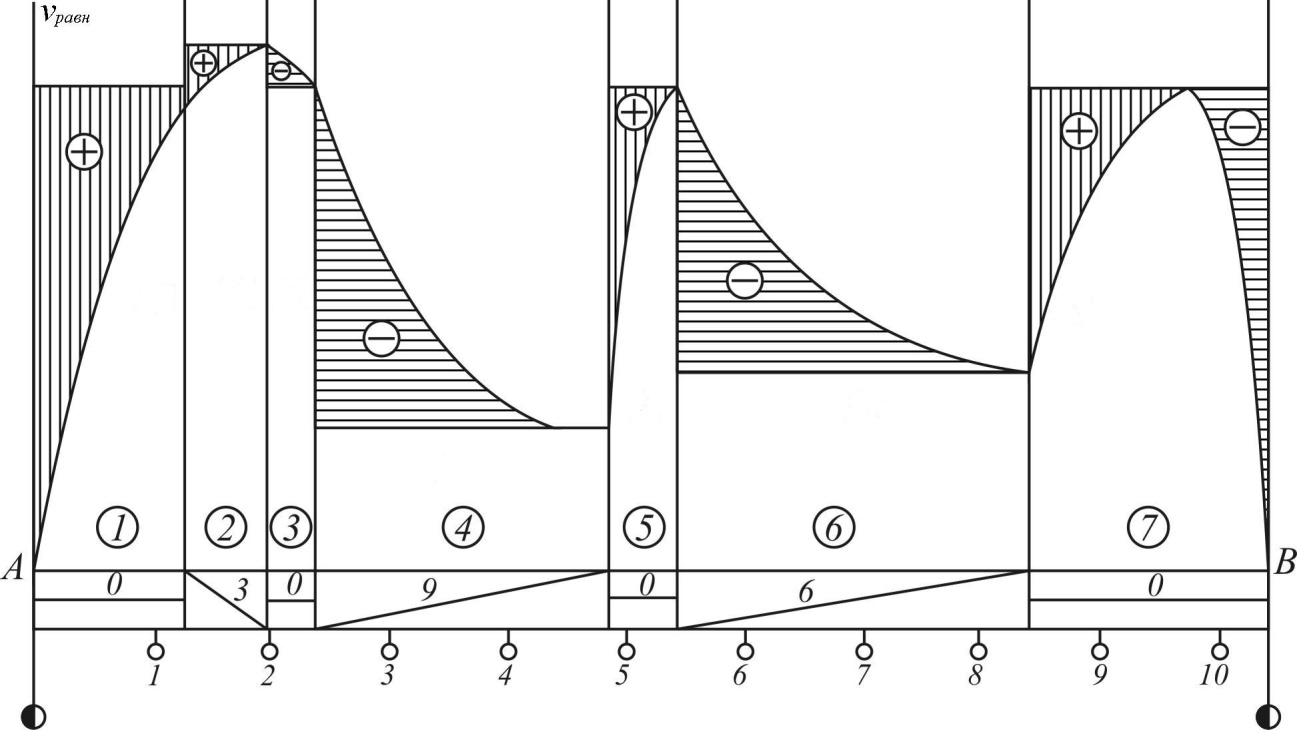
Рисунок 8.3. График равновесных (установившихся) скоростей движения поезда при движении по различным элементам профиля пути.
Координаты равновесных скоростей
Таблица 3
| Уклоны i*, ‰ | - 2 | ||||
Равновесные скорости 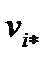 км/ч км/ч
|
На (рисунке 3) построен график 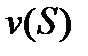 . По оси абсцисс отложен профиль заданного участка пути, горизонтальные линии соответствуют равновесным скоростям на каждом элементе, определённых по вспомогательному графику (рисунок 2). На первом элементе i = 0 и скорость v*= 83 км/ч. На втором элементе – спуск, крутизной i = -3 ‰, поезд переходит в режим выбега и может достичь равновесной скорости более v*=100 км/ч. По табл. 8.4 устанавливаем равновесную скорость на спуске, крутизной i = -3 ‰, v*=90 км/ч.
. По оси абсцисс отложен профиль заданного участка пути, горизонтальные линии соответствуют равновесным скоростям на каждом элементе, определённых по вспомогательному графику (рисунок 2). На первом элементе i = 0 и скорость v*= 83 км/ч. На втором элементе – спуск, крутизной i = -3 ‰, поезд переходит в режим выбега и может достичь равновесной скорости более v*=100 км/ч. По табл. 8.4 устанавливаем равновесную скорость на спуске, крутизной i = -3 ‰, v*=90 км/ч.
Допустимую скорость на спуске для поездов, имеющих расчётный тормозной коэффициент не менее 0,33, рекомендуется устанавливать в зависимости от крутизны спуска таблице 4.
Таблица 4 Допустимая скорость на спуске
| i, ‰ | до – 10 | - 11 … -15 | - 16 … -20 | - 21 … -24 | -25 … - 30 |
| n, км/ч |
Время движения поезда по каждому элементу профиля пути при равновесной (установившейся) скорости, мин, определяется по формуле
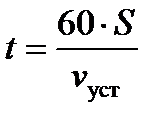 , мин. (4)
, мин. (4)
Чтобы определить время хода по перегону или участку, значения t на каждом элементе пути суммируют. Результаты таких расчётов сводят в таблицу 5.
Таблица 5 Время хода по перегону
| Перегон | № Эле-мента | Длина элемента, км | Уклон ‰ | Равновесная скорость, км/ч | Время прохождения элемента, мин | Поправка на разгон и замедление, мин | Время хода по перегону, мин |
| А | 1,3 | 0,94 | 2,0 | 2,94 | |||
| - | 0,7 | - 3,0 | 0,46 | - | 3,4 | ||
| - | 0,4 | 0,29 | - | 3,69 | |||
| - | 2,5 | 9,0 | 6,0 | - | 9,69 | ||
| - | 0,6 | 0,43 | - | 10,12 | |||
| - | 3,0 | 6,0 | 5,29 | - | 15,41 | ||
| В | 2,0 | 1,44 | 1,0 | 17,85 |
В действительности, поезд достигает равновесной скорости очень редко. На первом элементе идёт разгон и скорость поезда, как правила, не достигает установившегося значения, а на подъёмах скорость может меняться значительно.
Время tр, необходимое на разгон поезда после остановки и tт, затрачиваемое на торможение до остановки на раздельном пункте, учитывают, вводя соответствующие поправки. Поправка на разгон поезда tр в среднем принимается 2 мин, а на замедление поезда – 1 мин. Для электропоездов поправку на разгон принимают 0,5 мин, а на замедление – 0,4 мин.
Следовательно, время хода по перегону составит
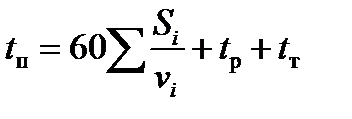 , мин. (5)
, мин. (5)
Метод равновесных скоростей используют для оценки времени хода при предварительных прикидочных расчётах на участках, подлежащих модернизации или электрификации.
Дата добавления: 2017-11-21; просмотров: 3834;











