Лекция №13. Построение кривой скорости с учетом длины и массы поезда.

В ближайшей перспективе развития железнодорожного транспорта масса поезда достигнет 15 – 20 тыс. т, а его длина – 2 – 3 км и более. В этих условиях моделирование движения поезда традиционными методами теории тяги поездов нуждается в уточнении.

Существующие приближённые методы решения дифференциального уравнения движения поезда с учётом его массы и длины, разработанные Н.Е. Жуковским, С.А. Чаплыгиным, А.Н. Крыловым, не нашли практического применения из-за их сложности и недостаточной точности. При нахождении поезда одновременно на 5 – 10 и более элементах профиля решение уравнения движения поезда этими методами практически невозможно даже с использованием ЭВМ, а современные поезда длиной 1,5 – 2,0 км располагаются одновременно на 15 – 20 элементах попикетного (длина элемента 100 м) профиля. Использование спрямлённого обычным методом профиля не обеспечивает требуемой точности решений.

Более простым и достаточно точным является метод построения расчётного тягового профиля с учётом длины и массы поезда. При этом решение уравнения движения поезда ведётся традиционными способами (аналитическими и графическими), а изменяется только метод подготовки для расчётов исходного профиля пути.

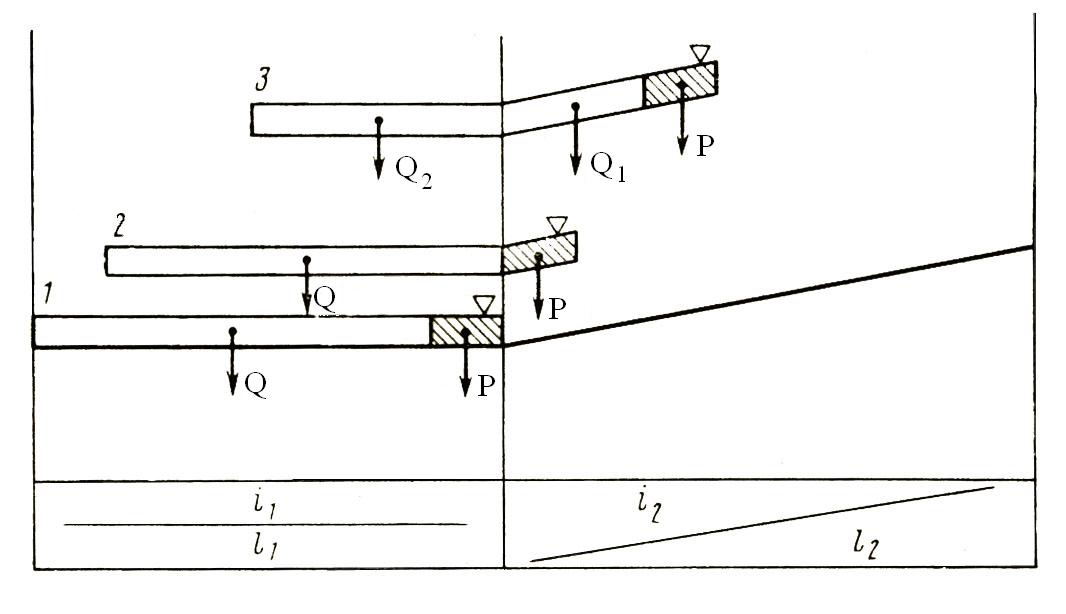
Рисунок 1. Расположение поезда на профиле пути.

Перед входом поезда на уклон 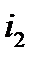(рисунок 1) его полное сопротивление движению (положение 1)

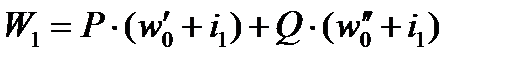, Н. (1)

В положении 2 полное сопротивление движению поезда

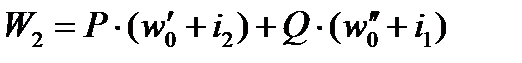, Н, (2)

что равнозначно вступлению поезда на эквивалентный уклон 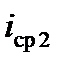, определяемый из выражения

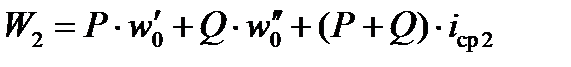, Н. (3)

Из сопоставления выражений (1) и (2) определяется

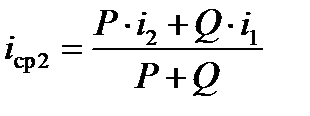, ‰ или (Н/кН). (4)

В положении 3 полное сопротивление поезда

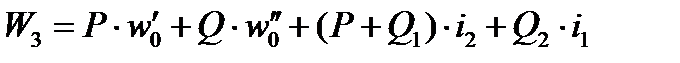, Н (5)

или

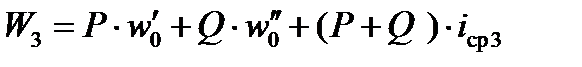, Н. (6)

Из сопоставления выражений (5) и (6) получим:

,

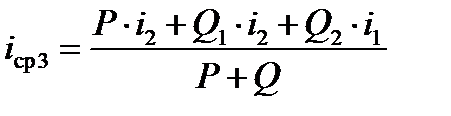где 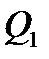- часть веса состава располагается на втором элементе профиля пути, а 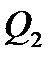- другая часть веса состава ещё находится на первом элементе профиля пути.

При расположении поезда на трёх элементах профиля пути

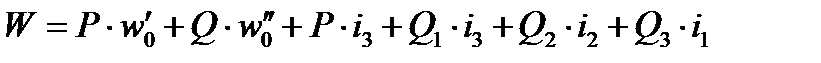
или

,

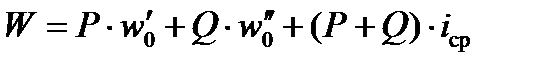откуда среднее значение уклона, действующего на поезд в этом положении

.

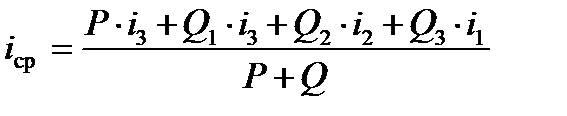Этот способ построения расчётного (с учётом длины и веса поезда) профиля пути, основные положения которого предложены Ю.В. Ломоносовым, целесообразно применять в том случае, когда задан подробный попикетный профиль и план пути. Применение попикетного профиля хотя и увеличивает объём расчётов, но компенсируется существенным повышением точности для определения скорости движения поезда. В этом случае выражение определения среднего уклона, действующего на поезд (рисунок 2), принимает вид

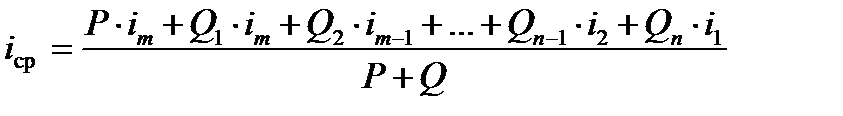. (7)

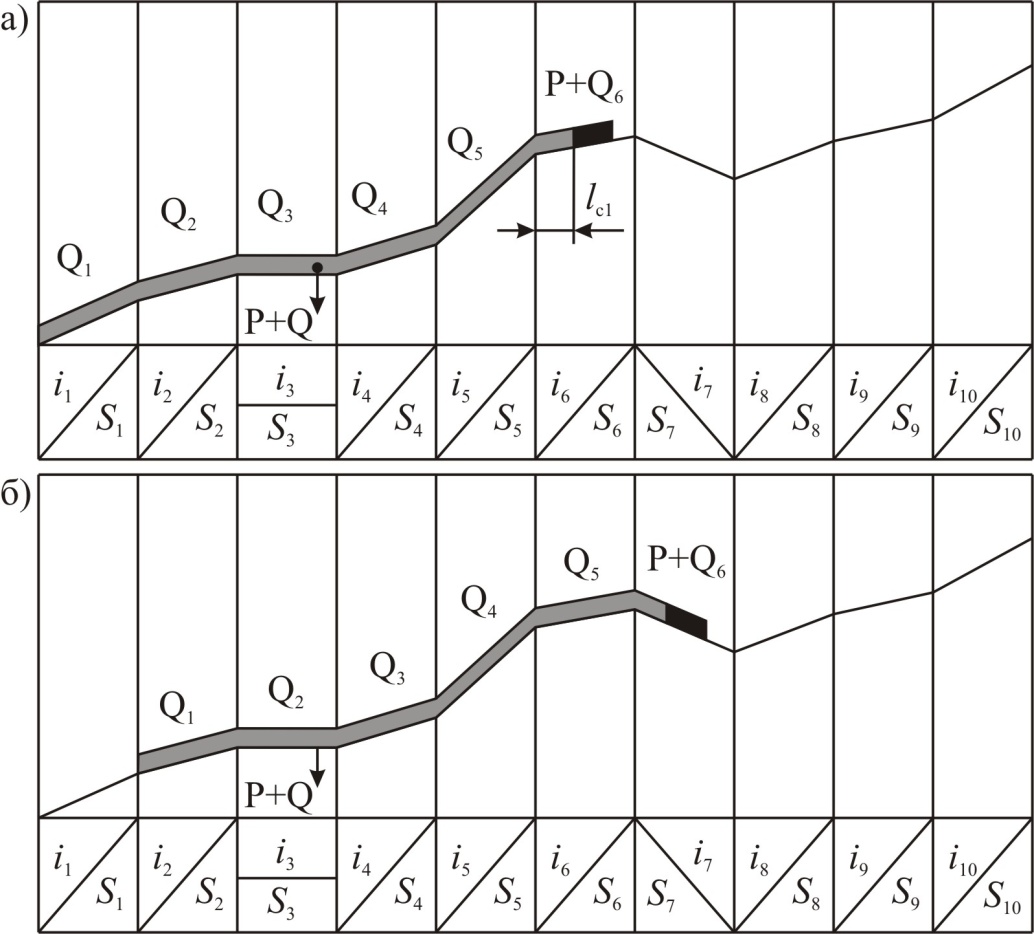
Рисунок 2. Расположение поезда на нескольких элементах попикетного профиля.

Расчёты выполняются в следующей последовательности.

Вначале определяется среднестатистическая длина и вес поезда (в кН). Если на участке имеются кривые, то они заменяются приведёнными уклонами на каждом элементе попикетного профиля, на котором они расположены, по выражению

.

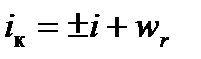Если предположить, что вес 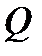состава равномерно распределён по его длине 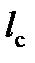, то выражение (7) для первого положения поезда, изображённого на рисунке 2, примет вид

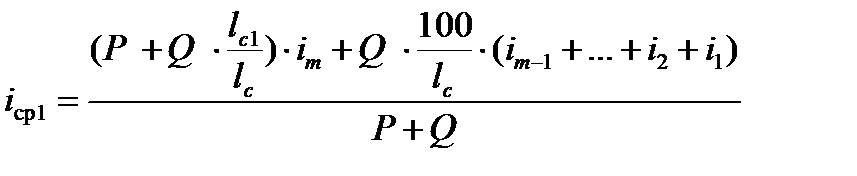, (8)

так как при попикетном профиле 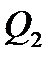= = 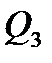… = = 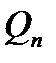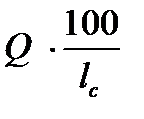, а ,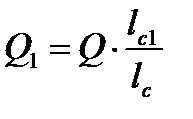

то выражение (7) может быть представлено в виде

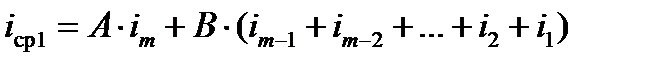, (9)

где

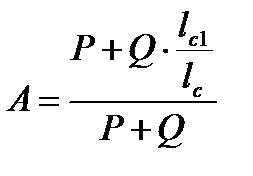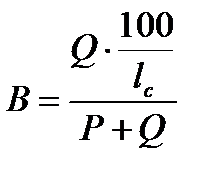; , (10)

где 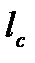- общая длина состава, м;

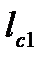- длина части состава, располагающаяся на одном с локомотивом элементе профиля, м.

Для удобства расчётов конечную точку поезда «привязывают» к границе элемента профиля.

Перемещая поезд вперёд на 100 м, получают выражение для положения поезда 2

.

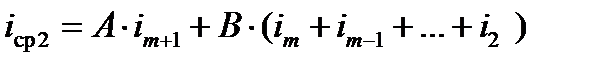Для положения 3

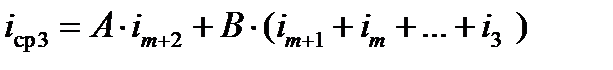
и так далее.

Полученные значения средних уклонов 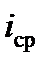- показывают значения уклонов, в каждый момент времени соответствующих положениям поезда: 1, 2, 3 и т. д. Для расчётов же необходимо иметь непрерывный профиль. Для этого определяют расчётные значения уклонов как средние алгебраические между двумя соседними 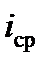, то есть

;

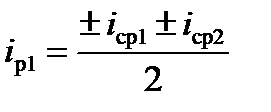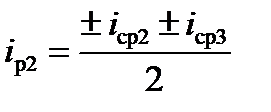
и так далее. Значения уклонов во все формулы следует подставлять со своими знаками. Значения уклонов в каждый момент времени могут быть приведены не только для центра тяжести поезда, но и для любой точки. Так, например, если «привязать» мгновенные и расчётные значения уклонов для головы поезда, то можно затем производить непосредственное сравнение расчётных значений скорости с показаниями скоростемера на локомотиве или с данными скоростемерной ленты.

Для сокращения объёма расчётов, когда приходится выполнять построение кривых скорости для одного и того же участка пути неоднократно, необходимо один раз построить кривую скорости по расчётному тяговому профилю, а затем объединить несколько элементов расчётного профиля в участки, на которых кривая скорости может быть заменена прямыми отрезками. Практика показывает, что при этом количество элементов профиля на перегоне сопоставимо с количеством элементов при спрямлении обычным способом, точность построения кривой скорости по такому спрямлённому профилю возрастает в сравнении с кривой скорости, рассчитанной обычным способом.

Пример.Длина грузового поезда 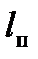=660 м, длина локомотива 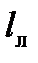= 25 м; длина состава 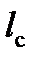=635 м; масса состава 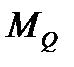= 2000 т; масса локомотива 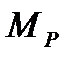= 160 т. Длина части состава, которая располагается на одном с локомотивом элементе, 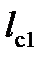= 35 м. Определить тяговый профиль на заданном участке попикетного профиля и плана пути. (Рисунок 3).

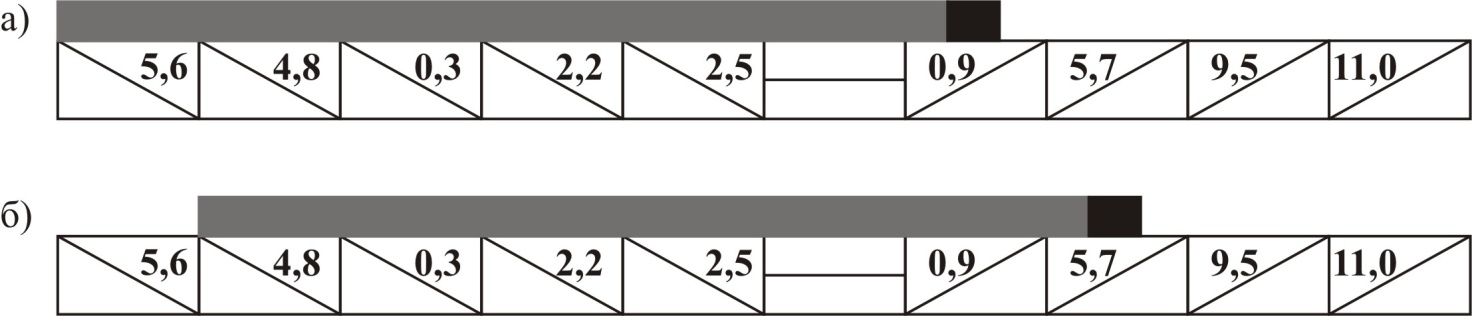
Рисунок 3. Пример расположения поезда на профиле пути.

Решение. По выражению (8.14) определяются средние значения уклонов, действующих на поезд в положениях 1, 2, 3, 4, и т. д. (рис. 8.11). Эти значения уклонов приведены к центру тяжести поезда (цт).

Вначале определяется вес состава и вес локомотива:

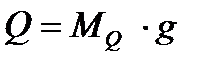= 2000 · 9,81= 19620 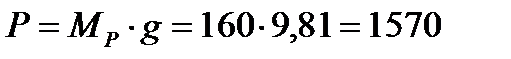кН;

кН.

Предварительно рассчитываются значения коэффициентов 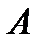и 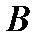в выражении (8.15):

;

.

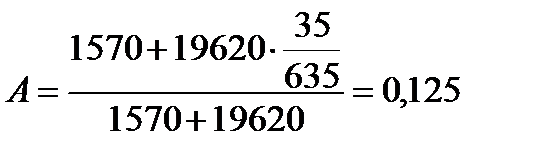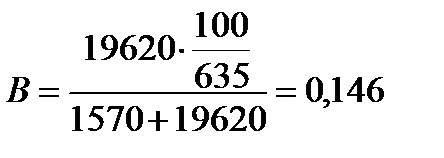При первом положении поезда

‰.

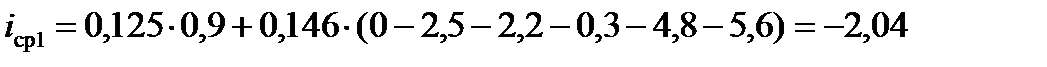При втором положении поезда

‰.

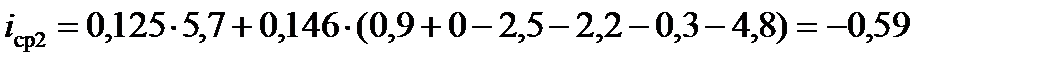При третьем положении поезда

‰.

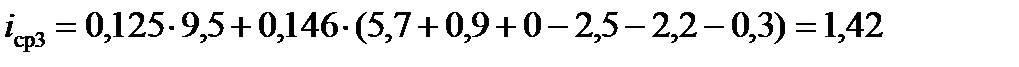При четвёртом положении поезда

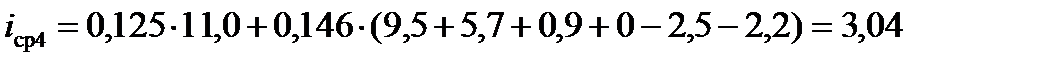‰ и т. д.

Затем рассчитывают значения уклонов тягового профиля:

‰;

‰;

‰

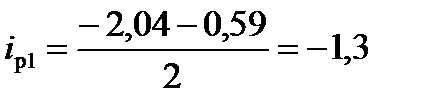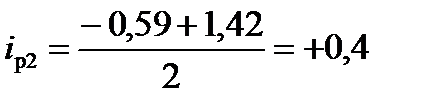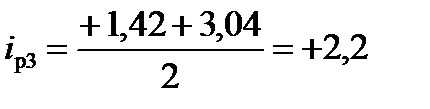и т. д.