Приведение величин вторичной обмотки к числу витков первичной обмотки

При решении задач удобно реальный трансформатор, имеющий различные числа витков обмоток w₁ и w₂, заменить эквивалентным трансформатором, у которого обе обмотки будут одинаковые числа витков (w₂=w₁).

Эквивалентный трансформатор, у которого w₂=w₁, называется приведенным.

Указанная замена будет правомерной, если все энергетические и электромагнитные соотношения в реальном и приведенном трансформаторах будут одинаковы и следовательно, не отразятся на режиме работы первичной обмотки. Исходя из этого определяются токи, ЭДС, напряжения и сопротивления вторичной цепи приведенного трансформатора. Эти величины называются приведенными к числу витков первичной обмотки или просто приведёнными и обозначаются штрихом.

Определим эти величины. Так как w'₂=w₁, то

Е'₂ = Е₁= Е₂ w₁/ w₂= Е₂n_т .

Аналогично U'₂ = U₂n_т.

МДС вторичной обмотки приведенного трансформатора должна быть равна МДС вторичной обмотки реального трансформатора, т.е.

I'₂w₁= I₂w₂,

откуда

I'₂= I₂ (w₂/w₁)= I₂(1/n_т), (3.10)

при этом полная мощность вторичной обмотки остаётся неизменной:

U'₂ I'₂= U₂n_т I₂(1/n_т) = U₂ I₂

Потери мощности во вторичной обмотке этих трансформаторов должны быть одинаковыми:

(I'₂)² r'₂ = (I₂)² r₂.

С учётом (3.10) получим

r'₂= r₂ (w₁/ w₂)² = r₂ (n_т)² .

Аналогично получим

x'₂= x₂ (w₁/ w₂)² = x₂ (n_т)² .

Откуда следует, что полное сопротивление вторичной обмотки приведённого трансформатора Z'₂ = Z₂(n_т)².

Если сопротивление цепи нагрузки Z_нг , то Z'_нг = Z_нг(n_т)².

Уравнения приведённого трансформатора:

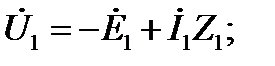(3.11)

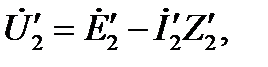(3.12)

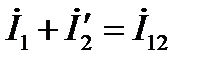. (3.13)