Устойчивость численного решения

Выше было показано, что численное решение системы дифференциальных уравнений (1) с матрицей L собственных значений эквивалентно точному решению системы уравнений со смещенной матрицей собственных значений L+dL, определяемой выражением (19). Так как входящие в него матрицы диагональны, то легко написать соответствующие скалярные соотношения:

eZkh = e(Zk+dZk)h= ebkh , bk= Zk+dZk , k=1…n (2.1.23)

где bk– смещенные собственные значения.

Устойчивость исходной системы уравнений (1) или, что то же самое, ее точного решения, определяется следующими условиями:

Re(Zk) < 0 , k = 1…n.

При численном решении дифференциального уравнения корни смещаются на dZk. Это может привести к тому, что какой-то смещенный корень bk переместится в правую полуплоскость, что будет соответствовать неустойчивости численного решения.

Условием устойчивости численного решения является, очевидно, соотношение:

Re(bkh) = Re[(Zk+dZk)h] < 0 , k=1…n. (2.1.24)

Из (23) с учетом (18) найдем значение смещенного корня:

bkh = ln(eZkh) = ln[1+Zkh+…+(Zkh)r/r!] (2.1.25)

Представим eZkhв виде комплексного числа:

eZkh= u + iv = Neiф, (2.1.26)

N = 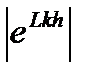= 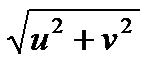, ф= arctg(v/u)

Учитывая (25) и (26) , условия устойчивости численного решения (24) можно записать:

Re(bk) = ln 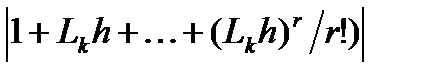< 0 (2.1.27)

В координатах u и v из (26) областью устойчивости является круг единичного радиуса с центром в начале координат:

u2+ v2< 1 (2.1.28)

Соотношения (27) и (28) позволяют избежать грубых ошибок при выборе шага дискретизации h и порядка

метода r.