Трёхфазные трёхпроводные и четырехпроводные электрические цепи

1 23

Трёхфазная четырёхпроводная система питания потребителей электроэнергии, широко распространённая в низковольтных сетях, позволяет получить для питания потребителей два напряжения − линейное U_л

и фазное U_ф.

При смешанной силовой и осветительной нагрузках силовые низковольтные потребители электроэнергии питаются линейными напряжениями (U_л=660; 380; 220 В). Для осветительной нагрузки используются фазные напряжения U_ф=220; 127 В.

В трёхфазных четырёхпроводных электрических цепях при наличии

линейных проводов, соединяющих начала фаз источника питания и

потребителя электроэнергии, имеется также нейтральный провод, соединяющий нейтральную точку Nисточника с нейтральной точкой ппотребителя (рис. 3.1), что обеспечивает симметрию фазных напряжений источника и потребителя, так как нейтральный провод уравнивает потенциалы нейтральных точек Nи п.

В четырёхпроводных электрических цепях фазы источника и фазы потребителя соединяются всегда «звездой».

При несимметричной нагрузке комплексные сопротивления фаз потребителя не одинаковы (Z_a≠Z_b≠Z_c), при этом комплексное напряжение 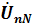, действующее между нейтральными точкамиNи псистемы, определяют по методу двух узлов

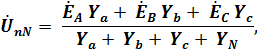
где 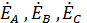,E_C − комплексные ЭДС источника питания;

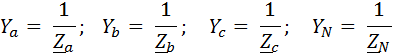
− комплексные

проводимости фаз потребителя и нейтрального провода.

При симметричной нагрузке Z_a= Z_b = Z_c сумма комплексных токов в точке n разветвления цепи, записанная в соответствии с I законом Кирхгофа:

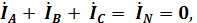
т. к. ток в нейтральном проводе I_N = 0. При этом напряжение, действующее

между нейтральными точками: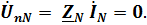

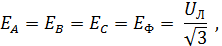Пренебрегая внутренним сопротивлением симметричного источника питания и учитывая, что ЭДС комплексное

напряжение, действующее между нейтральными точками системы, определяют исходя из выражения

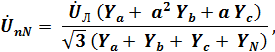
где 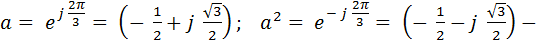поворотные множители (операторы).

Комплексные фазные напряжения потребителя электроэнергии находят из уравнений, составленных по II закону Кирхгофа для соответствующих замкнутых контуров системы (рис. 3.2):

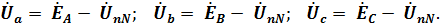
При этом комплексные фазные токи потребителя определяют по закону Ома для соответствующих участков цепи:

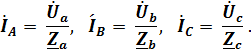
Комплексный ток в нейтральном проводе находят в соответствии с уравнением, составленным по I закону Кирхгофа для нейтральной точки n цепи: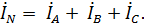

При симметричной нагрузке фазные напряжения: U_a = U_b = U_c = U_ф,

при этом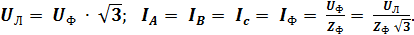

При обрыве нейтрального провода его полное сопротивление 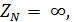а полная проводимость Y = 0.

При несимметричной нагрузке потребителя электроэнергии

(Z_a ≠ Z_b ≠ Z_c) на векторной диаграмме происходит смещение нейтральной точки ппотребителя относительно нейтральной точки N источника, что приводит к перекосу фазных напряжений потребителя. В результате на одних фазах потребителя напряжение будет больше, чем на других, что во многих случаях недопустимо, в частности при питании осветительной нагрузки, когда одни осветительные приборы находятся под напряжением, меньшим номинального, а другие − под напряжением, большим номинального, что приводит к преждевременному выходу приборов из строя. Поэтому в цепи нейтрального провода недопустимо наличие различного рода предохранителей и выключателей.

Трёхфазная четырёхпроводная система обеспечивает потребителя электроэнергии симметричным питанием. При этом активная, реактивная и полная мощности могут быть определены по следующим формулам с учётом знака реактивных сопротивлений:

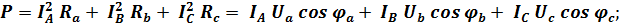
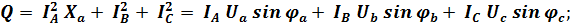
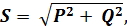
где 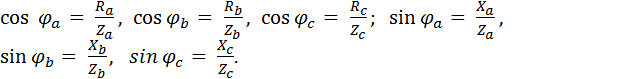При симметричной нагрузке эти формулы приводятся к виду:

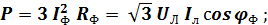
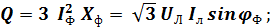
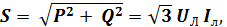
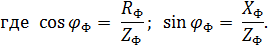
Литература. ГОСТ Р 52002 – 2003;[2] с. 107 − 119;

[3] с. 123 – 144; [4] с. 211 – 219, [5] с. 41 − 43.

Примеры решения

Задача № 1

Трёхфазный потребитель электроэнергии с активными и реактивными сопротивлениями

R₁ = 10 Oм, R₂ = R₃ = 5Oм и

X_L = X_C = 5 Oм фаз соединён «треугольником» (рис 3.3) и включён в трёхфазную сеть с линейным напряжением

U_Л = 100 В при симметричном питании. Определить:

1. Показания амперметра А при отключении (обрыве) линейного провода С (выключатель В разомкнут); 2. Фазные I_Ф и линейные I_Л токи, а также активную Р, реактивную Q и полную S мощности каждой фазы и всей электрической цепи (при замкнутом выключателе В ). Построить векторную диаграмму токов и напряжений.

Решение. Полное сопротивление параллельного участка цепи при обрыве линейного провода

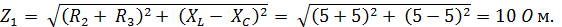
Т. к. реактивные сопротивления Х_L = X_C, то в цепи возникает резонанс напряжений, и она ведёт себя как активное сопротивление (Z₁ = R = 10 Oм).

Общее сопротивление цепи при обрыве линейного провода:

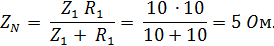
Показание амперметра при обрыве линейного провода С:

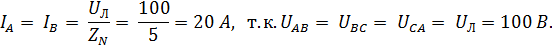
Фазные токи потребителя при замкнутом выключателе В:

>

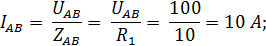
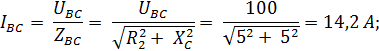
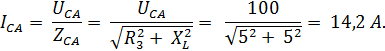
Векторная диаграмма токов и напряжений с учётом характера нагрузки представлена на рис 3.4.

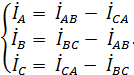
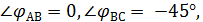− вектор тока опережает вектор напряжения,

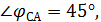− вектор тока отстаёт от вектора напряжения.

Составляющие фазных токов:

активные: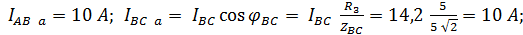

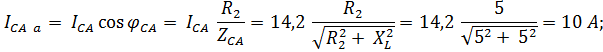
реактивные: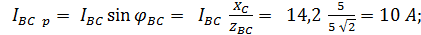

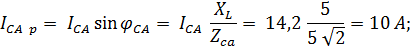
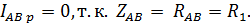
Линейные токи потребителя электроэнергии определяют исходя из векторной диаграммы (рис. 3.4):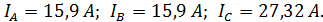

Мощности фаз потребителя:

активные: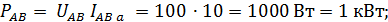

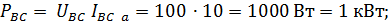
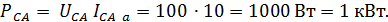
реактивные: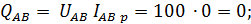

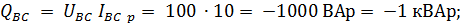
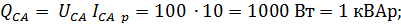
где знак минус указывает на ёмкостный характер мощности.

Полные мощности фаз потребителя:

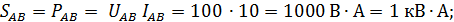
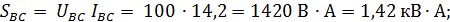
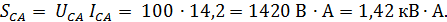
Мощности всей цепи:

активная: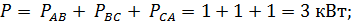

реактивная: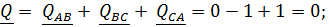

полная: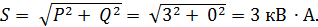

Рекомендуемая литература

1. ГОСТ Р 52002 – 2003 «Электротехника. Термины и определения основных понятий»

2. Немцов. М.В. Электротехника и электроника: учебник для вузов. –

М.: Высшая школа, 2007. – 560с.

3. Иванов И. И., Соловьёв Г. И. Электротехника: учебное пособие. – 6- е изд. – СПб.; М.; Краснодар: Лань, 2009. – 496 с.

4. Рекус Г. Г., Белоусов А. И. Сборник задач и упражнений по электротехнике и основам электроники: учебное пособие. – 2- е изд., перераб. − М.: Высшая школа, 2001. – 415 с.

5. Боровских С. М., Дорофеева И. С., Кропачева Л. П. Электротехника:

лабораторный практикум. – Пермь: ФГОУ ВПО «Пермская ГСХА»,

2011. – 66 с.

1 23

Дата добавления: 2017-11-21; просмотров: 8722;